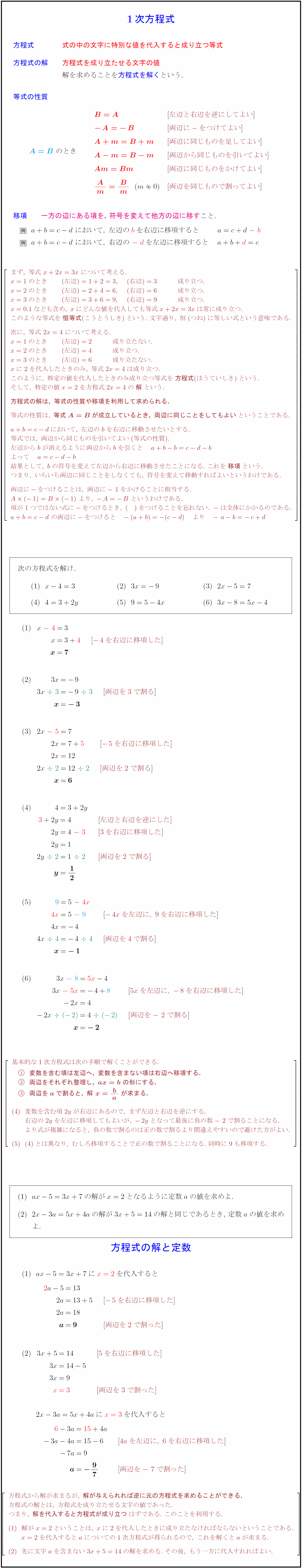
方程式 式の中の文字に特別な値を代入すると成り立つ等式 方程式の解 方程式を成り立たせる文字の値 解を求めることを方程式を解くという. 等式の性質 ${A=B\ のとき 左辺と右辺を逆にしてよい両辺に-をつけてよい}{両辺に同じものを足してよい}両辺から同じものを引いてよい両辺に同じものをかけてよい{両辺を同じもので割ってよい移項{一方の辺にある項を,\ 符号を変えて他方の辺に移すこと. まず,\ 等式\ x+2x=3x\ について考える. x=1のとき (左辺)=1+2=3, (右辺)=3 成り立つ. x=2のとき (左辺)=2+4=6, (右辺)=6 成り立つ. x=3のとき (左辺)=3+6=9, (右辺)=9 成り立つ. x=0.1なども含め,\ xにどんな値を代入しても等式x+2x=3xは常に成り立つ. このような等式を{恒等式}(こうとうしき)という.\ 文字通り,\ 恒(つね)に等しい式という意味である. 次に,\ 等式\ 2x=4\ について考える. x=1のとき (左辺)=2 成り立たない. x=2のとき (左辺)=4 成り立つ. x=3のとき (左辺)=6 成り立たない. xに2を代入したときのみ,\ 等式2x=4は成り立つ. このように,\ 特定の値を代入したときのみ成り立つ等式を{方程式}(ほうていしき)という. そして,\ 特定の値x=2を方程式2x=4の{解}という. {方程式の解は,\ 等式の性質や移項を利用して求められる.} 等式の性質は,\ {等式A=Bが成立しているとき,\ 両辺に同じことをしてもよい}ということである. a+b=c-dにおいて,\ 左辺のbを右辺に移動させたいとする. 等式では,\ 両辺から同じものを引いてよい(等式の性質). 左辺からbが消えるように両辺からbを引くと a+b-b=c-d-b よって a=c-d-b 結果として,\ bの符号を変えて左辺から右辺に移動させたことになる.\ これを{移項}という. つまり,\ いちいち両辺に同じことをしなくても,\ 符号を変えて移動すればよいというわけである. 両辺に-をつけることは,\ 両辺に-1をかけることに相当する. A(-1)=B(-1)\ より,\ -A=-B\ というわけである. 項が1つではない式に-をつけるとき,\ ( )をつけることを忘れない.\ -は全体にかかるのである. a+b=c-d\ の両辺に-をつけると -(a+b)=-(c-d) より -a-b=-c+d 基本的な1次方程式は次の手順で解くことができる. {変数を含む項は左辺へ,\ 変数を含まない項は右辺へ移項する.} {両辺をそれぞれ整理し,\ ax=b\ の形にする.} {両辺をaで割ると,\ 解\ x= ba\ が求まる.} 変数を含む項2yが右辺にあるので,\ まず左辺と右辺を逆にする. 右辺の2yを左辺に移項してもよいが,\ -2yとなって最後に負の数-2で割ることになる. より式が複雑になると,\ 負の数で割るのは正の数で割るより間違えやすいので避けた方がよい. とは異なり,\ むしろ移項することで正の数で割ることになる.\ 同時に9も移項する. 方程式から解が求まるが,\ {解が与えられれば逆に元の方程式を求めることができる.} 方程式の解とは,\ 方程式を成り立たせる文字の値であった. つまり,\ {解を代入すると方程式が成り立つ}はずである.\ このことを利用する. 解がx=2ということは,\ xに2を代入したときに成り立たなければならないということである. x=2を代入するとaについての1次方程式が得られるので,\ これを解くとaが求まる. 先に文字aを含まない3x+5=14の解を求める.\ その後,\ もう一方に代入すれればよい.

