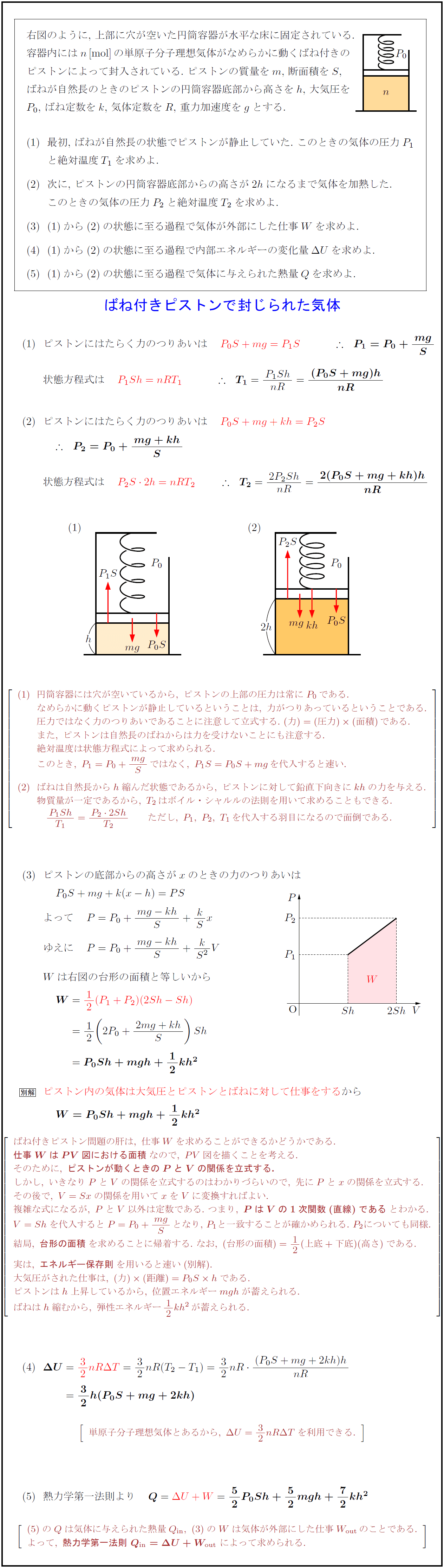
右図のように, 上部に穴が空いた円筒容器が水平な床に固定されている.
容器内には n [mol] の単原子分子理想気体がなめらかに動くばね付きの
ピストンによって封入されている. ピストンの質量を m, 断面積を S,
ばねが自然長のときのピストンの円筒容器底部から高さを h, 大気圧を
P₀, ばね定数を k, 気体定数を R, 重力加速度を g とする.
(1) 最初, ばねが自然長の状態でピストンが静止していた. このときの気体の圧力 P₁
と絶対温度 T₁ を求めよ.
(2) 次に, ピストンの円筒容器底部からの高さが 2h になるまで気体を加熱した.
このときの気体の圧力 P₂ と絶対温度 T₂ を求めよ.
(3) (1)から(2)の状態に至る過程で気体が外部にした仕事 W を求めよ.
(4) (1)から(2)の状態に至る過程で内部エネルギーの変化量 ΔU を求めよ.
(5) (1)から(2)の状態に至る過程で気体に与えられた熱量 Q を求めよ.
――――
ばね付きピストンで封じられた気体
(1) ピストンにはたらく力のつりあいは P₀S + mg = P₁S ∴ P₁ = P₀ + mg/S
状態方程式は P₁S h = n R T₁ ∴ T₁ = P₁ S h/(n R) = ( (P₀ S + m g) h )/(n R)
(2) ピストンにはたらく力のつりあいは P₀S + mg + k h = P₂S
∴ P₂ = P₀ + (m g + k h)/S
状態方程式は P₂ S · 2h = n R T₂ ∴ T₂ = 2 P₂ S h/(n R) = 2 (P₀ S + m g + k h) h/(n R)
[図示部分は省略せずに原文順のまま残しています]
(1) 円筒容器には穴が空いているから, ピストンの上部の圧力は常に P₀ である.
なめらかに動くピストンが静止しているということは, 力がつりあっているということである.
圧力ではなく力のつりあいであることに注意して立式する. (力) = (圧力) × (面積) である.
また, ピストンは自然長のばねからは力を受けないことにも注意する.
絶対温度は状態方程式によって求められる.
このとき, P₁ = P₀ + mg/S ではなく, P₁S = P₀S + mg を代入すると速い.
(2) ばねは自然長から h 縮んだ状態であるから, ピストンに対して鉛直下向きに k h の力を与える.
物質量が一定であるから, T₂ はボイル・シャルルの法則を用いて求めることもできる.
P₁ S h / T₁ = P₂ · 2 S h / T₂ ただし, P₁, P₂, T₁ を代入する羽目になるので面倒である.
(3) ピストンの底部からの高さが x のときの力のつりあいは
P₀S + m g + k(x − h) = P S
よって P = P₀ + (m g − k h)/S + (k/S) x
ゆえに P = P₀ + (m g − k h)/S + k/S² · V
W は右図の台形の面積と等しいから
W = 1/2 (P₁ + P₂) (2 S h − S h)
= 1/2 ( 2 P₀ + (2 m g + k h)/S ) S h
= P₀ S h + m g h + 1/2 k h²
別解 ピストン内の気体は大気圧とピストンとばねに対して仕事をするから
W = P₀ S h + m g h + 1/2 k h²
[PV 図の説明は原文順のまま]
ばね付きピストン問題の肝は, 仕事 W を求めることができるかどうかである.
仕事 W は PV 図における面積なので, PV 図を描くことを考える.
そのために, ピストンが動くときの P と V の関係を立式する.
しかし, いきなり P と V の関係を立式するのはわかりづらいので, 先に P と x の関係を立式する.
その後で, V = S x の関係を用いて x を V に変換すればよい.
複雑な式になるが, P と V 以外は定数である. つまり, P は V の 1 次関数(直線)であるとわかる.
V = S h を代入すると P = P₀ + m g/S となり, P₁ と一致することが確かめられる. P₂ についても同様.
結局, 台形の面積を求めることに帰着する. なお, (台形の面積) = 1/2 (上底 + 下底)(高さ) である.
実は, エネルギー保存則を用いると速い(別解).
大気圧がされた仕事は, (力) × (距離) = P₀ S × h である.
ピストンは h 上昇しているから, 位置エネルギー m g h が蓄えられる.
ばねは h 縮むから, 弾性エネルギー 1/2 k h² が蓄えられる.
(4) ΔU = 3/2 n R ΔT = 3/2 n R (T₂ − T₁) = 3/2 n R · ( (P₀ S + m g + 2 k h) h )/(n R)
= 3/2 h (P₀ S + m g + 2 k h)
単原子分子理想気体とあるから, ΔU = 3/2 n R ΔT を利用できる.
(5) 熱力学第一法則より Q = ΔU + W = 5/2 P₀ S h + 5/2 m g h + 7/2 k h²
(5)の Q は気体に与えられた熱量 Q_in, (3)の W は気体が外部にした仕事 W_out のことである.
よって, 熱力学第一法則 Q_in = ΔU + W_out によって求められる.

