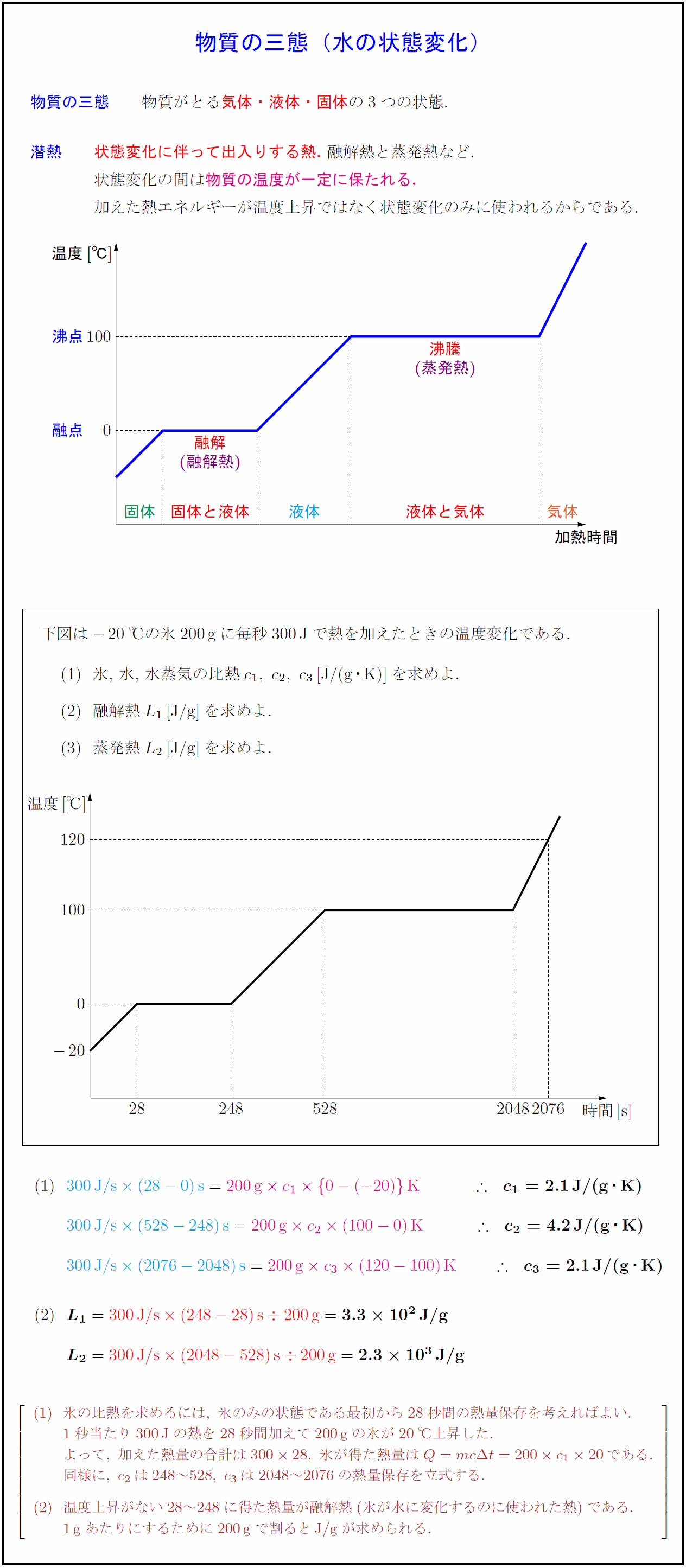
物質の三態 物質がとる気体・液体・固体の3つの状態. 潜熱 状態変化に伴って出入りする熱.\ 融解熱と蒸発熱など. 状態変化の間は物質の温度が一定に保たれる. 加えた熱エネルギーが温度上昇ではなく状態変化のみに使われるからである.加熱時間温度融点\ 0] {沸点100] {融解} (融解熱)} {沸騰} 蒸発熱) 下図は$-20$℃の氷200gに毎秒300Jで熱を加えたときの温度変化である. 氷,\ 水,\ 水蒸気の比熱$c₁,\ c₂,\ c₃$[J/(g$・$K)]を求めよ. 融解熱$L₁$[J/g]を求めよ. 蒸発熱$L₂$[J/g]を求めよ. 氷の比熱を求めるには,\ 氷のみの状態である最初から28秒間の熱量保存を考えればよい. 1秒当たり300J}の熱を28秒間加えて200g}の氷が20℃上昇した. よって,\ 加えた熱量の合計は30028,\ 氷が得た熱量はQ=mcΔ t=200 c₁20である. 同様に,\ c₂は248~528,\ c₃は2048~2076の熱量保存を立式する. 温度上昇がない28~248に得た熱量が融解熱(氷が水に変化するのに使われた熱)である. 1g}あたりにするために200g}で割るとJ/g}が求められる.

