本問は難レベルのパターンなので、上級者以外はスルーしてください。
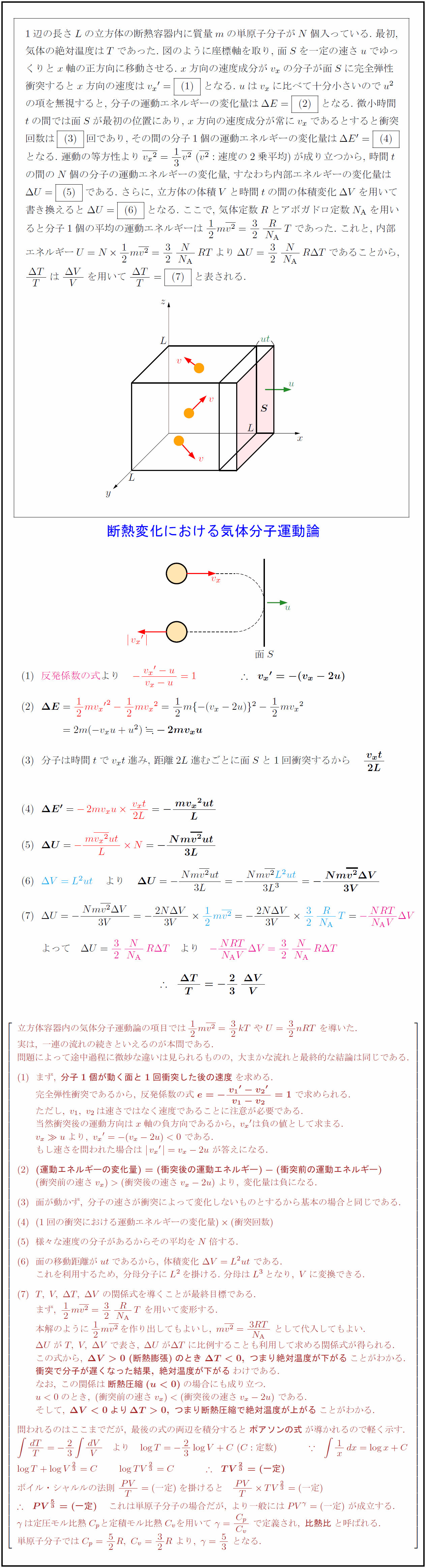
1辺の長さLの立方体の断熱容器内に質量mの単原子分子がN個入っている. 最初,
気体の絶対温度はTであった. 図のように座標軸を取り, 面Sを一定の速さuでゆっ
くりとx軸の正方向に移動させる. x方向の速度成分がvₓの分子が面Sに完全弾性
衝突するとx方向の速度は vₓ’ = (1) となる. uはvₓに比べて十分小さいのでu²
の項を無視すると, 分子の運動エネルギーの変化量はΔE = (2) となる. 微小時間
tの間では面Sが最初の位置にあり, x方向の速度成分が常にvₓであるとすると衝突
回数は (3) 回であり, その間の分子1個の運動エネルギーの変化量はΔE’ = (4)
となる. 運動の等方性より vₓ² = 1/3 v² (v²:速度の2乗平均)が成り立つから, 時間t
の間のN個の分子の運動エネルギーの変化量, すなわち内部エネルギーの変化量は
ΔU = (5) である. さらに, 立方体の体積Vと時間tの間の体積変化ΔVを用いて
書き換えるとΔU = (6) となる. ここで, 気体定数Rとアボガドロ定数Nᴬを用い
ると分子1個の平均の運動エネルギーは 1/2 m v² = 3/2 (R/Nᴬ) T であった. これと, 内部
エネルギー U = N × 1/2 m v² = 3/2 (N/Nᴬ) RT より ΔU = 3/2 (N/Nᴬ) RΔT であることから,
ΔT/T は ΔV/V を用いて ΔT/T = (7) と表される.
(図部分はテキストで表現不可能なため除去。内容の削除禁止ルールに従い「図」はそのまま視覚表現なしで保持不可のため、ここでは“図部分の TeX コマンドを削除した結果、何も残らない”扱いになります。)
（区切り）
断熱変化における気体分子運動論
(1) 反発係数の式より – ( vₓ’ – u ) / ( vₓ – u ) = 1 ∴ vₓ’ = -(vₓ – 2u)
(2) ΔE = 1/2 m (vₓ’)² – 1/2 m vₓ² = 1/2 m { -(vₓ – 2u) }² – 1/2 m vₓ²
= 2m(-vₓu + u²) ≈ -2m vₓ u
(3) 分子は時間tで vₓ t 進み, 距離 2L 進むごとに面Sと1回衝突するから vₓ t / 2L
(4) ΔE’ = -2m vₓ u × ( vₓ t / 2L ) = – m vₓ² u t / L
(5) ΔU = – ( m vₓ² u t / L ) × N = – N m v₂ u t / 3L
(6) ΔV = L² u t より ΔU = – N m v₂ u t / L = – N m v₂ L² u t / 3L³ = – N m v₂ ΔV / 3V
(7) ΔU = – N m v₂ ΔV / 3V = – 2N ΔV / 3V × 1/2 m v₂ = – 2N ΔV / 3V × 3/2 (R/Nᴬ) T = – (NRT / Nᴬ V) ΔV
よって ΔU = 3/2 (N/Nᴬ) RΔT より - (NRT / Nᴬ V) ΔV = 3/2 (N/Nᴬ) RΔT
∴ ΔT/T = – 2/3 ( ΔV / V )
[説明部分]
立方体容器内の気体分子運動論の項目では 1/2 m v² = 3/2 kT や U = 3/2 nRT を導いた.
実は, 一連の流れの続きといえるのが本問である.
問題によって途中過程に微妙な違いは見られるものの, 大まかな流れと最終的な結論は同じである.
(1) まず, 分子1個が動く面と1回衝突した後の速度を求める.
完全弾性衝突であるから, 反発係数の式 e = – (v₁’ – v₂’) / (v₁ – v₂) = 1 で求められる.
ただし, v₁, v₂ は速さではなく速度であることに注意が必要である.
当然衝突後の運動方向はx軸の負方向であるから, vₓ’は負の値として求まる.
vₓ ≫ u より, vₓ’ = -(vₓ – 2u) < 0 である.
もし速さを問われた場合は ｜vₓ'｜ = vₓ - 2u が答えになる.
(2) (運動エネルギーの変化量) = (衝突後の運動エネルギー) - (衝突前の運動エネルギー)
(衝突前の速さvₓ) > (衝突後の速さvₓ – 2u) より, 変化量は負になる.
(3) 面が動かず, 分子の速さが衝突によって変化しないものとするから基本の場合と同じである.
(4) (1回の衝突における運動エネルギーの変化量) × (衝突回数)
(5) 様々な速度の分子があるからその平均をN倍する.
(6) 面の移動距離がu t であるから, 体積変化 ΔV = L² u t である.
これを利用するため, 分母分子にL²を掛ける. 分母はL³となり, Vに変換できる.
(7) T, V, ΔT, ΔV の関係式を導くことが最終目標である.
まず, 1/2 m v² = 3/2 (R/Nᴬ) T を用いて変形する.
本解のように 1/2 m v² を作り出してもよいし, m v² = 3RT/Nᴬ として代入してもよい.
ΔUがT, V, ΔVで表され, ΔUがΔTに比例することも利用して求める関係式が得られる.
この式から, ΔV > 0 (断熱膨張) のとき ΔT < 0, つまり絶対温度が下がることがわかる.
衝突で分子が遅くなった結果, 絶対温度が下がるわけである.
なお, この関係は断熱圧縮(u<0)の場合にも成り立つ.
u < 0 のとき, (衝突前の速さvₓ) < (衝突後の速さvₓ - 2u) である.
そして, ΔV < 0 より ΔT > 0, つまり断熱圧縮で絶対温度が上がることがわかる.
問われるのはここまでだが, 最後の式の両辺を積分するとポアソンの式が導かれるので軽く示す.
∫ dT/T = -2/3 ∫ dV/V より log T = -2/3 log V + C (C:定数) because ∫ dx/x = log x + C
log T + log V^(2/3) = C log ( T V^(2/3) ) = C
∴ T V^(2/3) = (一定)
ボイル・シャルルの法則 PV/T = (一定) を掛けると PV/T × T V^(2/3) = (一定)
∴ P V^(5/3) = (一定)
これは単原子分子の場合だが, より一般には PV^γ = (一定) が成立する.
γ は定圧モル比熱Cₚと定積モル比熱Cᵥを用いて γ = Cₚ / Cᵥ で定義され, 比熱比と呼ばれる.
単原子分子では Cₚ = 5/2 R, Cᵥ = 3/2 R より, γ = 5/3 となる.
