以下はGeoGebraによる作図です。自分でスライダーを動かしてみてください。自動再生もできます。
準円が漸近線をまたぐ瞬間に接点の位置が左から右、右から左に入れ替わることを確認してください。
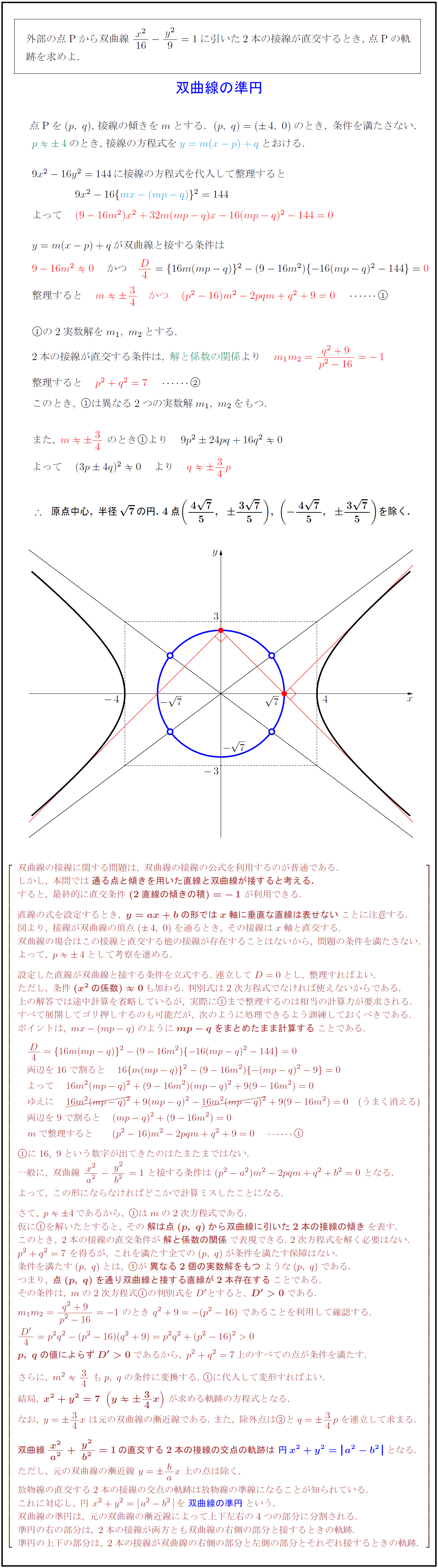
外部の点Pから双曲線\ ${x²}{16}-{y²}{9}=1$に引いた2本の接線が直交するとき,\ 点Pの軌 跡を求めよ. 点Pを$(p,\ q)$,\ 接線の傾きを$m$とする.$(p,\ q)=(4,\ 0)のとき,\ 条件を満たさない.$ $p4}$のとき,\ 接線の方程式を$y=m(x-p)+q}$とおける. $9x²-16y²=144に接線の方程式を代入して整理すると$ $ 9x²-16{mx-(mp-q)²=144$ $よって (9-16m²)x²+32m(mp-q)x-16(mp-q)²-144=0}$ $y=m(x-p)+qが楕円と接する条件は$ $9-16m²0} かつ {D}{4={16m(mp-q)}²-(9-16m²){-16(mp-q)²-144}=0}$ $整理すると m34 かつ (p²-16)m²-2pqm+q²+9=0} $ $の2実数解をm₁,\ m₂とする.$ $2本の接線が直交する条件は,\ 解と係数の関係}より m₁m₂={q²+9}{p²-16}=-1}$ $整理すると p²+q²=7} $ $このとき,\ は異なる2つの実数解m₁,\ m₂をもつ.$ $また,\ m34}\ のときより 9p²24pq+16q²0$ $よって (3p4q)²0 より q34p}$ .95}{${原点中心,\ 半径7の円.\ 4点({47}{5},{37}{5}),\ (-{47}{5},{37}{5})を除く.}$ 双曲線の接線に関する問題は,\ 双曲線の接線の公式を利用するのが普通である. しかし,\ 本問では{通る点と傾きを用いた直線と双曲線が接すると考える.} すると,\ 最終的に直交条件\ {(2直線の傾きの積)=-1}\ が利用できる. 直線の式を設定するとき,\ {y=ax+bの形ではx軸に垂直な直線は表せない}ことに注意する. 図より,\ 接線が双曲線の頂点(4,\ 0)を通るとき,\ その接線はx軸と直交する. 双曲線の場合はこの接線と直交する他の接線が存在することはないから,\ 問題の条件を満たさない. よって,\ p4として考察を進める. 設定した直線が楕円と接する条件を立式する.\ 連立してD=0とし,\ 整理すればよい. ただし,\ 条件{(x²の係数)0}も加わる.\ 判別式は2次方程式でなければ使えないからである.\ 上の解答では途中計算を省略しているが,\ 実際にまで整理するのは相当の計算力が要求される. すべて展開してゴリ押しするのも可能だが,\ 次のように処理できるよう訓練しておくべきである. ポイントは,\ mx-(mp-q)のように{mp-qをまとめたまま計算する}ことである. {D}{4}={16m(mp-q)}²-(9-16m²){-16(mp-q)²-144}=0 両辺を16で割ると 16{m(mp-q)}²-(9-16m²){-(mp-q)²-9}=0 よって 16m²(mp-q)²+(9-16m²)(mp-q)²+9(9-16m²)=0 ゆえに 16m²(mp-q)²}+9(mp-q)²-16m²(mp-q)²}+9(9-16m²)=0\ (うまく消える) 両辺を9で割ると (mp-q)²+(9-16m²)=0 mで整理すると (p²-16)m²-2pqm+q²+9=0 に16,\ 9という数字が出てきたのはたまたまではない. 一般に,\ 双曲線\ {x²}{a²}-{y²}{b²}=1\ と接する条件は\ (p²-a²)m²-2pqm+q²+b²=0\ となる. よって,\ この形にならなければどこかで計算ミスしたことになる. さて,\ p4であるから,\ はmの2次方程式である. 仮にを解いたとすると,\ その{解は点(p,\ q)から双曲線に引いた2本の接線の傾き}を表す. このとき,\ 2本の接線の直交条件が{解と係数の関係}で表現できる.\ 2次方程式を解く必要はない. p²+q²=7\ を得るが,\ これを満たす全ての(p,\ q)が条件を満たす保障はない. 条件を満たす(p,\ q)とは,\ が{異なる2個の実数解をもつ}ような(p,\ q)である. つまり,\ {点(p,\ q)を通り双曲線と接する直線が2本存在する}ことである. その条件は,\ mの2次方程式の判別式をD’とすると,\ {D’0}である. m₁m₂={q²+9}{p²-16}=-1\ のとき\ q²+9=-(p²-16)\ であることを利用して確認する. {D’}{4}=p²q²-(p²-16)(q²+9)=p²q²+(p²-16)²0 {p,\ qの値によらずD’0}であるから,\ p²+q²=7上のすべての点が条件を満たす. さらに,\ m²34\ もp,\ qの条件に変換する.\ に代入して変形すればよい. 結局,\ {x²+y²=7\ (y34x)}\ が求める軌跡の方程式となる. なお,\ y=34x\ は元の双曲線の漸近線である.\ また,\ 除外点はとq=34pを連立して求まる. {双曲線{x²}{a²}+{y²}{b²}=1の直交する2本の接線の交点の軌跡は\ 円x²+y²=a²-b²}となる. ただし,\ 元の双曲線の漸近線\ y= bax\ 上の点は除く. 放物線の直交する2本の接線の交点の軌跡は放物線の準線になることが知られている. これに対応し,\ 円\ x²+y²=a²-b²}を{双曲線の準円という. 双曲線の準円は,\ 元の双曲線の漸近線によって上下左右の4つの部分に分割される. 準円の右の部分は,\ 2本の接線が両方とも双曲線の右側の部分と接するときの軌跡. 準円の上下の部分は,\ 2本の接線が双曲線の右側の部分と左側の部分とそれぞれ接するときの軌跡.

