
2016年東京医科歯科大学入試の試験開始直後、第1問をみて「予想していた問題が出たあああ」と歓喜した受験生が少なからずいたであろう。

本問のテーマは
Perfect Number
日本語では「完全数」、受験数学において最も厨二病心をくすぐられる数学用語の一つである。
この年、どこかの大学で完全数の問題が出題されることが確実視されていたのだ。
その理由は後述するとして、先に完全数の歴史を振り返っておくとしよう。
完全数とメルセンヌ素数の発見の歴史
完全数の神秘的な性質は、古代ギリシャの時代から数学者達を魅了してきた。
完全数とは、「自分自身が自分自身を除く正の約数の和と完全に一致する自然数」である。
言い換えると、「正の約数の和が自分自身の2倍になる自然数」となる。
例えば、6=1+2+3(1+2+3+6=12)であるから、6は完全数である。
完全数を小さい順に並べると次のようになる。ご覧の通り、非常にレアな数である。
6 28 496 8128 33550336 ・・・・・・
「完全数」は、古代ギリシャの数学者・哲学者ピタゴラス(紀元前6世紀頃)によって名付けられたという。
The original uploader was Galilea at German Wikipedia., Public domain, via Wikimedia Commons
ピタゴラスは、紀元前580年頃、ギリシャのサモス島で誕生した。
若い頃にエジプトやバビロニアを旅しながら学び、当時の世界に存在した数学法則をすべて習得したピタゴラスは、あらゆる事象には数が内在し、宇宙のすべては人間の主観ではなく数の法則に従うのであり、数字と計算によって解明できるという思想を確立した。
「万物の根源は数である」
このような思想に基づき、40歳頃にクロトン(現在のイタリア)にて宇宙の真理を追究する「ピタゴラス教団」と呼ばれる宗教団体を設立した。
団員はピタゴラスを頂点に団結し、霊魂の不滅と輪廻と死後の応報を信じて様々な戒律の下に禁欲的、厳格な生活を送った。きわめて排他的で、教えや発見を外に漏らすことが禁じられた。ピタゴラスの死後でさえ、誓いを破った者が溺死させられたという。また、財産や研究結果の共有を原則としたため、死後100年後にはすでにピタゴラスの業績と弟子の業績を区別することが困難になっていた。
ピタゴラス教団は、宇宙の真理を追究する手段として数学、音楽、哲学、天文学を重んじた。
幾何学では、三角形の内角の和が180°であることの証明、正五角形の作図、1種類で平面を充填できる正多角形が正三角形・正方形・正六角形に限られることの証明、正多面体の発見などの功績を残した。
いわゆるピタゴラスの定理(三平方の定理)は、かつてはピタゴラスが発見したとされていたが、三平方の定理が描かれた紀元前2000年頃に栄えた古代バビロニア(現イラク)の粘土板が発見されるなど、現在はピタゴラス以前から知られており、ピタゴラスが古代ギリシャに広めたとの説が有力である。その証明は紀元前3世紀の数学者ユークリッドの『原論』において与えられた。
数論では、黄金数、無理数、三角数、長方形数、五角形数、六角形数を発見した。また、完全数や友愛数(自分自身を除いた約数の和が互いに他方と等しくなるような2数)を宗教的に崇拝し、友愛数の一対(220と284)を発見した。
音楽では、音程と数の比例を発見し、ピタゴラス音階の確立などの功績を残した。
音楽における調和の発見に基づき、惑星の運動の中にも比例と調和があり、音楽研究によって宇宙の全てを解明できると考えた。この「天球の音楽」と呼ばれるピタゴラス教団の宇宙観は、ケプラーの惑星運動の法則の発見やニュートンの万有引力の発見につながっていく。
紀元前500年頃、ピタゴラス教団は地域の有力者の協力も得て大きな影響力を持つようになっていたが、ある時この有力者が失脚し、かつて入団を希望したもののテストで落とされた人物によって扇動され暴徒と化した市民によってピタゴラスは殺害されたという。秘密主義故の批判も多かった教団への迫害がその後も続き、多くの弟子は国外移住を余儀なくされた。しかし、このことによりピタゴラス教団の数学が古代世界に広まることになった。
「数学理論の正しさは目上の者の意見ではなく論理で決まる」「数と自然界のつながりを探求する」というピタゴラスの精神は、彼が後世に残した最大の貢献であり、これからも永遠に生き続ける。
その完全数に関する最初の成果は、紀元前3世紀頃ユークリッドによって与えられた。
ユークリッドは、『原論』(第9巻命題36)で「 2n−1 が素数ならば、2n-1(2n−1) は完全数である」を証明した。2n−1 で表される数をメルセンヌ数といい、素数となるメルセンヌ数をメルセンヌ素数という。つまり、メルセンヌ素数を発見すると自動的に偶数の完全数も発見される。
Photograph taken by Mark A. Wilson (Wilson44691, Department of Geology, The College of Wooster).[1], CC BY-SA 4.0, via Wikimedia Commons
エウクレイデス(英語名ユークリッド)は、歴史上最も著名な数学者の一人であるにもかかわらず、その生涯については紀元前3世紀頃に存在したという以外にほとんど何もわかっていない。
古代エジプトのギリシャ系数学者・天文学者とされ、数学史上最も重要な著作の1つ『原論(ストイケイア)』を編纂した。『原論』の内容の多くはユークリッドが発見したものではないが、ピタゴラス学派などそれ以前の数学者達の業績にユークリッド自身が現代数学にも通用するレベルの厳密な証明を追加して体系的にまとめ上げたものであり、論証的学問としてその地位が確立された古代ギリシャ数学の集大成である。20世紀初頭まで標準的な数学(特に幾何学)の教科書として使われ続けたため、聖書に次いで世界中で読まれてきた本とも評される。
原論の内容は、「幾何学」「比例論」「数論」「無理数」からなる。
「幾何学」では、点や直線が何であるかを定義し、議論の最低限の前提である極少数の「公理(公準)」を元に命題を証明して「定理」を得るという正に現代数学と同じ考え方で体系化されている。
ユークリッドが「幾何学」で規定した公準(現代数学の公理)が以下の5つである。
- 点と点を直線で結ぶ事ができる。
- 線分は両側に延長して直線にできる。
- 1点を中心にして任意の半径の円を描く事ができる。
- 全ての直角は等しい。
- 1つの直線が2つの直線に交わり、同じ側の内角の和が2つの直角より小さいならば、この2つの直線は限りなく延長されると、2つの直角より小さい角のある側において交わる。
この5つの公準のうち、5番目のいわゆる「平行線公準」が他の4つに比べてやたらと複雑であったために、2000年もの間その必要性が疑問視されてきた。
19世紀になってようやく、他の4つの公準は満たすが平行線公準を満たさない新たな幾何学(非ユークリッド幾何学という)を構成できることがわかった。つまり、ユークリッドの幾何学においては平行線公準が必須というわけである。ユークリッドは正しかったのだ。
「数論」についての記述の中には、素数が無限に存在することの証明、ユークリッドの補題(素因数分解の一意性の証明に利用)、ユークリッドの互除法(2数の最大公約数を求める)、完全数とメルセンヌ数の関係など、高校数学・受験数学において馴染みが深いものも多い。
他にも、『図形分割論』『光学』『球面天文学』『音楽原論』『透視図法』『円錐曲線論』などの著作を残したとされている。
逆の「すべての偶数の完全数が 2n-1(2n−1) の形で表せるか」は長らく未解決だったが、ユークリッドの証明から2000年近く経過した18世紀になってようやく18世紀最大の数学者レオンハルト・オイラー(スイス)によって肯定的に解決された。メルセンヌ素数 2n−1 と偶数の完全数 2n-1(2n−1) が1対1で対応することが示されたわけである。
Jakob Emanuel Handmann, Public domain, via Wikimedia Commons
レオンハルト・オイラーは、歴史上最も偉大な数学者の1人であり、18世紀最大の数学者である。
ニュートンが数学を自然界に応用し多くの科学的な実績を残していた18世紀初頭、オイラーはスイスのバーゼルで誕生した。
1720年、わずか13歳にしてバーゼル大学に入学して哲学を学んだが、スイスで有名な数学者一族ベルヌーイ家のヨハン・ベルヌーイに数学の才能を見い出された。1735年にバーゼル問題を解決したことで一目置かれる存在になる。
オイラーは、人間離れした計算力と記憶力で膨大な計算を暗算で行うことができた。8桁同士の掛け算を数秒、寝付けなかったときには100までの整数の6乗を暗算していたなど、伝説的エピソードに事欠かない。
数学のあらゆる分野に基礎から応用まで、さらには物理学にも膨大な業績を残した。オイラーの公式、オイラー定数、オイラー方程式、オイラー関数、オイラー予想、オイラー近似、一筆書きができる必要十分条件(オイラーグラフ)、オイラー線、オイラーの多面体公式、オイラーの運動方程式など、様々な分野で頻繁にオイラーの名が登場する。他の数学者の名を冠していても実はオイラーの貢献による業績も多い。また、π、sin、cos、i、e、Σ、y=f(x)、三角形の角Aの対辺のaなど現在世界中で使用されている記号を普及させた。さらには、幾何学で表現されていたニュートン力学を「ma=F」という現在の解析的表現に変更したのもオイラーである。当時まだ市民権を得られていなかった虚数iを積極的に活用してその有用性を広めた功績も大きい。数学者には珍しく、学生に研究成果を平易に解説することにも長けており、教育者としても優秀であった。
非常に温厚で性格で、膝の上で子守をしながら論文を執筆していたとされる。国家に対しても従順で、暦の作成、硬貨の鋳造、運河の設置、水道の設計、大砲の改良、航海表の作成など様々な問題を解決した。
悪環境やストレスから、30歳になる頃には片目を、60歳になる頃には両目を失明してしまうが、論文を書くペースは全盲になっても全く変わることはなく、1783年に76歳で亡くなるその日まで数学に没頭していたという。
オイラーは1年間に普通の数学者の一生分に相当する平均800ページもの論文を書いたため、人類史上最も多くの論文を書いた数学者である。オイラーの論文は5万ページを超える全集にまとめられて1911年から刊行され続けているが、その全集は100年以上たった今日でも完結していない。
また、一般に「 2n−1 が素数ならばnが素数」が成り立つ(大学入試標準レベル)。この対偶は「nが素数でないならば 2n−1 が素数でない」であるから、偶数の完全数の探索はnが素数の場合のみを考えればよい。ただし、逆の「nが素数ならば 2n−1 が素数」は成り立たない。
以上から、偶数の完全数の探索は「nが素数のとき 2n−1 が素数になるか」という問題に帰着する。
以下のページにユークリッドの証明(易)とオイラーの証明(難)と「 2n−1 が素数ならばnが素数(標準)」の証明が示してある。
古代ギリシャの数学者達が発見できた完全数は、4番目の8128までであった。
その後、5番目が発見されるまでに1700年以上もの歳月を要した。
5番目 212(213−1) = 33550336 (1456年)
6番目 216(217−1) = 8589869056 (1588年)
7番目 218(219−1) = 137438691328 (1588年)
結局、オイラーが登場するまでの約2000年間で発見された完全数は、わずか3個にとどまった。
1772年、オイラーは 231−1 が素数であることを確認した。8番目の完全数の発見である。
8番目 230(231−1) = 2305843008139952128
次に発見されたのは、9番目ではなく12番目の完全数であった。
そもそも 2n−1 がメルセンヌ数と呼ばれるのは、1644年にマラン・メルセンヌ(フランス)が「 nが素数のとき 2n−1 が素数になるのは、n≦257 では n=2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257 の11個の場合に限られる」と予想したことに由来する。
オイラーによって n=31 が示されたので、次は n=67 と n=127 の場合の証明が数学者の目標になったのである。
エドゥアール・リュカ(フランス)は、1857年15歳のときにリュカ・テストと呼ばれる効率的な素数判定法を考案し、n=67とn=127の場合の判定を開始した。効率的とはいっても想像を絶する計算量が必要になることには変わりない。267−1 が素数でないことと、2127−1=170141183460469231731687303715884105727 (39桁)が素数であることを確めることができたのは、19年後の1876年になってからであった。77桁の完全数が発見されたわけだが、12番目であることは後に判明する。結局、コンピューターが登場するまでこれより大きい完全数は発見されず、n=127の場合が手計算で発見された最大の完全数であり続けるだろう。
その後リュカ・テストが改良され、メルセンヌの予想になかった n=61, 89, 107 のときにも素数になることが判明した(9, 10, 11番目の完全数の発見)。1883年、1911年、1914年のことである。
リュカ・テストでは 267−1 が素数ではないことがわかるが、具体的にどんな因数をもつかまではわからない。フランク・ネルソン・コール(アメリカ)は因数を求めるため、隙間時間に3年間計算し続けた。
1903年、ニューヨークで開かれたアメリカ数学界の会議で黒板の前に立ったコールは、267−1 の値、つまり147573952589676412927 を注意深く書いた。次に黒板の前の別の場所へ移動し、193707721 × 761838257287 と書いて、手計算を開始した。一言も発しないまま約1時間かけて両者の値が等しいことを示し、コールは自分の席に戻った。その後、少し間を置いてから拍手が沸き起こったという。
1922年には n=257 が合成数となることが確認され、メルセンヌの予想は2つ誤り、3つ不足という結果で完全に決着した。
1952年、ついにコンピューターが登場し、13番目から17番目の完全数が一気に発見される。
以降、コンピューターの計算能力の上昇に伴い、1~3年に1個くらいのペースで巨大メルセンヌ素数が発見され続けている。
1996年には、メルセンヌ素数探索のための分散コンピューティングプロジェクト「GIMPS」が発足した。35番目以降の完全数の発見はすべてGIMPSによる。
2021年8月現在、51個の完全数が発見されており、最大は 282589932(282589933−1) という4972万4095桁の数である。
完全数については、2022年の時点でも「偶数の完全数は無数に存在するか?」「奇数の完全数は存在するか?」は未解決である。仮に奇数の完全数が存在するとすれば、少なくとも10¹⁵⁰⁰より大きい数であることがわかっている。
参考文献 完全数 – Wikipedia
2016年(平成28年)は奇跡の年
2016年正月、Twitter上では毎年の恒例となった新年の西暦の数字遊びがかつてない盛り上がりを見せていた。
「2016という数はこんな面白い性質をもつ」というつぶやきが競い合うようにツイートされていたのである。
その中でも特筆されたのは、西暦の2016と和暦の28がどちらも 2n-1(2n−1) で表される数という奇跡的な事実であった。しかも28は完全数である。

これはもう定められた宿命である
今年は完全数の問題が出る
2016年東京医科歯科大学医学部
2016年、あからさまに完全数の出題をしたのは東京医科歯科大学と浜松医科大学である。
浜松医科大学のほうは完全数のパターンそのままという問題だったので、ややマニアックな完全数の性質を証明する東京医科歯科大学医学部の問題を伝説の入試問題として認定する。問題を再掲。

(1)は、p²q型の完全数を求めるというもので、大学入試で散見される。標準レベル。
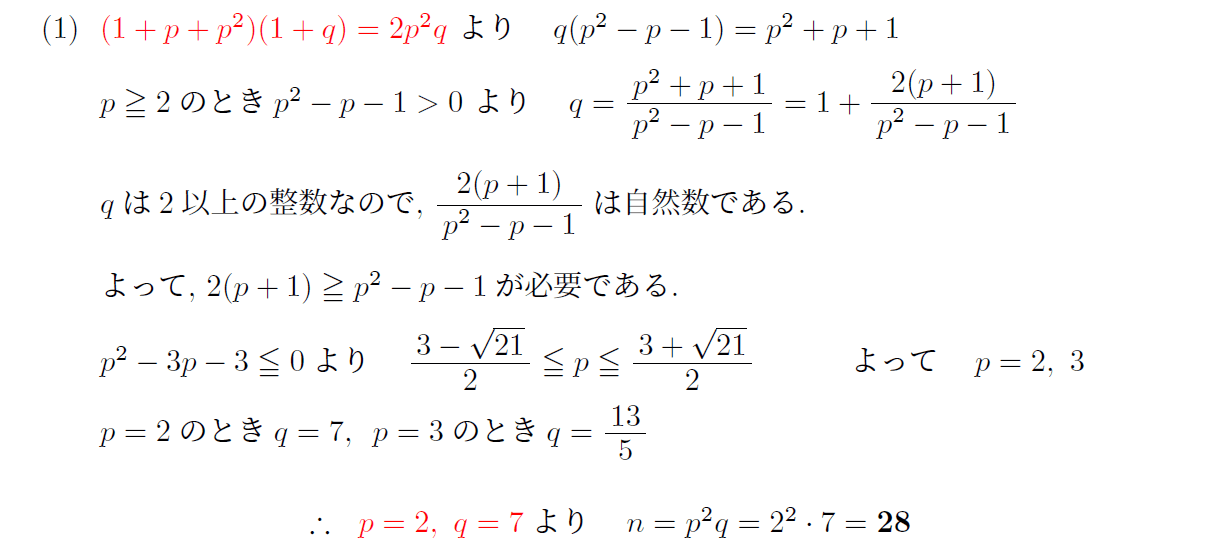
本問から、p²q型の完全数が28に限られることがわかる。
ちなみに、pq型の完全数は、(1+p)(1+q)=2pq より (p-1)(q-1)=2 であることから、6=2×3 のみであるとわかる。基本レベル。
(2)は、要は「n=2a-1が素数 ⇒ aが素数」を示せというものであり、これも大学入試で散見される。標準レベル。

(3)は、完全数についての知識を持っていなければ難しい。
事前の情報収集によって宿命の年であることを認識し、十分な対策を積んできていたならば圧倒的に有利になる。
医学部受験では、こういった情報収集能力も必要なのである。

「 S(n)≦2n のとき」とあるが、n=2a-1(2a-1) ならば S(n)≧2n なので、結局は「 S(n)=2n のとき」、つまりは「完全数のとき」となる。
結局、偶数の完全数の一の位は6か8であることがわかる。
2016の様々な性質
2016の他の代表的な特徴として、素因数分解すると 2016=2⁵×3²×7 のように1桁の素因数が3個現れることが挙げられる。
シンプルに素因数分解できるために問題作成に利用しやすく、2016年入試では2016という数が多くの大学で乱舞した。
また、3つの素因数の指数がすべて異なるというあからさまに約数の個数と総和を問うてくださいと言わんばかりの素因数分解であり、慶應義塾大学理工学部などで出題された。


正の約数の平均が自然数になるのは2004以来である。
今後素因数分解で1桁の素数の積となるのは、2025=3⁴×5²、 2048=2¹¹、2058=2×3×7³、2100=2²×3×5²×7 であるが、2016ほど約数の個数と総和を問うのに適切な年は 2160=2⁴×3³×5 まで待たなければならない。
28と2016は他にも面白い性質をもつので最後に解説つきで紹介しておく。
以下の性質は偶然ではなく、28と2016がいずれも 2n-1(2n−1) で表されることからくる必然である。






