
小中高常に成績はトップクラス、幼い頃より神童と崇め立てられ、エリート街道を突き進んできた東大受験生達がようやく辿り着いた最終決戦の場。
東京大学
すぐそこに夢にまで見た東大合格がある。これまでの努力がついに報われるときがやって来たのだ。
1980年代には毎年のように変更が行われるなど大混乱した大学受験制度であったが、1990年代にはセンター試験が始まって制度は安定し、受験数学・暗記数学という言葉も定着し、すでに東大合格のメソッドは確立されていた。
早い段階で高校数学の全範囲を終え、高校3年生の大部分をパターン問題・応用問題演習に費やす。塾の指導でも徹底した合理化・効率化が図られ、数十年分の過去問も解いてきた東大受験生達の準備に抜かりはない。
東大受験生 「2倍角・3倍角・半角・和積・積和公式は加法定理さえ覚えておけば全部そこから導ける。こんなの全部丸暗記している人は数学的センスがないよ。とにかく根幹となる加法定理だけは確実に暗記して、そこから導けるようにしておいた方が応用が利く。受験勉強はこうやって要領よくやることが大事だ。」
こうして迎えた本番である。
試験官 「始め!!!」
東大受験生 「よっしゃあああ、どんな問題でもかかってこい!!!」

東京大教授 「(第1問)では、加法定理を証明せよ」
東大受験生 「ぎゃあああああああああああああああ」
それはおそらく、試験開始直後の一瞬の出来事だったに違いない。
東京大学は、受験生のすべてを否定し、第1問でいきなり完璧な絶望を植えつけたのだ。
東大受験生であれば、仮に意識していなかったとしても受験勉強する過程で大抵の公式の証明方法が自然と身に付いているはずである。
しかし、加法定理の証明は恐ろしい盲点である。意表をつかれて血の気が引いた受験生が多数いたであろうことは容易に推測できる。
「公式は証明してから使うべき」という東大からのメッセージなのだろうか。あるいは、教科書の内容すら身に付いていない内に難しい問題集を解いている受験生に対する警告なのだろうか。
周りが並の受験生だったならば、「どうせ他の受験生もできないだろう」などと思えたのかもしれないが、ここは東京大学、最上位層の受験生ばかりである。
他の受験生には超易問、自分には超難問
最上位層が1点を争う東大入試においてこれがどれほど絶望的なことなのか。
全ては本質を見失い、教科書を疎かにしてきた自身の愚かさが招いた悲劇であった。
もっとも、終わってみれば出来は非常に悪かったらしいので(出来ていたのは2割?)、試験中に悲観する必要は全くなかったのだが。
本来、数学において証明が重要であるのは言うまでもない。
証明できない公式を使うということは、土台が不安定な橋を渡るような危険な行為である。一方で、受験は効率の良さが大事であり、いちいち厳密な証明を気にしていては受験勉強がはかどらないのも事実である。しかし、そのような効率重視の受験数学が蔓延することに危機感を感じた東大が、「学問としての数学」の軽視に対して一石を投じようとしたのかもしれない。
たったの一度でも入試で出題されたとなれば、そのインパクトは絶大である。この年以降、東大受験生は公式や定理を証明込みで丁寧に学習せざるを得なくなった。
解答

単なる三角関数の加法定理の証明かと思いきや、意外と奥が深い問題である。
まず、(1)(2)ともに「一般角」で考えなければならないことに注意する。つまり、(1)で直角三角形を用いた定義を述べてはならない。
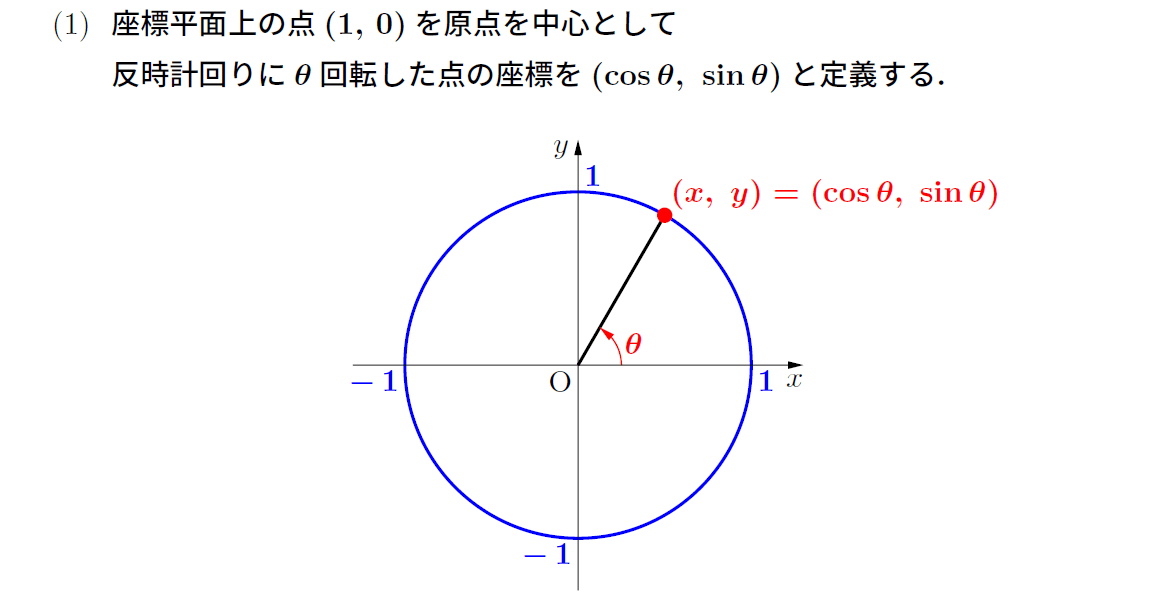
また、(2)では「(1)で述べた定義にもとづき」証明しなければならない。
三角関数の定義については大学で高校とは異なる定義を学習するが、(1)で述べた定義以外の定義にもとづく方法で証明してはならないわけである。
さらに、回転行列(1999年当時の理系は学習)や複素数の積を安易に利用すると、高校数学ではそれ自体が加法定理から導かれているため、循環論法に陥る危険性が高い。
結局、教科書に載っている2点間の距離の公式(三平方の定理)を利用する方法が最も安全で確実である。さすがに中学で学習する三平方の定理は自明としてよいだろう。
以下では、いわゆる負角の公式や余角の公式も定義に基づき導いている。


プトレマイオスと加法定理
最後に三角関数の加法定理の起源を紹介しておく。
これは、2世紀頃の古代ギリシャの数学者・天文学者のプトレマイオスの著書『アルマゲスト』にまで遡ることができる。
プトレマイオスは、それまでのギリシャの天文学を集約し、さらに独自に発展させて『アルマゲスト』と呼ばれる著書に体系的にまとめあげた。本書で展開された天動説と円運動に基づく天体の運行の理論は逆行運動を含む惑星の運動をかなり正確に説明できたため、コペルニクスによる地動説が現れるまで1000年以上の長きにわたって人類の宇宙観を支配することになった。
プトレマイオス(Ptolemaeus)は、英語名がトレミー(Ptolemy)であり、受験数学の有名裏技「トレミーの定理」は彼の名を冠している。
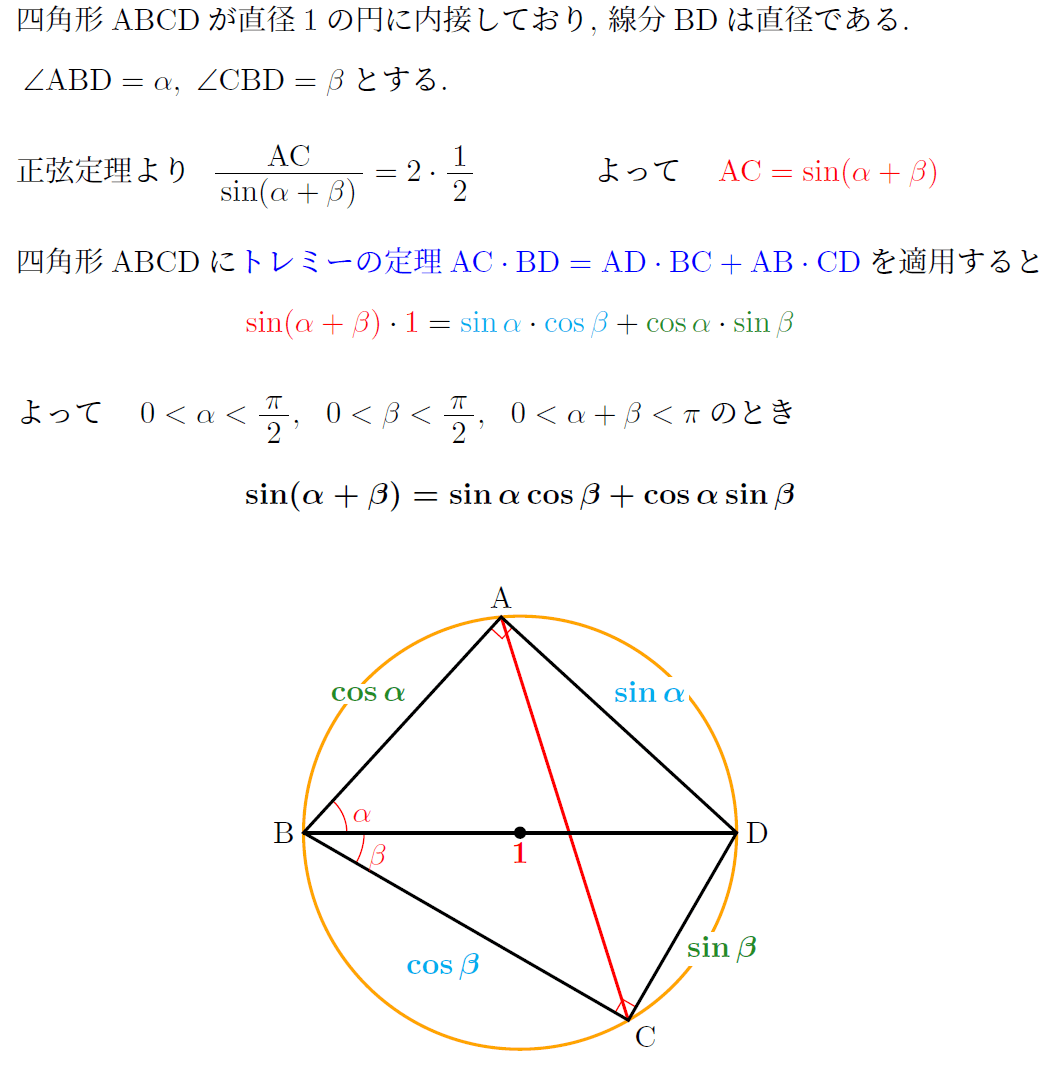
以下のように、トレミーの定理から三角関数の加法定理を容易に導くことができ、「アルマゲスト」には加法定理に相当するものが示されている。
![東京大学 数学入試問題72年 [1949~2020年入試全問題]](https://m.media-amazon.com/images/I/51W75gtrhiL._SL160_.jpg)


