
1998年東京大学後期第3問は、問題文からして只ならぬ様相を醸し出していた。
一見して高校数学とは思えないこの問題は、大学入試史上No.1の超難問として伝説を残した。
99%の大学受験生は問題を見た時点で心が折れることだろう。
鬼畜ともいえる難易度の参考として強烈なエピソードがあるので、次の書籍から引用する。
大学受験史上第1位にランクされる超難問である。難しいのは(2)で、実験をすると予想できるが完璧に論証するのは並大抵ではない。問題入手のとき、A予備校では解答作成を中断、帰宅することになったと聞かされた。最悪、翌日も解けないときはどうするかも話し合ったらしい。
翌朝B予備校関係者から電話があり、予備校の解答を出さなければならないから至急解いてくれという。そこでフランスに長期滞在中の友人C(大学助教授)とメールで連絡を取り、概要を説明し、解くことにした。何度かのやりとりの後、解答を作り上げたのは翌日のことである。
この正三角形の変換は大学の群論の最初に出てくる話だが、それを初等的な問題に応用したのは初めての経験である。
試験では完全解は無理でも十分性などの部分点はとれるだろう。その意味では良問といえるかもしれない。なお、A予備校の解答はCの知人のD教授が書いたものを参考にしたらしい。
さらに、Neural Fireworks から引用。
“誰もが入試史上最難問と認める問題がある.東大が本気を出していた97~98年にその問題は現れた.数学オリンピックに出題されても解ける人はいないだろうと言われたその問題は1998年東京大学後期数学第3問.長いので問題文は省略するが,ネットでもそこらじゅうに転がっているので,一度見てみるといい.
グラフ理論を題材にしたこの問題では答えはすぐに分かる.しかし論証は最強の難問で,完答者はゼロ.
私は当時勤めていた予備校にいた.私がいた予備校は後期日程に関しては解答速報を出さないため,私は個人的にせっせと解いていた.しかし,第3問で鉛筆が止まる.1時間以上考えたが論証が思いつかない.横で解いていた同僚も同じ.相当な難問だと思っていたが,さすがに大手予備校はもう解けているだろうと思い,河合塾で働く友人に電話する.しかし,河合塾はまだ解けていなかった.
大手予備校は東大の解答速報を当日にだす.しかし,どの予備校もなかなか解答速報が出ない.河合塾はその日の解答作成を断念,翌日にまわすことになったが,それでも解けなかったらどうしようと悩んだらしい.駿台も手も足も出ず,解答作成を急遽大数の安田先生に依頼した.
事態を把握してようやく,これは入試史上過去に例がないほどの超難問であると理解し,国際数学オリンピックメダリストの友人に電話する.ちょうど彼も別の予備校から依頼を受けて問題を解いている最中だった.その後,かなりの時間を要して友人は解答を出してくれた.
当時の東大は何がやりたかったのだろうかといまだに思う.97年・98年は前期後期ともDレベルの難問が続出(6題中Dレベルが3題,Cレベルが3題というセットもあった).たった2時間半では全完できた人は一人もいなかったであろう.良問もあったが,あれほど難しくしては差はほとんどつかない.
東大後期で数学がなくなった現在ではあのような難問が出題されることはあるまい.東工大AO入試も難問が多いとはいえ,本問に比べればはるかに簡単であろう.無理のない難問にレベルが抑えられ,適度に差がつくようになったが,たまに難問が大量に出題されていた当時を振り返り懐かしむことがある.”
解答
超難問と聞いて先入観を持った状態でいると、一瞬問題文を見ただけで題意の理解すら無理ゲーに思えてしまうが、あくまでも難しいのは(2)を厳密に論証する部分だけで、題意の理解は難しくはない。
やたらと冗長な問題文も、わかりやすく言い換えるとたったこれだけの話である。
1つの白頂点○から始め、[操作1]または[操作2]を繰り返す。
[操作1] 1つの頂点に新たな1つの白頂点を付加する。このとき、付加された方の頂点は白黒が反転する。
[操作2] 2つの頂点を結ぶ辺上に新たな1つの白頂点を挿入する。このとき、両側の2つの頂点は白黒が反転する。
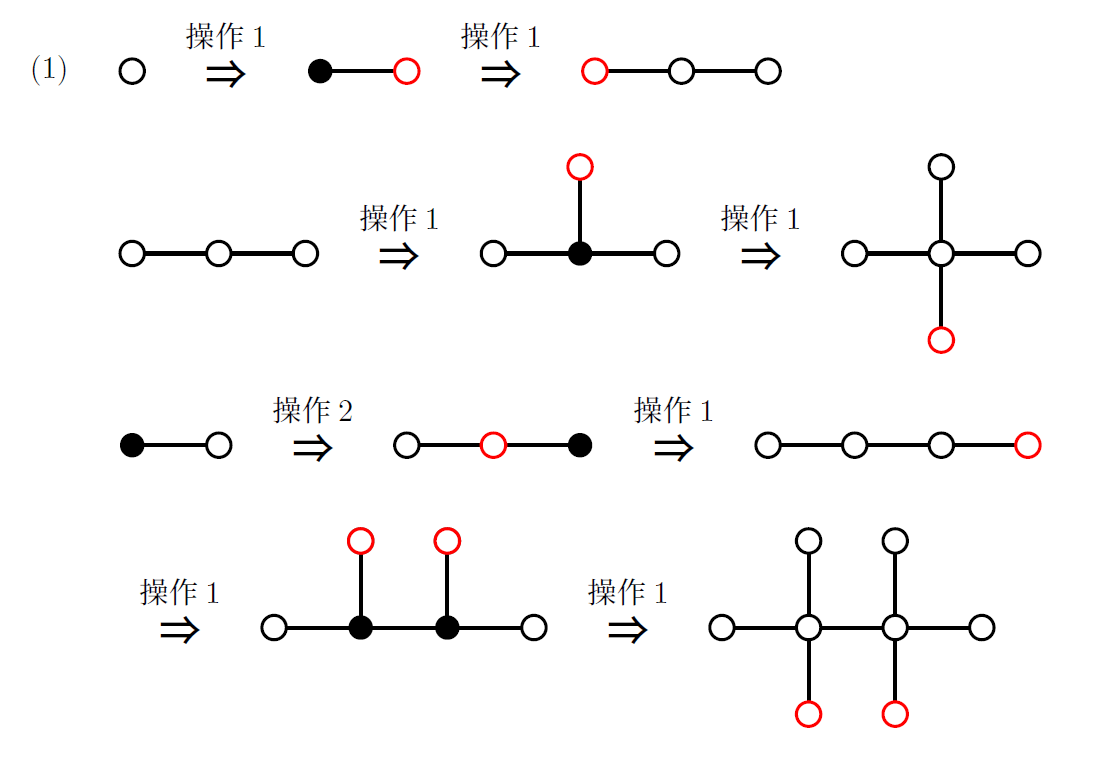
(1) 図5の3つのグラフの作成手順を示せ。
(2) 白頂点n個の一直線のグラフが作れるための必要十分条件は何か。
題意さえ理解できれば、(1)は小学生でも解ける。
新たに追加した白頂点を赤色で示している。手順は1通りではないが、1通り示せば十分である。
さて、問題の(2)であるが、まずは容易な予想までを示す。

ここまでは容易なので最低限である。
しかし、これの証明が伝説的難易度で、高校数学・受験数学で学習してきたような発想では困難なのである。
当時を知る関係者の方から直接メールを頂き、裏話を教えて頂いた。詳しいことは公開できないのだが、この方は当日の21時頃に問題をもらって帰宅し、翌日に『交代和をmodに関する不変量の観点から眺める』という解法の解答を提出したらしい。某予備校の先生も同日に同じ解法に到達していたとか。
一般に、あるモノを別のモノに変換することができないことを示したいとき、「不変量」が重要な戦略になりうるのだが、高校数学・受験数学においては学習しない上、普通は不変量が何かを見出すのも難しい。
証明の概略を示しておく。重要な発想が2つある。
- 両端に黒頂点を追加すると、[操作2]のみの考慮で済むようになる。
- 白頂点の個数の交代和を3で割った余りが不変量であることを示す。

グラフ理論
本問はいわゆるグラフ理論を背景にもつ問題であるが、ここでいうグラフは高校生が思い浮かべるような関数のグラフではなく、点や線の集合で構成された図形のことである。
グラフ理論は離散数学の一分野で、1736年に18世紀最大の数学者レオンハルト・オイラー(スイス)が示したケーニヒスベルクの七つの橋問題の解法にその萌芽を見ることができる。
オイラーは、東プロイセンの首都ケーニヒスベルク(現ロシア)の町の人が試みていた「この町の7つの橋を二度通らずにすべて渡って元の場所に戻れるか」という問題を右のようなグラフの問題に帰着させた。
彼は、現代的に言うと「一筆書きできるのは奇数本の辺が出る頂点が0個または2個のときに限る」ことを示し、この問題を否定的に解決した。なお、誤解されることが多いが、右のようなグラフはオイラーが論文の中で示したわけではない。グラフの一筆書きの問題はこの件とは独立に発展し、オイラーの証明と結びつけられたのは、オイラーの論文出版から150年以上も後の一般向けの数学パズルの本の中でのことであった。
絶対的な位置や長さや曲がり具合といった幾何学において重要であるはずの情報を削ぎ落とし、線のつながり方のみに焦点を当てて図形の本質的構造をとらえようとするオイラーの考え方は、当時としては画期的であった。
科学の様々な分野の問題や日常の多くの問題は、簡略化するとグラフで表すことができる。グラフ理論のグラフはネットワークとも呼ばれ、計算機科学、物理学、化学、生物学、社会科学などの学問はもちろん、組織図、家系図、路線図、旅行路、トーナメントの組合せ、さらにはゲームやパズルの解析といった娯楽用に至るまで幅広い応用をもつ。
オイラーは、このような図形のとらえ方を立体にも応用し、1750年に世界で二番目に美しい等式を見いだしている。
2022年から始まる新課程では、日本では初めてグラフ理論に関する内容が高校の教科書(数学C)に掲載される予定である。
問題の背景と出題のいきさつ
20年後の2018年、問題の背景と出題のいきさつが、2018年当時首都大学准教授であった小林正典氏によって大学への数学2018年1月号の中で明らかにされた。
以下の問題をグラフで表現すると、東大の問題に帰着するということである。
メビウスの帯を直線上にn個貼り合わせてできる図形を考える。すべての中心線で切り離したときに、1つの帯になるためのnの必要十分条件を求めよ。
この問題の詳細な説明は、日本数学会の数学通信第22巻第2号にて発表されており、ネットにはpdfで公開されている。
リアルな代数幾何―メビウスの帯からトロピカル曲線まで―.pdf(小林正典)
また、出題のいきさつは以下のようである。
小林正典氏が東京工業大学で助手をやっていた頃、シドニー大学で「特異点の爆発解析同値」の提唱者であるKuo先生とランチする機会を得た。そのときの話の中でこの問題が生まれ、Kuo先生と論文を共著することになった。
小林氏がその内容を東京大学で発表した少し後、この伝説となる問題が東大後期で出題された。小林氏が東大での出題を知ったのは、2003年に雑誌『数学セミナー』に新傾向問題のつもりで出題したときに、解答者から指摘されてのことであったという。
数学小説『予備校のいちばん長い日』
2022年、この伝説を題材としたフィクション小説が発売!
1998年・3月。東京大学理科一類の後期日程試験に、過去に類を見ない数学の奇問が出題された。
中堅予備校「七徳塾」の数学講師・言問さくらは、解答速報を出すべく早速この奇問に挑むも、まったく解けない。しかも信じられないことに、他の大手予備校も解答を作成できずにいるという。
さくらはこの問題が受験史に残る超難問であると確信し、大手予備校を出し抜き、どこよりも早く解答速報を出してみせると決意するのだが――。
立ちはだかるは、東大が出題した伝説の入試問題。いまだ語り継がれる実在した受験史上最悪の超難問に挑む、本格数学小説!
フィクションでも問題は本物なので解答(ここで示した解答とは異なる)作成までの過程を楽しめます♪
おまけ
ミレニアムサイエンススクールの早瀬ユウカちゃんすごいね~♪
JSユウカ#ブルアカ 100日チャレンジ Day 86 pic.twitter.com/6Y7RHo1Qx3
— Azel¦C103 1日目西ね05b (@lam) November 21, 2023





![大学への数学 2018年 01 月号 [雑誌]](https://m.media-amazon.com/images/I/51vsf74KWCL._SL160_.jpg)










