(2)の解答がI(p+1,q-1)となっていますが、B(p+1,q-1)の誤りですm(_ _)m
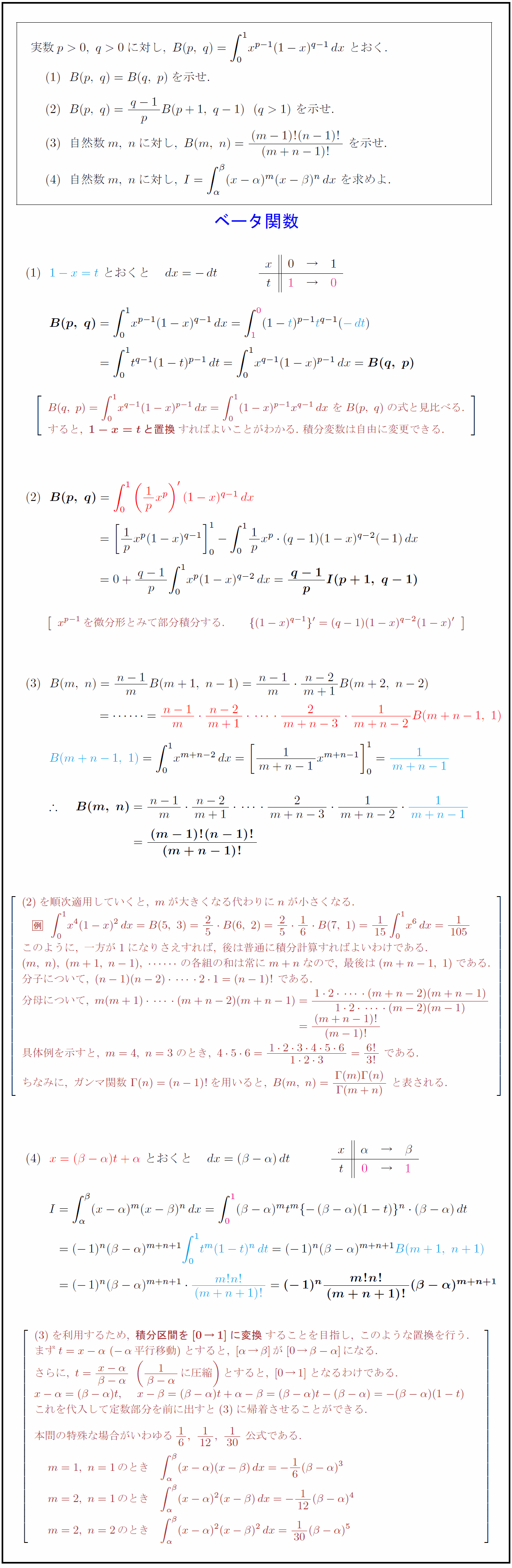
実数p>0,\ q>0に対し,\ B(p,\ q)=∫x^{p-1}(1-x)^{q-1}dx\ とおく.$ $B(p,\ q)=B(q,\ p)$を示せ. $B(p,\ q)={q-1}{p}B(p+1,\ q-1)(q>1)\ を示せ.$ $自然数m,\ nに対し,\ B(m,\ n)={(m-1)!(n-1)!}{(m+n-1)!}\ を示せ.$ $自然数m,\ nに対し,\ I=∫α}{β}(x-α)^m(x-β)^ndx\ を求めよ.$ B(q,\ p)=∫x^{q-1}(1-x)^{p-1}dx=∫(1-x)^{p-1}x^{q-1}dx\ をB(p,\ q)の式と見比べる. すると,\ {1-x=tと置換}すればよいことがわかる.\ 積分変数は自由に変更できる. x^{p-1}を微分形とみて部分積分する を順次適用していくと,\ mが大きくなる代わりにnが小さくなる. このように,\ 一方が1になりさえすれば,\ 後は普通に積分計算すればよいわけである. (m,\ n),\ (m+1,\ n-1),\ の各組の和は常にm+nなので,\ 最後は(m+n-1,\ 1)である. 分子について,\ 分母について,\ 具体例 ちなみに,\ ガンマ関数\ を利用するため,\ {積分区間を[0→1]に変換}することを目指し,\ このような置換を行う. まずt=x-α\ (-α平行移動)とすると,\ [α→β]が[0→β-α]になる. さらに,\ t={x-α}{β-α}\ ({1}{β-α}に圧縮)とすると,\ [0→1]となるわけである. これを代入して定数部分を前に出すとに帰着させることができる. 本問の特殊な場合がいわゆる16,\ {1}{12},\ {1}{30}\ 公式である.

