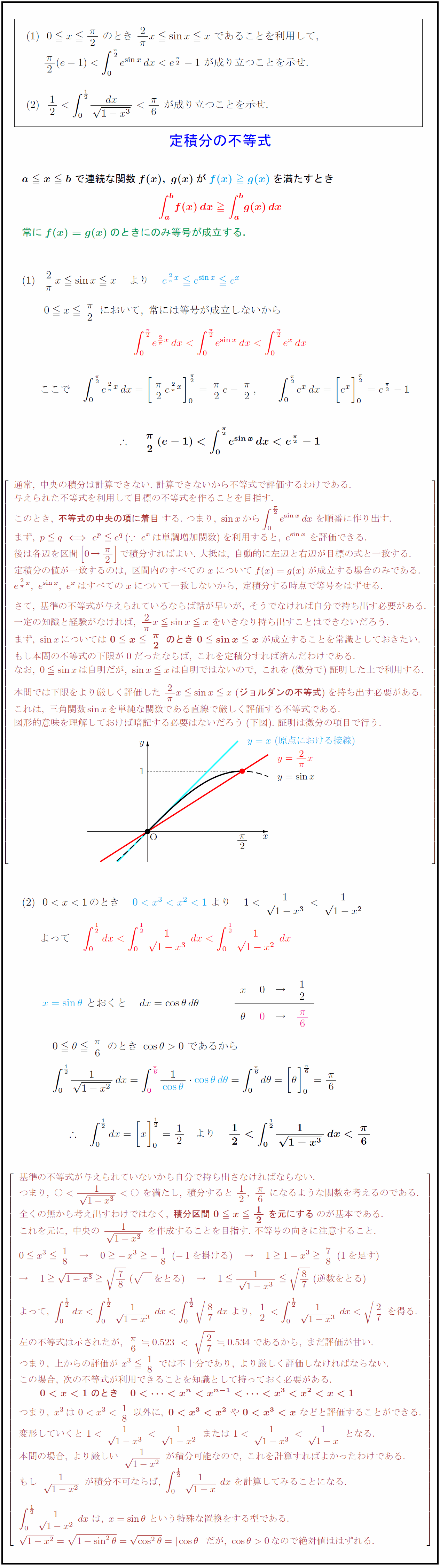
常には等号が成立しないから$ 通常,\ 中央の積分は計算できない.\ 計算できないから不等式で評価するわけである. 与えられた不等式を利用して目標の不等式を作ることを目指す. このとき,\ {不等式の中央の項に着目}する.\ つまり,\ sin xから∫0}{π/2e^{sin x}dx\ を順番に作り出す. まず,\ p qe^p e^q(∵\ e^xは単調増加関数)を利用すると,\ e^{sin x}\ を評価できる. 後は各辺を区間[0→{π}{2}]で積分すればよい.\ 大抵は,\ 自動的に左辺と右辺が目標の式と一致する. 定積分の値が一致するのは,\ 区間内のすべてのxについてf(x)=g(x)が成立する場合のみである. e^{2}{π}x},\ e^{sin x},\ e^xはすべてのxについて一致しないから,\ 定積分する時点で等号をはずせる. さて,\ 基準の不等式が与えられているならば話が早いが,\ そうでなければ自分で持ち出す必要がある. 一定の知識と経験がなければ,\ {2}{π}x sin x x\ をいきなり持ち出すことはできないだろう. まず,\ sin xについては\ {0 x{π}{2}\ のとき\ 0 sin x x}\ が成立することを常識としておきたい. もし本問の不等式の下限が0だったならば,\ これを定積分すれば済んだわけである. なお,\ 0sin xは自明だが,\ sin x xは自明ではないので,\ これを(微分で)証明した上で利用する. 本問では下限をより厳しく評価した\ {2}{π}x sin x x\ ({ジョルダンの不等式})を持ち出す必要がある. これは,\ 三角関数sin xを単純な関数である直線で厳しく評価する不等式である. 図形的意味を理解しておけば暗記する必要はないだろう(下図).\ 証明は微分の項目で行う. 基準の不等式が与えられていないから自分で持ち出さなければならない. つまり,\ ○<{1}1-x³<○\ を満たし,\ 積分すると\ 12,\ {π}{6}\ になるような関数を考えるのである. 全くの無から考え出すわけではなく,\ {積分区間\ 0 x12\ を元にする}のが基本である. これを元に,\ 中央の\ {1}1-x³\ を作成することを目指す.\ 不等号の向きに注意すること. 0 x³ 18 → 0 -x³-18\ (-1を掛ける) → 11-x³78\ (1を足す) → (逆数をとる) 左の不等式は示されたが,\ {π}{6}0.523\ <\ {27}0.534\ であるから,\ まだ評価が甘い. つまり,\ 上からの評価が\ x³18\ では不十分であり,\ より厳しく評価しなければならない. この場合,\ 次の不等式が利用できることを知識として持っておく必要がある.\ つまり,\ x³は\ 00なので絶対値ははずれる.

