
大阪大受験生 「各公式および頻出パターンは完璧に暗記し、難しい問題集も過去問もすべてやった。どんな問題が出ても大丈夫だ。」
だがしかし
大阪大教授 「基本公式の証明も当然できるよね?大丈夫だとは思うけど一応確認させてね。」

効率を重視しすぎて本質を見失っていた受験生
「し、しまったあああああああああ」
数学という学問に対して真摯に向き合ってきた受験生
「ラッキー♪サービス問題きたー」
問題用紙を開いて第1問を見た瞬間、多くの受験生は気付いた。
自身が数学という学問に対して真摯に向き合ってきていなかったことに。
すべては見透かされていたのだ。
「自分は今まで何をやっていたんだ・・・」「こんな問題すら解けないなんて・・・」等という思いが頭の中を駆け巡る。
第1問は後回しにして、とりあえず他の問題に手をつける。しかし、どうしても第1問が頭にちらついて離れない。「lim[x→0]sinx/xの証明証明証明証明・・・・・・」。今までに積み重ねてきた自身の受験勉強を根底から否定されて激しい動揺に見舞われた受験生は、半べそをかきながら残りの問題を解くことになる。
もちろん、合格は総合点で決まるのであるから、1問できなかっただけで完全に悲観的になる必要はない。しかし、これは普通の問題ではない。本来であればできて当然の問題である。さもなくば、今まで証明もできない公式を無闇矢鱈と使い回していたことになる。
本問ができなかった受験生は、仮に他の問題が解けたとしても、ある種の敗北感と共に試験会場を後にすることになったであろう。
普段当たり前のように使っている基本公式の証明が、毎年どこかの大学で出題されている。
しかし、難関大学で出題されるとそのインパクトは強烈なものとなる。
また、1999年の東大と同じく、理系と文系で同時に第1問での出題である。
この種の問題は往々にして受験生の出来が悪いという。第1問目でこの問題をみて「やられた」と唇をかんだ受験生も少なくなかっただろう。
これが出来ないほど悔しいことはない。1回は答えを見たことがあるはずなのだから。「ちゃんと教科書を読んでいれば・・・」と後悔しても後の祭りである。
「絶対に一度は見てるはずなんだ・・・思い出せ思い出せ・・・そうだ・・・教科書のあそこらへんだ・・・」などと念じてみるものの、証明が思い出されようはずはない。
それでも「何か書いておかなければ」と考えて、あることないことを適当に殴り書きをしている受験生の様子が想像される。
1999年の東大と異なるのは、理系と文系で違う問題ということである。文系のほうから解答を示す。
文系の「点と直線の距離公式の証明」は、結局は「公式を知らないものとして距離を求めよ」ということであり、その場で対応することが可能である。
様々な方法が考えられるが、点と直線の距離の公式を学習した図形と方程式分野の知識で求めるのが標準解答であろう。
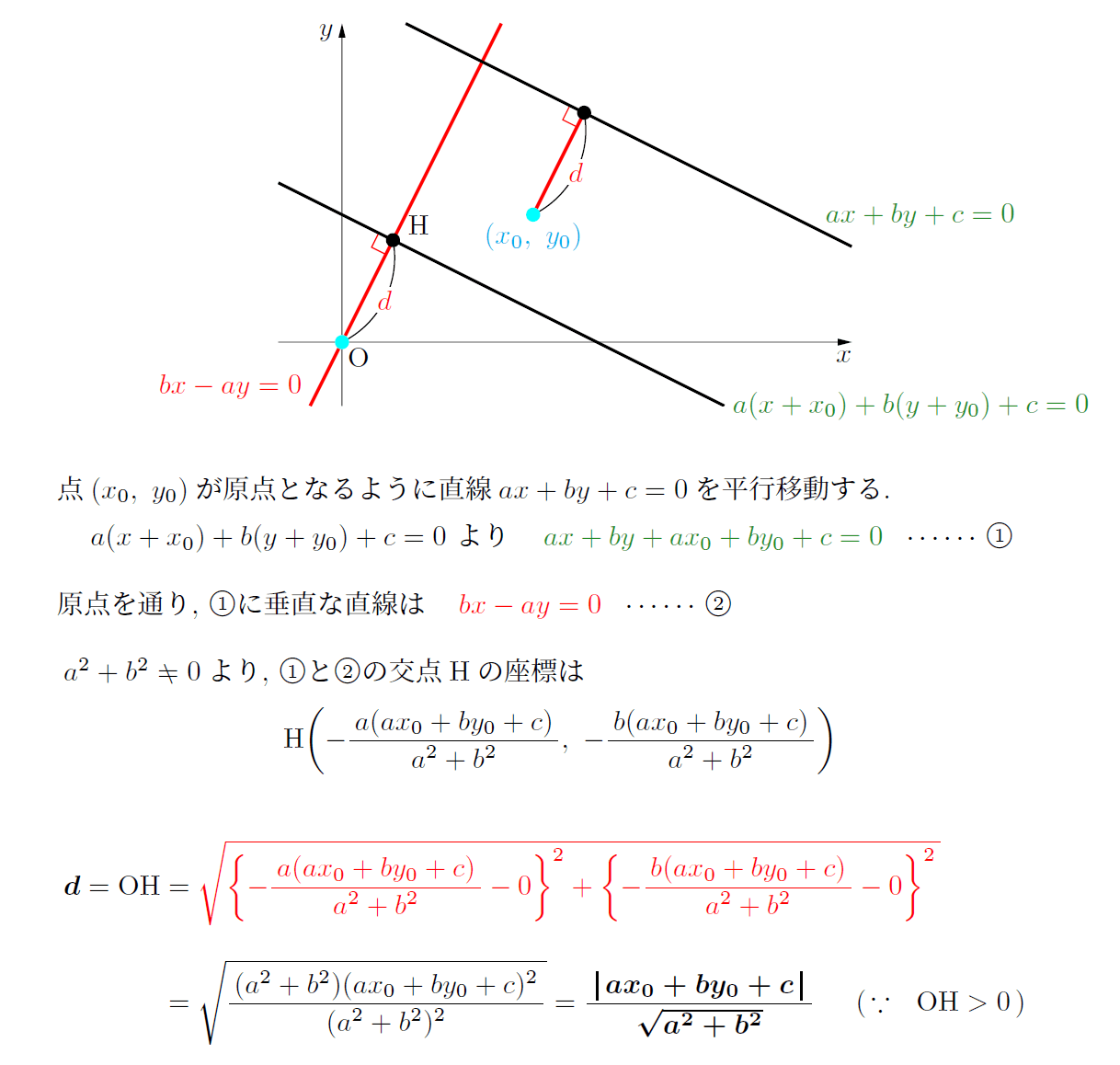
高校数学では、ベクトルを利用した証明も重要である。
同じ考え方で、空間の点と平面の距離の公式を導けるからである。

一方、理系の「sinx/xの極限」は証明方法を暗記していないとどうしようもあるまい。三角形と扇形の面積の大小比較からはさみうちの原理を用いるわけだが、考えて思いつくものではない。
ただし、導関数の定義を用いる (sinx)’=cosx の証明はできたはずである。

全理系大学受験生のうち、この lim(sinx/x)=1 の証明ができる受験生は果たして何割いるだろうか。
軽く過去問を調べた限りでは、5年に1回くらいはどこかの大学で出題されているので、受験生は要確認である。


