2010年 大阪大学　次元が違う！オイラーの世界で二番目に美しい数式からポアンカレ予想まで

2010年大阪大学理系第3問は、多少複雑だが、普通の不定方程式(整数解を求める整数問題)かと思われた。

しかし･･････

伝説の数学者「お主らに次元の違いを思い知らせてやろう･･････」　

受験生「そ、そんな･･････次元が違う･･････」

　

とりあえず、標準解答を示す。

整数分野を学習するようになった2015年以降の受験生にとっては標準レベルであるが、2010年当時の受験生にとっては難レベルである。

こうして、めでたく5つの組の解が求まる。はい、おしまい。

というのではあまりにもこの等式と問題作成者が不憫である。

おそらくはこの等式から発展した数学分野の研究者である問題作成者が特別な信条をもって出題したと自分には思えるからだ。

驚くべき等式の正体と発見の歴史、さらに等式の背景に果てしなく広がる数学を紹介しよう。

等式の正体

問題の等式の正体に気付くためのヒントはlの値に着目することである。

4　6　８　12　20

この5つの数字の組に心当たりがないだろうか。認知度はかなり高いはずである。

一方で、正体の等式の認知度はかなり低い。現代数学の源流であるにもかかわらず、高校数学・受験数学での存在感はないに等しく、そもそも2010年当時は高校範囲外であった。

しかし、ゆとり教育からの脱却が明確になった2012年から始まる新課程において学習することが決まっていたため、出題者がそれに先んじて出題しようと思ったのかもしれない。

　

lの5つの数字は、5種類存在する正多面体の面の数を表している。

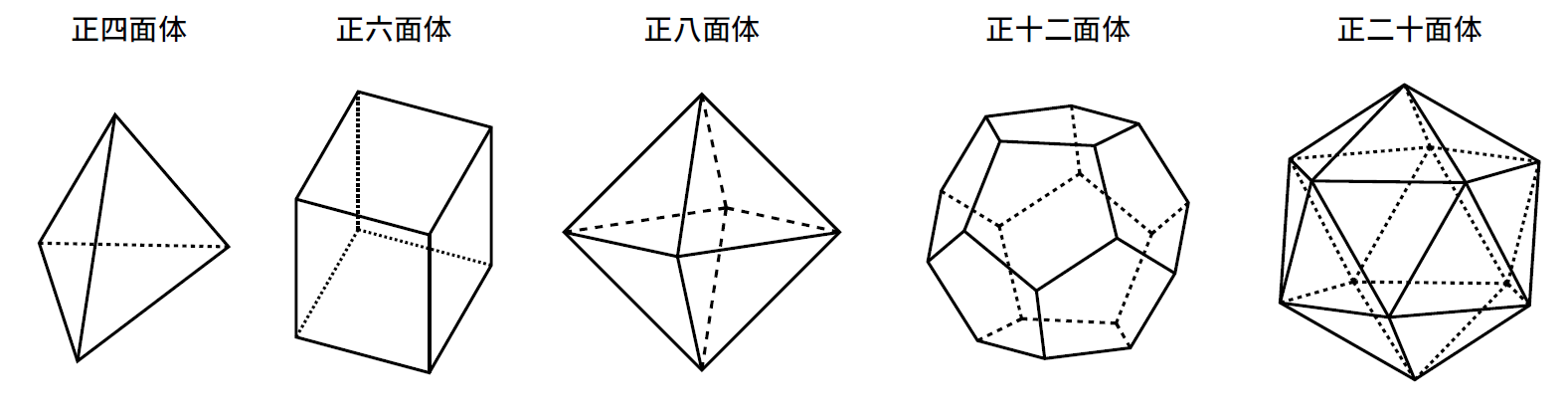
そして、この問題の不定方程式の解が5組であることは、正多面体が5種類しか存在し得ないことを示している。

なぜか。それは、この問題の等式の正体が次のオイラーの多面体公式に他ならないからである。

V－E＋F＝２

凸多面体の頂点(Vertex)、辺(Edge)、面(Face)の数の間に必ず成り立つ関係であり、2012年以降の高校生は数Aで学習している。とはいっても多くの高校では深入りせず、「一応こんな公式があります」程度で学習を終える。

5種類の正多面体について表にまとめると以下のようになる。正多面体の面が正p角形、頂点に集まる面の数をqとするとき、正多面体を{p,q}のように表すことがある(シュレーフリ記号)。これが問題のn,mの正体である。

	V(頂点)	E(辺)	F(面)	{n,m}	V－E＋F
正四面体	4	6	4	{3,3}	2
正六面体	8	12	6	{4,3}	2
正八面体	6	12	8	{3,4}	2
正十二面体	20	30	12	{5,3}	2
正二十面体	12	30	20	{3,5}	2

ここで、正多面体は以下の3条件を満たす多面体として定義される。

1. 凸多面体である
2. すべての面が合同な正n角形である
3. すべての頂点の周りの面の数mが等しい

もし条件3.がなかった場合、例えば正四面体を2つくっつけた立体(デルタ六面体)も正多面体に含まれてしまう。

以下のように、オイラーの多面体定理に正多面体であるための必要条件を組み込むと問題の等式が導かれる。

この方程式の整数解を求めることにより、正多面体が存在するとすれば多くとも5種類であることがわかるわけである。

　

オイラーの多面体公式は、世界で二番目に美しい数式とも評される。これは、アメリカの数学者に対して行われた美しい定理のアンケート結果に由来する。

1. e^iπ+1＝0（1748年オイラー）
2. オイラーの多面体公式　V－E＋F＝2（1750年）
3. 素数は無限にある（紀元前3世紀ユークリッド）
4. 正多面体は5種類ある（紀元前4世紀テアイテトス）
5. バーゼル問題（1735年オイラー）
6. ブラウワーの不動点定理（1910年）
7. √2は無理数である（紀元前5世紀ピタゴラス教団）
8. πは超越数である（1882年リンデマン）
9. 四色定理（1976年）
10. フェルマーの二平方定理（初証明は1749年オイラー)

一般人ではなく数学のプロに対して行われたアンケートにおいて、なぜオイラーの多面体公式が2位に選ばれたのだろうか。「シンプルで小学生でも理解できるから」といった単純な理由だけではあるまい。

おそらく、等式の価値を認識する数学者達は、深遠に潜む本質的な美しさに惹かれ、その等式から芽生えその後に育まれた豊かな数学の歴史に思いを馳せたからに違いない。

高校数学の片隅にひっそりとたたずんでいるだけのこの公式は、現代数学の礎となっている。

以下を読めば、数学者達がこの公式を選ばずにはいられなかった理由、選ばれるべくして選ばれたことがわかってもらえるかもしれない。

多面体理論の歴史

その完全な対称性と美しい調和性は、古代ギリシャの時代から数学者達を魅了してきた。

正四面体、立方体、正十二面体の発見はピタゴラス学派(紀元前5世紀)、正八面体と正二十面体の発見はテアイテトス(紀元前4世紀)とされることが多いが、それぞれの最初の発見が誰かについての統一見解はない。

一方で、初めて5つの正多面体を厳密で完全な形で研究したのがテアイテトスであることはまず間違いない。テアイテトスは5つの正多面体を幾何学的に構成し、共通する特徴を見抜き、さらに正多面体が5つに限られることを証明した。凸多面体の頂点に集まる平面角の総和が360°よりも小さくなることを用いる証明である。エウクレイデス(ユークリッド)の『原論』の第13巻のほとんどが正多面体に費やされているが、この内容はテアイテトスの業績に基づくものと考えられている。

プラトンはテアイテトスから正多面体について学び、著書「ティマイオス」で四元素論と正多面体を結びつけて記述したため、正多面体は「プラトン立体」とも呼ばれる。

万物が四大元素(空気、土、水、火)からなり相互作用するというプラトンの考えは、弟子のアリストテレスに受け継がれていく。この古代ギリシャの原子論は大きな影響力をもち、現代化学が誕生するまで広く受け入れられていた。

古代ギリシャで展開された多面体理論において最後に大きな貢献をした人物はアルキメデス(紀元前3世紀)である。アルキメデスは正多面体を拡張した半正多面体の概念を導入した。面に2種類以上の正多角形を用いてもよいというものであり、いわゆるサッカーボール型の切頂二十面体が有名である。アルキメデスが発見した13個の半正多面体は、今ではアルキメデスの立体と呼ばれている。

User Cyp on en.wikipedia, CC BY-SA 3.0, via Wikimedia Commons

アルキメデスの以後ギリシャ文明は衰退し、多面体の理論は長らく停滞した。人類が再び多面体に関心がもったのは、15世紀ルネサンスのヨーロッパにおいてであった。芸術家達は数学と芸術の両面から多面体を考察し、レオナルド・ダ・ビンチを始めとして多くの芸術家が多面体を作品に取り入れた。

16世紀、多面体に魅せられていた人物の中に数学者・物理学者のヨハネス・ケプラー(1571-1630)もいた。彼は多面体の理論や天文学に大きく貢献することになるが、驚くべきことに、そのきっかけとなったのは神秘主義的な思想であった。

神が数学的な美に基づいて世界を創造したと信じていたケプラーは、最初の著書『宇宙の神秘』(1596)の中で、当時発見されていた6つの惑星の軌道が5つの正多面体の入れ子構造と関係しているとする太陽中心の太陽系モデルを主張した。現代人から見ると馬鹿げた主張に思えるが、未だ人類の宇宙観がプトレマイオスの天動説に支配されていた時代に、コペルニクスの地動説の支持を出版して公言した最初の天文学者となった。

Johannes Kepler, Public domain, via Wikimedia Commons

ケプラーが歴史に名を刻むのは、これを単なる空想で終わらせず、天文学的なデータに基づく理論的な裏付けを試みたからである。ケプラーは、観測データと自分の理論の食い違いを克服するために、様々な説明や工夫を試みた。そのことが結果として、彼を真実に近づけることになる。

最終的に、ケプラーは自身の太陽系モデルが間違っていることを証明しただけでなく、科学史における偉大な功績の1つとなる惑星運動の3法則を発見した(高校物理で学習)。これらは、ケプラーの死後30年後にアイザック・ニュートンによって数学的に証明された。

ケプラーは、晩年には多面体理論についても大きな貢献を残した。『宇宙の調和』(1619年)では、13個のアルキメデスの立体を再発見し、かつ半正多面体が13個に限られることを証明した。また、4個存在する星形正多面体(正多面体の各辺や各面を交わるまで延長したときにできる多面体)のうち2個(下図)を発見した。これらはケプラーの多面体と呼ばれる。

User Cyp, CC BY-SA 3.0, via Wikimedia Commons

『宇宙の調和』には、受験数学でも役立つ正多面体の双対性への言及もある。

	V(頂点)	E(辺)	F(面)
正四面体	4	6	4
正六面体	8	12	6
正八面体	6	12	8
正十二面体	20	30	12
正二十面体	12	30	20

正六面体と正八面体、正十二面体と正二十面体はそれぞれ頂点と面の数を入れ替えた関係にあり、これを双対性という。正四面体は頂点と面の数が等しく自分自身と双対関係にあるので自己双対である。ケプラーは、互いに内接させることができるという双対性の図形的解釈に気付いた。

このケプラーの貢献からさらに1世紀以上経過した18世紀、ついに数学史上に燦然と輝く伝説の数学者が登場し、多面体の理論に最大級の貢献をすることになる。

伝説の数学者　レオンハルト・オイラー（スイス；1707-1783）

Jakob Emanuel Handmann, Public domain, via Wikimedia Commons

レオンハルト・オイラーは、歴史上最も偉大な数学者の1人であり、18世紀最大の数学者である。

ニュートンが数学を自然界に応用し多くの科学的な実績を残していた18世紀初頭、オイラーはスイスのバーゼルで誕生した。

1720年、わずか13歳にしてバーゼル大学に入学して哲学を学んだが、スイスで有名な数学者一族ベルヌーイ家のヨハン・ベルヌーイに数学の才能を見い出された。1735年にバーゼル問題を解決したことで一目置かれる存在になる。

オイラーは、人間離れした計算力と記憶力で膨大な計算を暗算で行うことができた。8桁同士の掛け算を数秒、寝付けなかったときには100までの整数の6乗を暗算していたなど、伝説的エピソードに事欠かない。

数学のあらゆる分野に基礎から応用まで、さらには物理学にも膨大な業績を残した。オイラーの公式、オイラー定数、オイラー方程式、オイラー関数、オイラー予想、オイラー近似、一筆書きができる必要十分条件(オイラーグラフ)、オイラー線、オイラーの多面体公式、オイラーの運動方程式など、様々な分野で頻繁にオイラーの名が登場する。他の数学者の名を冠していても実はオイラーの貢献による業績も多い。また、π、sin、cos、i、e、Σ、y=f(x)、三角形の角Aの対辺のaなど現在世界中で使用されている記号を普及させた。さらには、幾何学で表現されていたニュートン力学を「ma=F」という現在の解析的表現に変更したのもオイラーである。当時まだ市民権を得られていなかった虚数iを積極的に活用してその有用性を広めた功績も大きい。数学者には珍しく、学生に研究成果を平易に解説することにも長けており、教育者としても優秀であった。

非常に温厚で性格で、膝の上で子守をしながら論文を執筆していたとされる。国家に対しても従順で、暦の作成、硬貨の鋳造、運河の設置、水道の設計、大砲の改良、航海表の作成など様々な問題を解決した。

悪環境やストレスから、30歳になる頃には片目を、60歳になる頃には両目を失明してしまうが、論文を書くペースは全盲になっても全く変わることはなく、1783年に76歳で亡くなるその日まで数学に没頭していたという。

オイラーは1年間に普通の数学者の一生分に相当する平均800ページもの論文を書いたため、人類史上最も多くの論文を書いた数学者である。オイラーの論文は5万ページを超える全集にまとめられて1911年から刊行され続けているが、その全集は100年以上たった今日でも完結していない。

参考文献　レオンハルト・オイラー - Wikipedia

「辺」の発見から多面体公式へ

既に述べたように、5つの正多面体は2000年前には知られていた。

しかし、正多面体に魅せられていたピタゴラス、プラトン、ユークリッド、アルキメデス、ケプラーといった歴代の名だたる大数学者達はこの小学生レベルの等式を見逃してしまっていた。

V－E＋F＝2

1750年、オイラーはゴールドバッハへの手紙の中でこの公式を示した。下表に隠れた等式が2000年の長きを経てようやく発見されたわけである。

	V(頂点)	E(辺)	F(面)
正四面体	4	6	4
正六面体	8	12	6
正八面体	6	12	8
正十二面体	20	30	12
正二十面体	12	30	20

それにしても、この表を見て2000年間誰も等式に気付かなかったなどということがありえるのだろうか。どう考えてもおかしい。であるならば、そもそもこの表自体が存在しなかったと考えるのが自然である。

ではなぜこの表が存在しなかったのか。

その答えも、ゴールドバッハへの手紙に記されたオイラーの言葉から窺い知ることができる。

「2つの面がその周囲で接する接合部分を表す用語がないので、私はそれを「辺」と呼ぶ」

そう、オイラーの登場まで人類の意識の中に多面体の「辺」は存在しなかったのだ。

それまでの数学者にとって、多面体に対する興味は長さ・角度・面積・体積などの幾何学的な計量であり、その構造について理解しようとはしなかった。

一方、オイラーはその本質を問うた。

そもそも多面体とは何か

そして、天才的な洞察力によってその真髄に到達してみせた。

「3次元多面体は頂点(0次元)と辺(1次元)と面(2次元)で構成されている！」

いったん3つの構成要素を把握して様々な多面体でその数を数え始めたならば、V－E＋F＝2の発見は自然な流れであろう。

多面体公式の発見は、次元の違う構成要素に焦点を当てて多面体の本質をあぶり出した文字通りの異次元的な成果であったのだ。

オイラーは、1750年と1751年に2つの論文の中で多面体公式の証明を示したが、現代的な基準で厳密なものではなかった。また、オイラーがこの後多面体公式について書くことはなかった。

多面体公式は後の数学者達によって厳密に証明され、無限の広がりを見せていく。オイラーは知る由もなかったが、多面体公式は予想を超えて遙かに図形の本質に迫りうる等式であった。

多面体公式の適用限界

オイラーは凸多面体と仮定して多面体公式を示したが、その後の100年間で多面体公式はより一般的な多面体にも適用できることがわかってきた。

一方で、以下のような多面体公式を満たさない複雑な多面体も続々と発見された。凸多面体は多面体公式が成り立つための十分条件であるが、必要条件ではなかった。

どんな条件の多面体ならば多面体公式を満たすのか、数学者達は必要条件を探っていった。

その中でもドイツのシュタウトは特に優れた仕事をした。彼の証明は広い範囲の凸でない多面体にも適用でき、また、多面体公式を満たす多面体の非常に一般的な基準を与えた。

• どの頂点からどの頂点へも辺の道を辿っていける。
• 同じ頂点で始まり、終わる辺の道は多面体を2つに分ける。

シュタウトのこの基準は、わかりやすい表現に言い換えると、多面体がゴムで作られていたとして、空気を入れて膨らませて丸い風船のようにできる多面体のことである。もしトンネルが1つある場合、膨らませても丸くはならずドーナツ型となるから多面体公式を満たさない。

多面体公式を満たすか否かの境界を探る19世紀前半の豊かな議論は、19世紀末の位相幾何学(トポロジー)誕生の舞台を用意した。

位相幾何学(トポロジー)爆誕！

19世紀中頃になると、多面体公式の曲面への一般化が試みられるようになる。

例えば、地球表面(球面)ならば緯線と経線を引いてその交点を頂点にもつような多面体と見なせる。辺や面は曲がっていてもその数は直線的な場合と変わらないから、普通の凸多面体と同様に多面体公式が成り立つ。

こうして、幾何学は位相幾何学(トポロジー)へと変化していく。オイラーにその研究の萌芽をみたトポロジーは、20世紀初頭よりフランスの数学者アンリ・ポアンカレ(下)によって体系化され、数学の一大分野としての地位を確立する。19世紀の純粋数学の3本柱は代数学・解析学・幾何学であったが、20世紀には代数学・解析学・トポロジーになった。実際、1936年に創設された数学のノーベル賞とも称されるフィールズ賞受賞者の1/3がトポロジーの研究で受賞している。

Public domain, via Wikimedia Commons

トポロジーは、オイラー以上に図形の本質に迫る。

そもそも形とは何か

トポロジーは「ゴム膜の幾何学」や「柔らかい幾何学」とも称され、剛体的な図形の長さや面積などを考察した従来の幾何学とは対称的に、切り貼りせずに「連続的」な変化によって重なる図形は同じものとみなしてその性質を考察する。

すると、図形に本来的に備わっている性質(位相)の違いがV－E＋Fの値(オイラー標数χ)の違いとなって現れる。

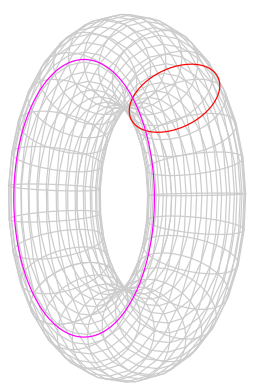
球面やすべての凸多面体などはいずれもV－E＋F＝２を満たすから、トポロジー的に同じ形である。一方、穴が１個ある立体はV－E＋F＝０となり、穴１個のトーラス(ドーナツ)とトポロジー的に同じ形となる。トーラスは球面とは本質的に別の形であり、実際ドーナツ状のゴム膜はどう連続的に変化させたとしても、切り貼りしない限り球面状にすることはできない。

曲面によってV－E＋Fの値(オイラー標数χ)が異なるから、これを基準として形を分類することができる。オイラー標数χに加えて表裏の有無と境界数を考慮すると、曲面は完全に決定する。

曲面	χ	表裏	境界数
球面	2	あり	0
穴1個のトーラス	0	あり	0
穴2個のトーラス	－2	あり	0
穴g個のトーラス	2－2g	あり	0
円板	1	あり	1
円柱	0	あり	2
メビウスの帯	0	なし	1

トポロジーは、現在では物理学(宇宙の構造や超ひも理論など)、化学(化合物の構造など)、分子生物学(DNAの構造など)、情報科学(ネットワークの構造など)、建築学、心理学、疫学、経済学、3DCGに至るまで多様な応用がなされている。

ポアンカレ予想

上の表で分類した曲面はトポロジー的にはすべて2次元図形である。図形が置かれてるのは3次元空間であるが、仮にその表面上に人がいるとしたら、その移動の自由度は2だからである。

アンリ・ポアンカレは、n次元における同様の分類を夢見たが、3次元における分類ですら叶わなかった。しかし、3次元について考察する中でのポアンカレの問いかけは、20世紀の最も有名な未解決問題の1つとなった(1904年)。

「単連結な3次元閉多様体は3次元球面と位相同型か？」

2000年にアメリカのクレイ数学研究所が100万ドルの懸賞金を賭けた問題の1つであることでも有名である(ミレニアム懸賞問題)。

　

ポアンカレ予想は、我々が住む3次元宇宙の形の予想と解釈することもできる。トポロジーならば、従来の幾何学では到底手の届かないところにあった宇宙の形までもが考察対象になる。

さて、3次元宇宙を外から眺めることができればその形は直ちにわかるが、3次元宇宙の中に生きる我々は内在的な情報によってその形を推測するしかない。

このことは2次元で考えるとわかりやすい。2次元の地球表面上にいながらにしてその形が球面であることを確認するにはどうしたらよいかということである。

当然、単に1周回ってみただけで地球が丸いことの証明にはならない。例えば、トーラス形であっても1周が可能である。

ポアンカレは、ロープを使った方法を考えた。ロープの一端を固定し、他方を持って地球を一周してループを作る。このロープを地球表面に沿ってすべて回収することができたならば地球は丸いといえるのではないか。

Salix alba at English Wikipedia, CC BY-SA 3.0, via Wikimedia Commons

もし地球がトーラス形であった場合、どう1周したとしても穴にひっかかるので地球表面に沿ってロープを回収することはできない。

Krishnavedala, CC0, via Wikimedia Commons

「以上の2次元の話が3次元宇宙でも成り立つか」という問いかけがポアンカレ予想である。

　

ポアンカレ予想の証明は困難を極めた。最も大きな障害は、ロープを回収しようとしたときにいわば絡まって結び目が生じてしまうことであった。何とかして結び目をほどこうとした数学者達の試みはすべて失敗に終わった。

トポロジーが数学の王者としての地位を築きつつあった1960年、スティーブン・スメイル(アメリカ)は宇宙がより高次元空間であったとしたらどうなるかを考え、5次元以上で成り立つことを証明した(1966年フィールズ賞)。驚くべきことに、高次元のほうが証明が簡単なのである。これは、高次元ではロープの絡み合いがなくなることに起因する。たとえるならば、道路と線路を2次元で交差させると踏切で渋滞が発生するが、3次元の立体交差にするとスムーズに交通が流れるようなことである。

1982年になってようやくマイケル・フリードマン(アメリカ)が4次元の場合を証明した(1986年フィールズ賞)。ポアンカレ予想の3次元にあと一歩まで迫ったかに思われたが、高次元から攻める試みがその後進展することはなかった。

ウィリアム・サーストン(アメリカ)は、全く新しいアプローチが必要だと考えた。ポアンカレ予想は「ロープを回収できれば宇宙は丸い」という予想だが、宇宙が丸くなかった場合については何も言及していない。サーストンは、宇宙がとり得る形をすべて調べ挙げられないかと考えた。10年以上にわたる試行錯誤の末、1982年に「宇宙がどんな形であろうとも、最大で8種類の異なる断片から成り立っているだろう」という幾何化予想を提唱した。

この幾何化予想はポアンカレ予想を包含する壮大な予想である。8種類のうち1つは丸い形、それ以外は丸くない形であり、丸くない形が1つでも含まれているとロープが回収できないからである。つまり、サーストンの幾何化予想が正しければ、「ロープが回収できれば宇宙は丸い」とするポアンカレ予想も正しいといえるわけである。

幾何化予想の証明に多くの数学者が取り組み始めた1990年代、アメリカに1人のロシア人数学者が降り立った。

George Bergman, GFDL 1.2, via Wikimedia Commons

後に幾何化予想を証明することになるグリゴリー・ペレリマン(1966-)である。数学教師の母親に英才教育を受けたペレリマンは、当時最年少の16歳で国際数学オリンピックに出場し、満点を獲得するほど数学に長けていた。同時に物理学でも卓越した才能を発揮していたという。

ペレリマンの研究分野は、トポロジーに王座を明け渡したと言われた微分幾何学であった。アメリカにいる間にソウル予想を解決するなど微分幾何学の発展に大きく貢献して数学者の間ではよく知られた存在になったペレリマンであったが、突然人付き合いを断つようになる。1995年、ペレリマンは「難問を解決できる可能性がある」と言い残してロシアに戻った。

それから7年後の2002年、インターネット上に突如幾何化予想とポアンカレ予想の証明を投稿して数学界を驚かせた。当初多くの数学者は疑っていたが、証明に間違いは見当たらない。

2003年、トポロジーの専門家で埋め尽くされたアメリカの会場でペレリマンによる解説が行われた。

ペレリマンの証明は衝撃的なものであった。ペレリマンは、トポロジーではなく自分の専門分野である微分幾何学に加え、物理学の知識を駆使し、いわば宇宙を温めて変形しながら8つの断片に分解してみせた。解説にはエネルギー、エントロピー、温度など数学では決して使われない物理学の用語が次々と登場した。トポロジーの専門家達は、証明が終わってしまったことに落胆し、トポロジーが使われなかったことに落胆し、証明が理解できないことに落胆した。

最終的に、ペレリマンが2002年から2003年にかけて執筆した3つの論文は数学者達の4年の検証を経て正しいことが確認された。

ペレリマンには2006年にフィールズ賞、2010年にクレイ研究所のミレニアム賞が授与されることになったが、彼はいずれの受賞も辞退し、賞金やメダルの受け取りも拒否したことでも数学界に衝撃を与えた。

超天才の彼には証明がすべてであり、名誉や賞金は重要ではなかったのだ。

ペレリマンについてはその特異な人物像に焦点が当てられることも多いが、彼が数学で果たした偉大な功績を忘れてはならない。

参考文献