2003年 日本女子大学　素数の謎を解き明かせ～オイラー・ガウス・リーマンの挑戦～

2003年日本女子大学理学部の自己推薦入試において、非常に有名な等式を導く問題が出題された。

問題を見てわかる通り、最後の等式までの道のりは非常に長い。

(1)～(3)は頻出パターン問題であるが、(4)以降はかなり難しい。解答を示しておく。

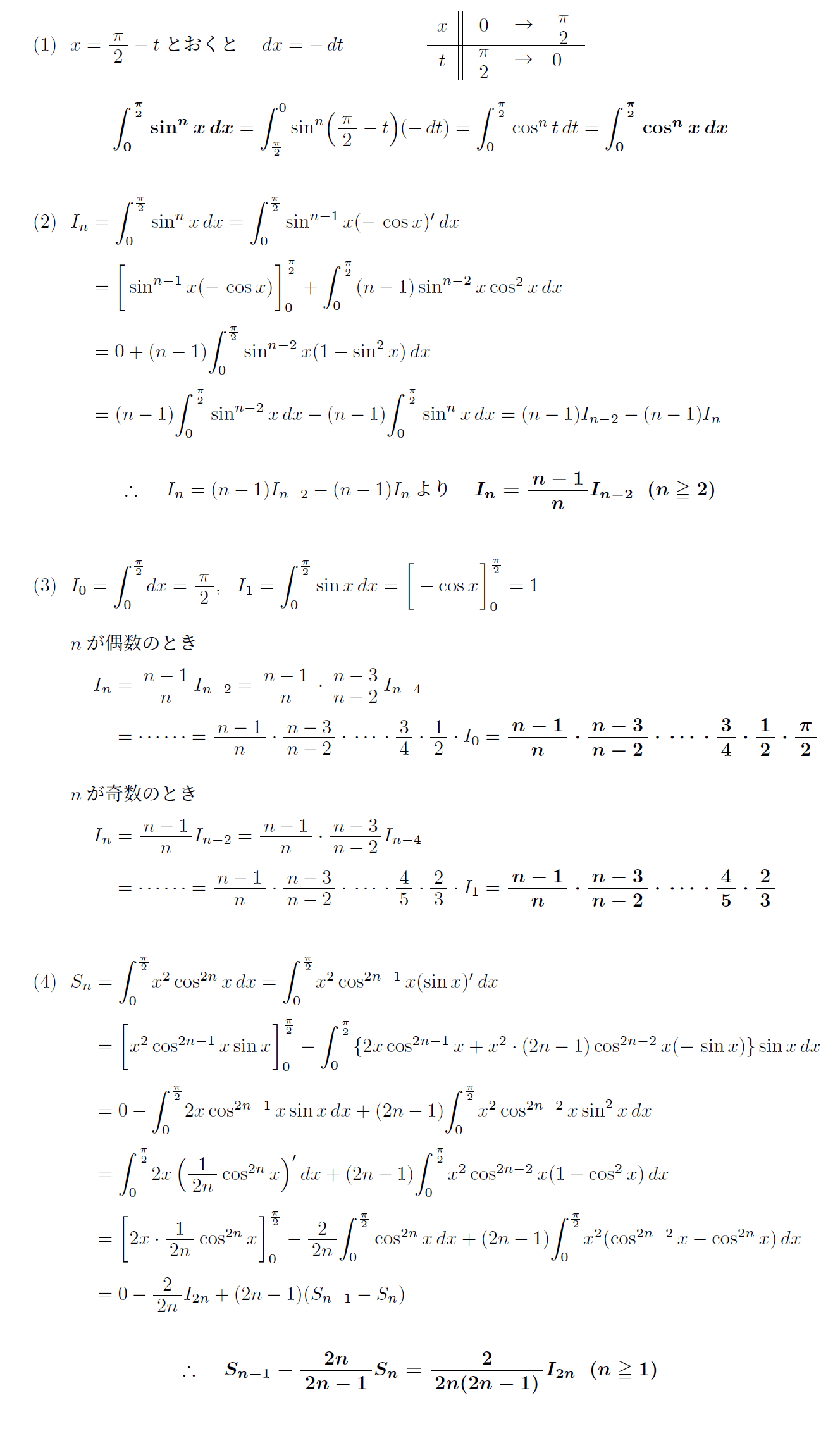
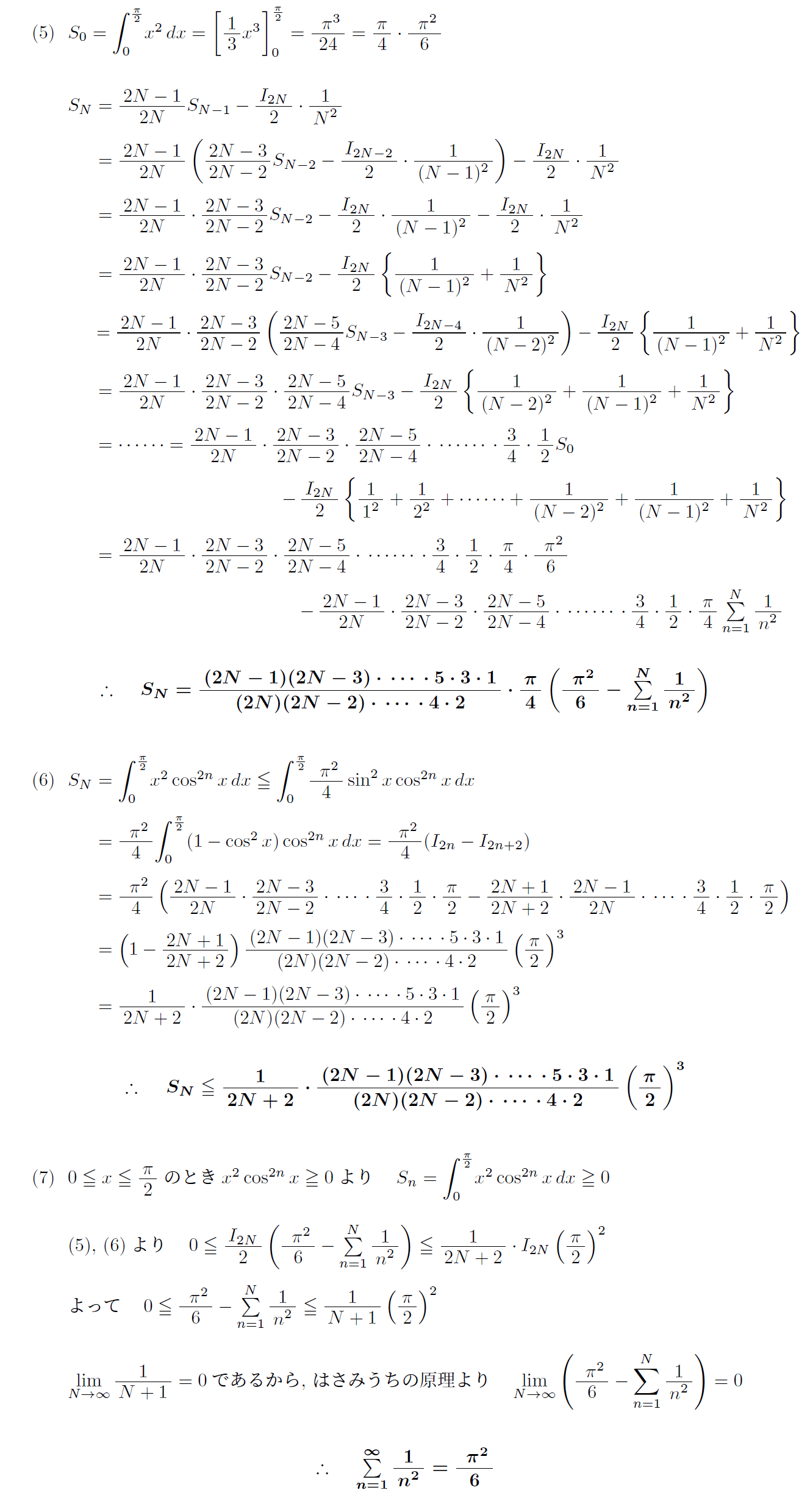
さて、最終的に得られる平方数の逆数の無限和は、数学上計り知れない価値がある。

この無限和を不等式で評価する問題は割とよく出題されるが、値をズバリ求める問題は難しく、一般入試では出題されることはまずない。自己推薦入試ならではの出題である。

以下で、素数に魅せられた数学者達の足跡を辿りながら等式の背景に広がる数学の世界を堪能してもらいたい。

最初に伝説となっている2人の数学界の巨人を紹介する。 

18世紀最大の盲目の数学者レオンハルト・オイラー（スイス ; 1707-1783）

Jakob Emanuel Handmann, Public domain, via Wikimedia Commons

レオンハルトオイラーは、歴史上最も偉大な数学者の1人であり、18世紀最大の数学者である。

ニュートンが数学を自然界に応用し多くの科学的な実績を残していた18世紀初頭、オイラーはスイスのバーゼルで誕生した。

1720年、わずか13歳にしてバーゼル大学に入学して哲学を学んだが、ヨハン・ベルヌーイに数学の才能を見い出された。1735年にバーゼル問題を解決したことで一目置かれる存在になる。

人間離れした計算力と記憶力で膨大な計算を暗算で行うことができたオイラーは、数学のあらゆる分野に基礎から応用まで、さらには物理学にも膨大な業績を残した。オイラーの公式、オイラー定数、オイラー方程式、オイラー関数、オイラー予想、、オイラー近似、一筆書きができる必要十分条件(オイラーグラフ)、オイラー線、オイラーの多面体定理、オイラーの運動方程式など、様々な分野で頻繁にオイラーの名が登場する。また、π、sin、cos、i、e、Σ、y=f(x)など現在世界中で使用されている記号を普及させた。さらには、幾何学で表現されていたニュートン力学を「ma=F」という現在の解析的表現に変更したのもオイラーである。当時まだ市民権を得られていなかった虚数iを積極的に活用してその有用性を広めた功績も大きい。

オイラーは1年間に普通の数学者の一生分に相当する平均800ページもの論文を書いたため、人類史上最も多くの論文を書いた数学者であった。

悪環境やストレスから、30歳になる頃には片目を、60歳になる頃には両目を失明してしまうが、論文を書くペースは全盲になっても全く変わることはなく76歳で亡くなるその日まで数学に没頭していたという。

オイラーの論文は5万ページを超える全集にまとめられて1911年から刊行され続けているが、その全集は100年以上たった今日でも完結していない。

参考文献　レオンハルト・オイラー – Wikipedia

19世紀最大の数学者カール・フリードリヒ・ガウス（ドイツ ; 1777-1855）

Gottlieb Biermann, Public domain, via Wikimedia Commons

カール・フリードリヒ・ガウスは、1777年ドイツのブラウンシュヴァイクで生を受けた。

オイラーと並び称され「数学王」との異名を取る人類最高の数学者の一人であり、近代数学のあらゆる分野で先駆的な役割を果たした。

言葉を話せるようになる前から計算ができ、3歳のときに父親がしていた職人達に支払う給料の計算の誤りを指摘したという。また、7歳のときには1から100までの和5050を現在でいう等差数列の和の公式を用いて瞬時に求め、教師を驚かせた。15歳のときには素数定理を予想、18歳のときには最小2乗法の発見、19歳のときには合同式を用いた合同算術を発明し、平方剰余の相互法則を証明した。また、同時期に正17角形が定規とコンパスだけで作図可能なことも証明した。作図可能な正素数角形の発見は、正三角形と正五角形以来約2000年ぶりのことであった。学位論文では、代数学の基本定理「n次方程式は複素数の範囲でn個の解をもつ」に完全な証明を与えた。

正17角形が作図可能であることに興奮したガウスは、数学者になることを決意し、そのときから数学日誌をつけ始めた。ガウスは性格上多くの結果を得ながらも公表しなかったが、この日誌のおかげでガウスの業績を確認できる。

ガウスの業績は、代数学、数論、複素平面、関数論、非ユークリッド幾何学など広範囲に及び、電磁気学、天文学など物理学の発展にも大きく貢献した。そのことは、ガウス記号、ガウス曲率、ガウス関数、ガウス整数、ガウスの法則、ガウス平面、ガウス積分など、ガウスの名にちなんだものが多岐にわたることからも分かる。

特に数論への貢献が大きく、1801年に発表された「ガウス整数論」をもって今日の「数論」という分野が誕生したとされている。発表はしなかったものの、解析学でも時代を数十年を先んじた研究を行っていた。まだ複素数が市民権を得ていなかったが、20歳の頃には今日用いられている形式で複素平面(ガウス平面)を論じていた。その結果、アーベルによって世に発表される30年前にすでに楕円関数を発見していたという。

1801年、天文学者達はケレスと呼ばれる小さな新惑星の発見に沸いていたが、太陽の向こう側の軌道に入ってから見つけることができなくなってしまった。このころの天文学者はただ望遠鏡を向けるだけで、軌道を予測する数学的手法をもっていなかったのである。

そこに、24歳のガウスが登場して数学的に軌道を予測した結果、ケレスは難なく見つかった。数学者には既に知られた存在であったガウスはこの発見によって科学界の寵児となった。

また、この偉業は科学が急速に発展し始めた時代において数学が持つ予測能力を象徴したものとなった。この功績によりガウスはゲッティンゲン天文台長に就任し、終生そこに勤めた。

以降、物理学とりわけ電磁気学における重要な発見をいくつも成し遂げ、1855年に77歳の生涯を閉じた。

素数の配列の謎

試しに、10000から10100までの素数を書き出すと次のようになる。

10007　10009　10037　10039　10061　10067　10069　10079　10091　10093　10099

差が2ですぐに素数が出てきたと思えば、20以上素数が出てこないなど素数の並びには全く規則性が感じられない。

オイラーは「素数の並びには必ず意味があり、自然や宇宙と関係があるはずだ」という強い信念を持ち、素数の規則性を探すために次々に素数をあぶりだしていった。しかし、5万を超えても一向に規則性が表れる気配はない。そんなオイラーに対し周囲は冷ややかだった。

多くの数学者は、素数は何の意味も持たない単に無秩序な数だと考えていたのである。しかし、オイラーはそんな批判を一気にはねのける発見をすることになる。

オイラーが解決したバーゼル問題と素数の結びつき

バーゼル問題とは、「平方数の逆数の無限和を求めよ」という問題であり、1644年に提起された。

スイスのバーゼル在住のベルヌーイが挑んだものの解決できず、そのまま後世に託した問題であるためバーゼル問題と呼ばれるようになった。2003年日本女子大学の入試問題はまさにバーゼル問題に対する解答を与えたものである。

バーゼル問題は、1735年にオイラーによって解決された。ただし、その方法はこの入試問題の誘導とは異なる。わずかに高校範囲を超えてしまうがオイラーがとった方法を簡単に紹介しよう。

sinxは、マクローリン展開(大学1年で学習)により、次のような無限和で表される。(これはこれで驚きだが)

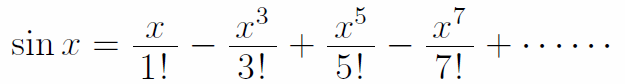
両辺をxで割ると

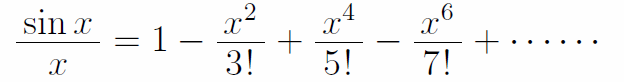
一方、sinx/xを別の形で表すことができる。sinx/xは、x=±π、±2π、±3π、……を代入するとsinx/x=0となるから、次のように因数分解できる。「f(x)にx=α、βを代入して0になるとき、f(x)が(α-x)(β-x)つまり(1-x/α)(1-x/β)を因数にもつ」と同様である。ここで、有限の話が無限の場合にも成立するかという問題が生じるがとりあえず無視する。

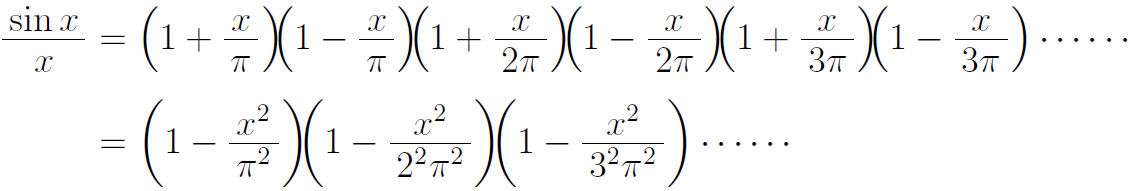
ここで、2通りに表されたsinx/xのそれぞれの式のx²の係数を取り出して等式を作ると

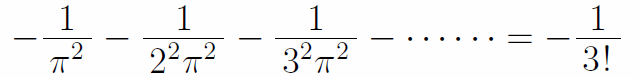
両辺に-π²を掛けて

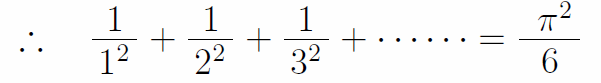
このように少し乱暴ではあるものの、オイラーは非常に強い直感力と洞察力で平方数の逆数の無限和が(円周率の2乗)÷6に一致することを初めて発見したのである。オイラーはこのときのことを「エレガントな公式が見つかった」と記している。

驚くべき結果である。平方数の逆数を無限に足し合わせたものが、円周率の2乗を完全数の6で割った値と一致するというのである。

オイラーは、この結果に満足せずさらなる追求を続け、以下のように左辺の無限和を書き換えられることを発見した。

例として、次のように分母が素数の2と3と5であるような無限和の積を作成して展開してみると、2と3と5で作られる全ての合成数の逆数の無限和ができる。分母に2、3、5以外の素数(7,11,13・・・)やその合成数が表れることはない。

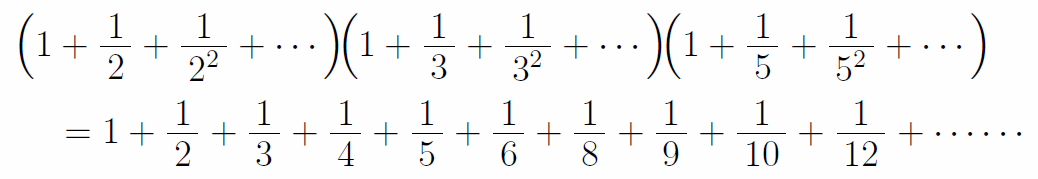
ここで、左辺の1つ1つの括弧内は無限等比級数(数Ⅲ)であるから、次のように変形できる。

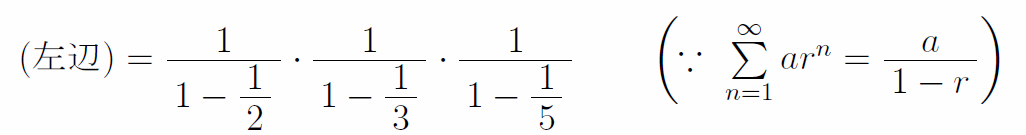
これを一般化し、全ての素数の無限和の積を作成して展開すると、全ての自然数の逆数の無限和ができる。この素数のみで作られた積をオイラー積という。

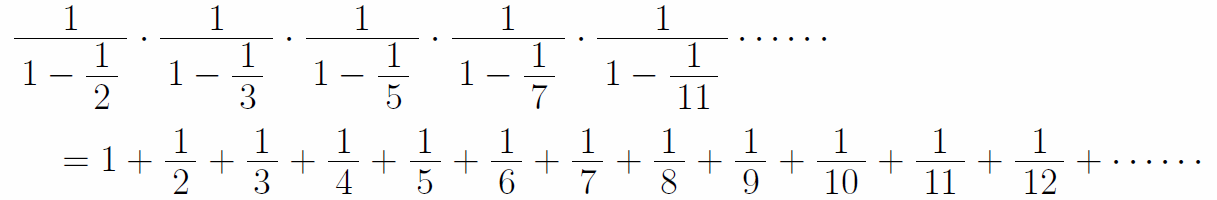
つまり、全ての自然数の逆数の無限和は全ての素数だけの数列の無限積で表すことができるのである。同じことを2乗で行えば

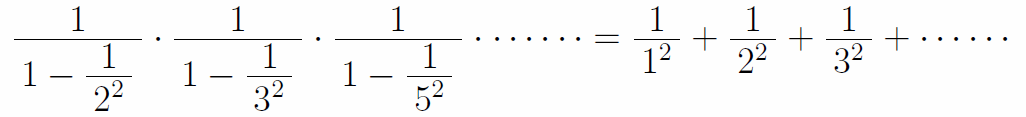
結局、先の結果と併せると次の等式が成立する。左辺は無限に存在する全ての素数を1つ残らず用いて作られた式である。

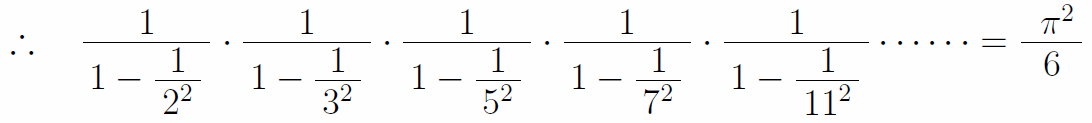
全く規則性が見えなかった素数だが、全て集めてみると自然界で最も美しい形である円を表す円周率が表れるのだ。かくして、オイラーは円周率πを介在することで、素数の中に何らかの調和性があること、自然と素数が全くの無関係ではないことを人類史上初めて示した人物となったのである。

ガウスが発見した素数定理

オイラーに続いて素数に隠された規則性に気付いたのは、19世紀最大の数学者ガウスである。

ガウスもまた素数の配列には何らかの意味があるはずだと考えていた。しかし、長年にわたって多くの数学者が素数の生成公式を見つけようとしては失敗してきたという事実から、そろそろ別の観点から考えてみてもよいだろうと当時15歳の少年ガウスは考えていた。

この前年、ガウスは人から対数表と素数表の両方が載っている本をもらっていた。計算機がない時代、商人や航海士は当たり前のように対数表をもっていた。巨大な数の計算を容易に行うためである。一方で、素数表は実生活には応用できない無意味なものであった。

ガウスはその素数表のほうに虜になった。対数の動きが予想できるのに対し、素数の動きは不規則だった。

ガウスは素数が表れるタイミングを正確に予測しようというこれまでのアプローチを止め、ある特定の範囲内の素数の個数を予想できないかと考えた。素数が存在する割合を調べていったガウスは、それが対数表と関連していることに気付いた。

1792年、15歳のガウスは1から自然数xまでの数の中に存在する素数のおおよその個数が次の式で与えられることを発見した。この「素数定理」が証明されたのはガウスが予想してから100年以上経過した1896年のことであった。ここで、π(x)は素数の個数を意味するものであり、円周率のπとは無関係であることに注意して欲しい。

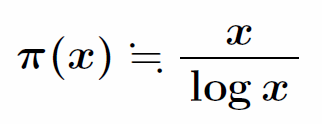
対数は自然界にも頻繁に現れる。銀河や台風やアンモナイトなどに見られるような渦巻きは対数螺旋(極座標表示 r=ae^bθ)と呼ばれるものである。

素数定理は、素数の個数がπと並んで自然界における重要な定数である自然対数の底eと密接に関係していることを示唆する。ガウスは自然対数の底eを介在することで、自然と素数が関連していることに気付いたのである。

素数が自然界における2大定数円周率πと自然対数の底eに関連しているという事実は、素数が自然界の重要な構成要素であることを示唆している。

ちなみに現代の素数表はこれ。

ところどころに小ネタがちりばめられており、なかなか面白い(気付いた？)。1は素数ではない。最初の000001は順番を表しているだけである。

世界で最も美しい等式

ガウスが素数と自然対数の底eの関連性に気付く45年前、オイラーは円周率πと自然対数の底eの不思議な関係式を発見していた。

このオイラーの公式と呼ばれる等式は、π、e、iという別分野で誕生した定数を仲立ちとして指数関数と三角関数を結びつけるものである。

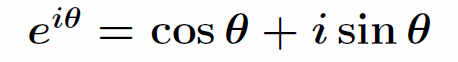
この等式にθ＝πを代入して=0とすると次の等式が得られる。

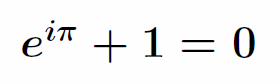
別々の分野で独立に発見された5大定数、円周率π(幾何学)、自然対数の底e(解析学)、虚数単位i(代数学)、和の単位元0(足しても元の数が変わらない)、積の単位元1(掛けても元の数が変わらない)が非常にシンプルにまとまっており、「世界で最も美しい等式」とも評される。

自然界に潜む2大定数のキングπとクイーンeは、i(愛)で結ばれていたのである。

未解決問題　リーマン予想

See page for author, Public domain, via Wikimedia Commons

あのガウスを師にもつベルンハルト・リーマン(ドイツ ; 1826-1866)は、素数の研究を行う過程でオイラーが研究していた以下の級数を複素数全体にまで拡張し、ζ(ゼータ)関数と名付けた。s=(整数)を考えていたオイラーに対し、s=(全ての複素数)で考えることにしたのである。

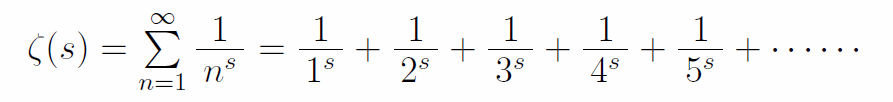
このゼータ関数のゼロ点(ζ(s)=0となるような複素数s)が素数の並びと関連していることに気付いたリーマンは、自明なゼロ点(負の偶数)以外のゼロ点の位置を求め始めた。

4個ほどゼロ点を求めてみると、複素平面において全てが一直線上(実部が1/2)に並んでいた。このとき、リーマンは完全に無秩序に散らばっていた素数がゼータ関数というフィルターを通して見ると高い秩序を保った姿に変わることに気付いたのである。

この4つのゼロ点だけが偶然並んでいるわけではなく、無数にあるゼロ点が全て一直線上にあるはずだという予想がいわゆる「リーマン予想」である(1859年)。

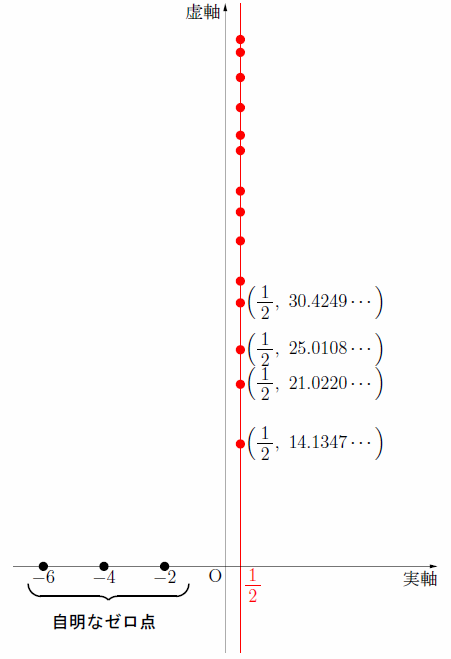
リーマンの功績は「素数の配列に規則性はあるか」という漠然とした問いを「自明でないゼロ点は一直線上にあるか」という数学の問題に帰着させたことにある。

この問題はリーマンの予想から150年以上経過しても未解決のままであり、数学における最重要問題の1つとなっている。コンピュータを用いてゼロ点を10兆個まで求めても全く反例が見つからないことから、多くの数学者は正しいと信じており、既にリーマン予想が正しいという仮定の下数千の論文が発表されている。

リーマン予想と量子物理学とのつながり

時は流れ、1970年頃、ヒュー・モンゴメリー(アメリカ)はリーマン予想とは別の問題の解決のために、ゼロ点の間隔に着目し調べ始めた。

当初、素数が無秩序であるのと同様、素数で作られるゼータ関数のゼロ点の間隔も無秩序であるはずだと考えていた。ところが、実際に調べてみると予想に反してゼロ点の間隔は完全に均一に散らばっているようだった。モンゴメリーは間隔の分布をグラフにしてみたが、予想とは正反対の結果にその意味をとらえきれずにいた。

1972年、プリンストン高等研究所に立ち寄ったモンゴメリーは物理学者フリーマン・ダイソン(アメリカ；1923-2020)と話す機会を得た。それは研究所で日常になっているティータイムの間の軽い会話のはずだったが、モンゴメリーがゼロ点の間隔を表す数式について話し始めたとき、ダイソンの顔つきが変わった。

「それは重い原子核のエネルギー準位の間隔を表す式と同じじゃないか」

数の原子ともいえる素数の間隔と自然や宇宙を構成する原子がもつエネルギーの間隔には密接な関連があったのだ。

この2人の奇跡の巡り合わせは神から人類への贈り物であったのだろうか。

人類は素数と自然界との真に深いつながりを発見した。リーマン予想の証明にもつながる素数の謎は、もはや数学者だけの挑戦ではなくなり、物理学者も含めて人類が力を結集して解明すべきものになったのである。

人類は素数と共に

リーマン予想には、2000年にアメリカのクレイ研究所によって100万ドルの懸賞金が懸けられた(ミレニアム懸賞問題)。

かつて、素数は物好きな人間の好奇心の対象でしかなく、実際には何の役にも立たないと考えられていた。しかし、今やインターネット通信の安全性が巨大な素数を用いた暗号によって保証されているように、素数は我々が暮らす現代社会と切っても切り離せいない関係になっている。

リーマン予想が証明されるとき、人類はまた新たな一歩を踏み出すことになるのかもしれない。

最後に

当ページの記述は、主に2009年にNHKで放送された次の放送を元にしている。この番組はBSで何度か再放送されている。

その他、以下の書籍やサイトも参考にした。そもそもNHKの番組は「素数の音楽」を元にしている。

リーマン予想(Wikipedia)

レオンハルト・オイラー(Wikipedia)

カール・フリードリヒ・ガウス(Wikipedia)

ベルンハルト・リーマン(Wikipedia)

 
NHKスペシャルではリーマン予想以外にも、ポアンカレ予想(1904年にポアンカレ(フランス)が予想し、2003年ペレルマン(ロシア)が証明)を特集した「100年の難問はなぜ解けたのか ～天才数学者 失踪の謎～」や、「神の数式」(すべての自然現象を1つの数式だけで説明しようとする物理学者達の戦いの歴史；下に示した全4回)についても放送されている。

第1回 この世は何からできているのか~美しさの追求 その成功と挫折~
第2回 “重さ”はどこから生まれるのか~自発的対象性の破れ 驚異の逆転劇~
第3回 宇宙はなぜ始まったのか~残された“最後の難問”~
第4回 異次元宇宙は存在するか~超弦理論“革命”~