

一見すると何の変哲もないごく普通の数Ⅲのグラフを図示して面積を求める問題のように思える。
とりあえず、基本通り微分して増減表を作成する。
より正確なグラフを図示するために最初は増減表にf”(x)とg”(x)を含めるつもりであったが、実際に計算してみるとg”(x)=0が求められないので必要ないと判断した。また、結果の形を考慮するとf'(x)とg'(x)の片側極限を求めておくべきである。
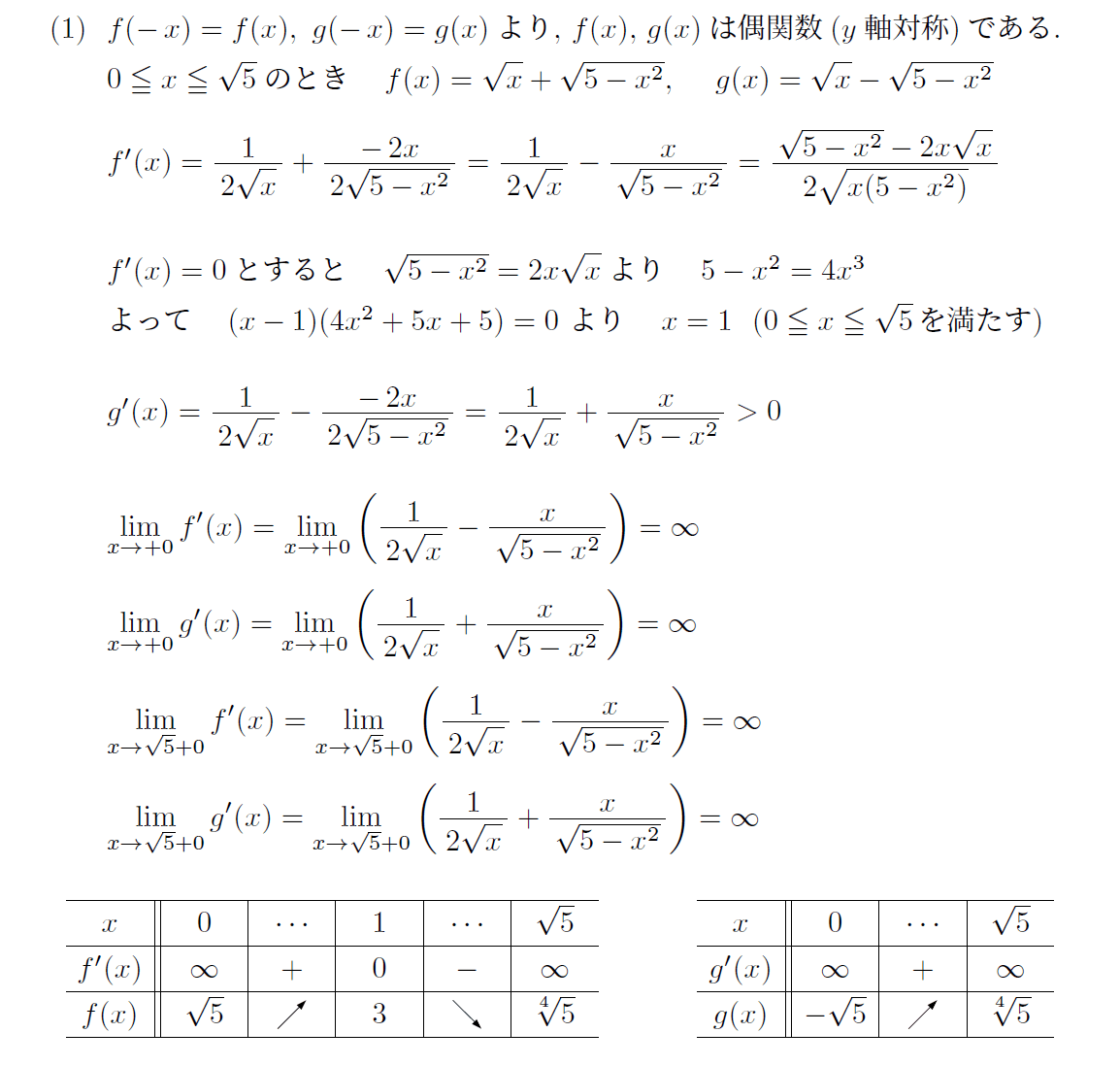
増減表を元にグラフを図示してみると・・・・・・
片側極限計算から、f(x)、g(x)ともに端点ではy軸と平行になることに注意して図示している。
特別に中身をピンクで塗りつぶしたよ♥
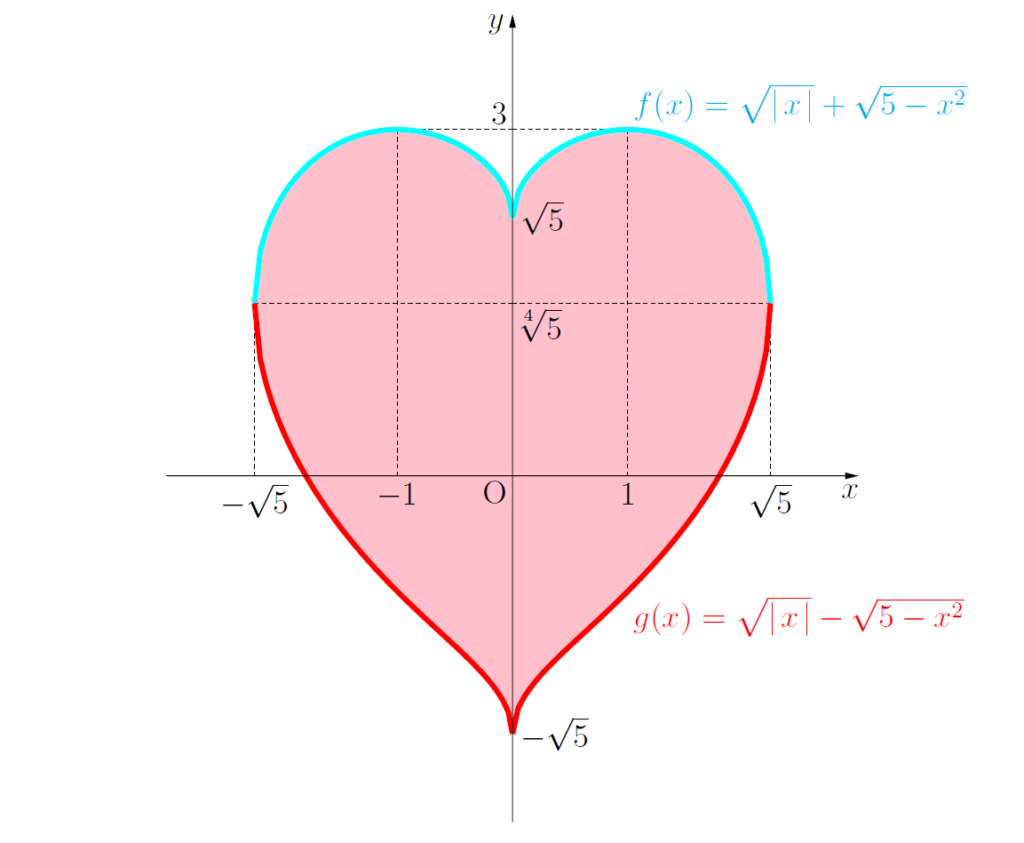
これはもしや・・・大学から受験生へのラブコール・・・・・・
しっかりと受け止めることが出来た受験生だけが、大学と4年間を共にすることができた。
2012年2月25日が記念すべき愛の告白記念日である。

素晴らしい問題である。何も結果がハートだからというだけではない。
試験時間内に完答するには、正確な微分計算はもちろんのこと、グラフを書くときのポイント(対称性・極限)を的確に把握して図示しなければならない。
また、積分計算なしで面積を求める方法を習得していることが望ましい。
受験数学の微分法・積分法における重要ポイントを多数含み、受験生にとって適度な計算量や難易度であるという意味でかなりの良問である。
実際にやってみると簡単ではなく、2000年静岡大学の問題と同様に受験勉強の際に一度はチャレンジしておいてほしい問題である。
ハートの形になる関数は他にもいろいろあるので、興味がある人は検索してみるとよいだろう。


