
暗記数学
何と美しい響きの言葉だろうか。
暗記数学とは、1980年代に受験アドバイザーの和田秀樹氏(灘中高→東大医学部)によって提唱された数学学習法である(Wikipediaより)。
ネット上では、この暗記数学の是非が度々話題になる。
しかし、普段指導する生徒の偏差値が50だったり70だったりなど、立場が大きく異なる教師達が異なるニュアンスで「暗記数学」という言葉を用いていたりするため、議論がきちんと噛み合っているのをみた試しがない。
いずれにせよ暗記数学とは「解法の暗記」という意味合いで用いるのが普通であり、社会の年号のように「答えの数字の丸暗記」という意味合いで用いる人はいまい。
そこで今回、自分は答えの数字だけを丸暗記する新たな数学学習法「丸暗記数学」を提唱しようと思う。
そんなの意味ある?
あった!!!
バーゼル問題
2014年頃、いわゆるバーゼル問題を背景に持つ日本女子大学の2003年の問題を紹介した。
バーゼル問題とは、「平方数の逆数の無限和を求めよ」という問題であり、1644年にスイスのバーゼル在住のベルヌーイによって提起され、1735年に伝説の数学者レオンハルト・オイラーによって解決された。
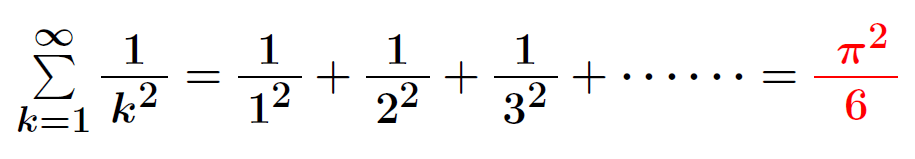
平方数の逆数を無限に足し合わせたものが、円周率の2乗を完全数の6で割った値と一致するという驚くべき結果である。
現在は高校範囲での証明も知られているが、難易度が高く大学入試の題材となることは極めて稀なので、伝説の入試問題として取り上げたわけである。
Jakob Emanuel Handmann, Public domain, via Wikimedia Commons
レオンハルト・オイラーは、歴史上最も偉大な数学者の1人であり、18世紀最大の数学者である。
ニュートンが数学を自然界に応用し多くの科学的な実績を残していた18世紀初頭、オイラーはスイスのバーゼルで誕生した。
1720年、わずか13歳にしてバーゼル大学に入学して哲学を学んだが、スイスで有名な数学者一族ベルヌーイ家のヨハン・ベルヌーイに数学の才能を見い出された。1735年にバーゼル問題を解決したことで一目置かれる存在になる。
オイラーは、人間離れした計算力と記憶力で膨大な計算を暗算で行うことができた。8桁同士の掛け算を数秒、寝付けなかったときには100までの整数の6乗を暗算していたなど、伝説的エピソードに事欠かない。
数学のあらゆる分野に基礎から応用まで、さらには物理学にも膨大な業績を残した。オイラーの公式、オイラー定数、オイラー方程式、オイラー関数、オイラー予想、オイラー近似、一筆書きができる必要十分条件(オイラーグラフ)、オイラー線、オイラーの多面体公式、オイラーの運動方程式など、様々な分野で頻繁にオイラーの名が登場する。他の数学者の名を冠していても実はオイラーの貢献による業績も多い。また、π、sin、cos、i、e、Σ、y=f(x)、三角形の角Aの対辺のaなど現在世界中で使用されている記号を普及させた。さらには、幾何学で表現されていたニュートン力学を「ma=F」という現在の解析的表現に変更したのもオイラーである。当時まだ市民権を得られていなかった虚数iを積極的に活用してその有用性を広めた功績も大きい。数学者には珍しく、学生に研究成果を平易に解説することにも長けており、教育者としても優秀であった。
非常に温厚で性格で、膝の上で子守をしながら論文を執筆していたとされる。国家に対しても従順で、暦の作成、硬貨の鋳造、運河の設置、水道の設計、大砲の改良、航海表の作成など様々な問題を解決した。
悪環境やストレスから、30歳になる頃には片目を、60歳になる頃には両目を失明してしまうが、論文を書くペースは全盲になっても全く変わることはなく、1783年に76歳で亡くなるその日まで数学に没頭していたという。
オイラーは1年間に普通の数学者の一生分に相当する平均800ページもの論文を書いたため、人類史上最も多くの論文を書いた数学者である。オイラーの論文は5万ページを超える全集にまとめられて1911年から刊行され続けているが、その全集は100年以上たった今日でも完結していない。
2018年東海大学医学部と2020年慶應義塾大学医学部の入試問題
2018年、東海大学医学部の入試において以下のような問題が出題された。

さらに2020年、私立大学医学部最難関の慶應義塾大学医学部入試で以下の出題がなされた。

いずれもかなり前置きが長いが、一番最後はバーゼル問題に他ならない。
特筆すべきは、私立大学故の穴埋め形式の試験だったことである。
つまり、結果を覚えてさえいれば
瞬殺!!!
細かい配点は不明だが、おそらく5点くらいか。
1点を争う熾烈な医学部受験において、ノータイムで約5点稼げるのはめっちゃデカイ。
自分が最初に記事にしたときは、バーゼル問題を取り扱っているサイトは少なかったように記憶しているが、今では多くのサイトやYouTubeでも紹介されており、医学部受験生ともなれば事前に知っていた人も少なくないだろう。
バーゼル問題の結果はシンプルで美しくインパクトがあるのでチラッと見ただけでも記憶に残りやすい。
途中が出来ていないのになぜか最後だけ合っていた答案もそれなりにあったのではないか。
伝説の知識が合否を分けた・・・かも・・・。
自分が受験生だったならば、「バーゼル問題キタ━━゚+.ヽ(≧▽≦)ノ.+゚━━ ッ ! ! !」などと興奮して合否がどうでもよくなりそう(笑)。
以下に解答を示す。2003年の日本女子大学の問題は数Ⅲの微分積分を利用するかなり難解な方法であったが、東海大学と慶應義塾大学の問題は極限以外は数ⅡBの範囲である。特に慶應義塾大学の問題ではこんな簡単にバーゼル問題が解決できることに驚いた。
(4),(5)は初見だと難しい。
本質的に同じ問題は大学入試で散見され、特に2016年の横浜市立大学の出題は伝説である。

数式は仰々しいが、本質的に難しいところはない。
受験生のレベルを考慮するとやや易~標準である。
時間的な余裕があるわけではないので、最後を瞬殺できればかなり有利になる。
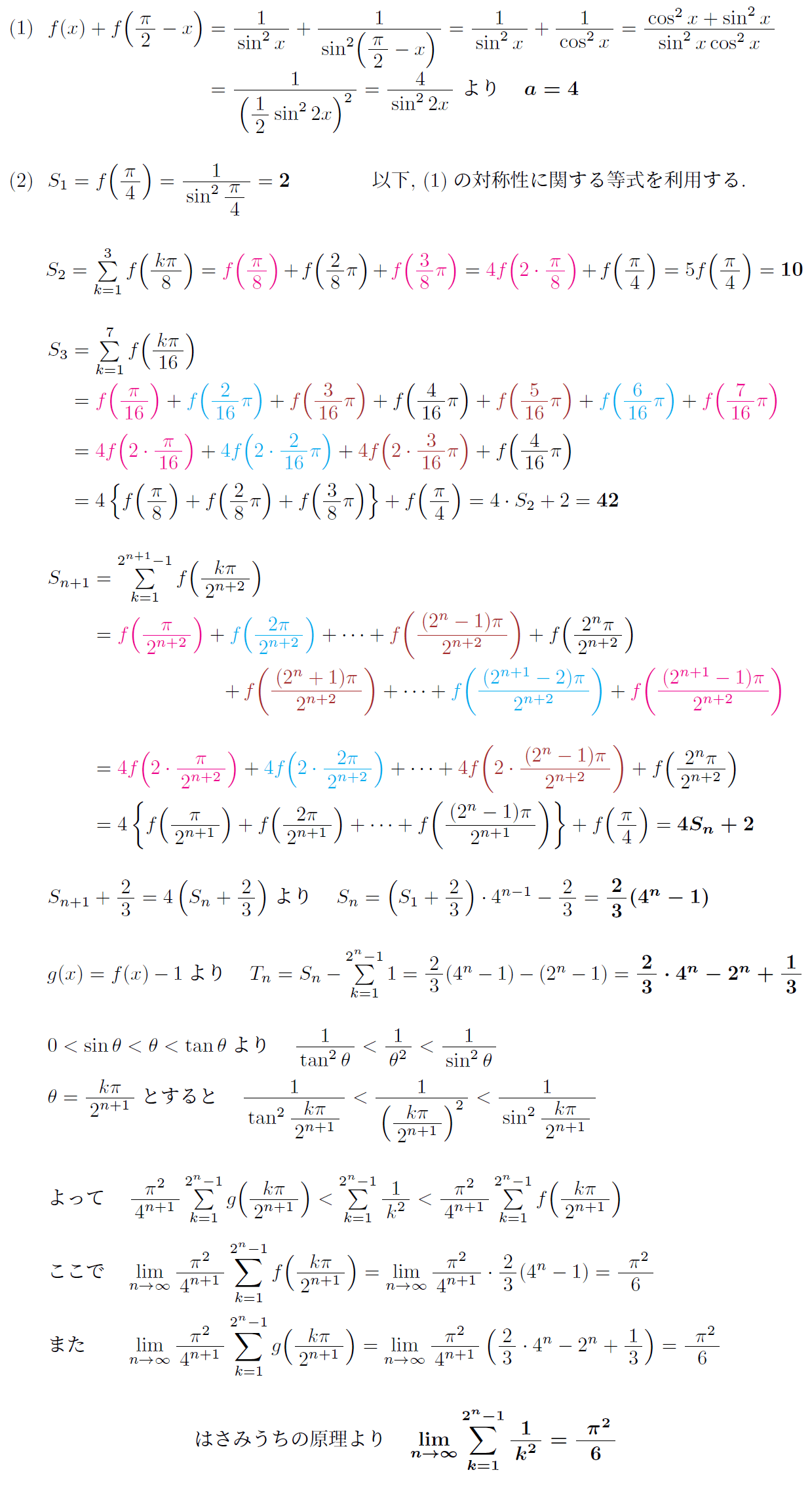
このように、単に過去問演習するなど普通の受験勉強をしているだけでなく、普段から広範囲にアンテナを張り巡らせておくと、運良く本番でぶちかませるかもしれないのだ。
仮に記述試験であっても、白紙よりはマシなので、結果を覚えていたならばそれだけでも書いておくことができる。他の受験生の出来次第では何点かもらえる可能性がある。
これが丸暗記数学だ!!!
丸暗記前提の私立大学入試問題
特に穴埋め形式の多い私立大学入試においては、丸暗記が役立つどころかそもそも丸暗記前提と思われる問題も出題される。

この2018年の産業医科大学医学部の問題は、第1問の小問7つのうちの1つであり、時間的観点からも正攻法が完全数の暗記といっても差し支えないだろう。
完全数は小さい順に並べると以下となるが、496くらいまでは常識としておきたい。
6、28、496、8128、33550336、・・・・・・
出題者の立場に立ってみれば、何らかの背景がある問題の方が出題がしやすい。変にオリジナリティのある問題を出題すると、後から問題の不備を指摘されて「全員に点数を与える」などと面倒なことをする羽目になったりするからである。
余談だが、「次に大きい」という日本語の意味合いが度々ネット上で議論の対象になる。
「5」の次に大きい素数は?
この質問の答えが「3」と「7」のどちらかで意見が分かれるのである。
また、次の質問についてはどうだろうか。
身長が以下の3人のうち、Bの次に大きい人は?
| A | 150cm |
| B | 160cm |
| C | 170cm |
「次」を順位的な意味合いでとらえるか数列的な意味合いでとらえるかだと思うが、これといった明確な決まりはないようで、「次に大きい」という表現を使う際は誤解を生まないように注意した方が良さそうである。




