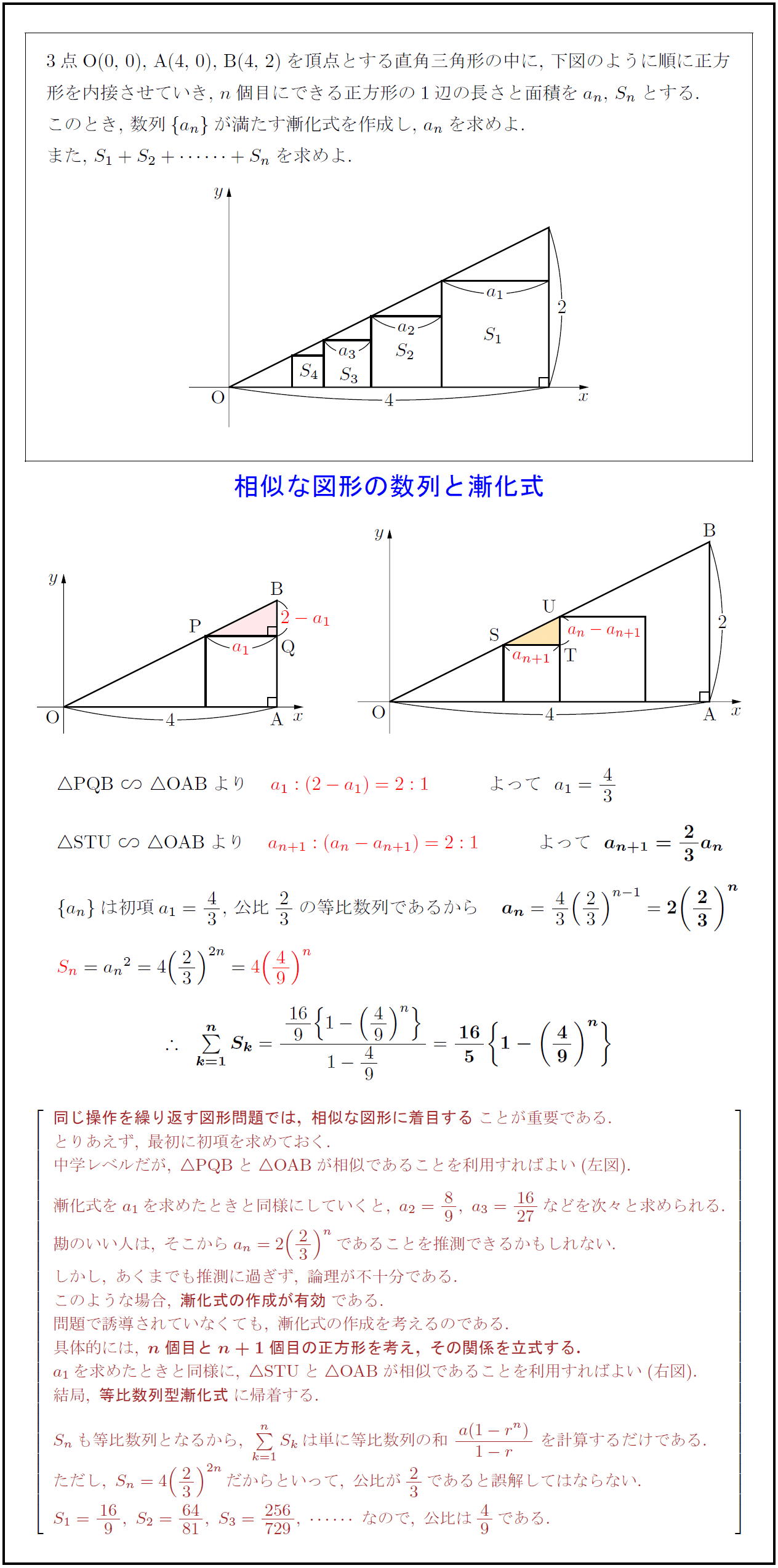
3点O(0,\ 0),\ A(4,\ 0),\ B(4,\ 2)を頂点とする直角三角形の中に,\ 下図のように順に正方 形を内接させていき,\ $n$個目にできる正方形の1辺の長さと面積を$a_n$,\ $S_n$とする. このとき,\ 数列${a_n}$が満たす漸化式を作成し,\ $a_n$を求めよ. {同じ操作を繰り返す図形問題では,\ 相似な図形に着目する}ことが重要である. とりあえず,\ 最初に初項を求めておく. 中学レベルだが,\ {PQB}と{OAB}が相似であることを利用すればよい(左図). 漸化式をa₁を求めたときと同様にしていくと,\ a₂=89,\ a₃={16}{27}などを次々と求められる. 勘のいい人は,\ そこからa_n=2(23)^nであることを推測できるかもしれない. しかし,\ あくまでも推測に過ぎず,\ 論理が不十分である. このような場合,\ {漸化式の作成が有効}である. 問題で誘導されていなくても,\ 漸化式の作成を考えるのである. 具体的には,\ {n個目とn+1個目の正方形を考え,\ その関係を立式する.} a₁を求めたときと同様に,\ {STU}と{OAB}が相似であることを利用すればよい(右図). 結局,\ {等比数列型漸化式}に帰着する. S_nも等比数列となるから,\ ΣS_kは単に等比数列の和\ {a(1-r^n)}{1-r}\ を計算するだけである. ただし,\ S_n=4(23)^{2n}だからといって,\ 公比が23であると誤解してはならない. S₁={16}{9},\ S₂={64}{81},\ S₃={256}{729},なので,\ 公比は49である.

