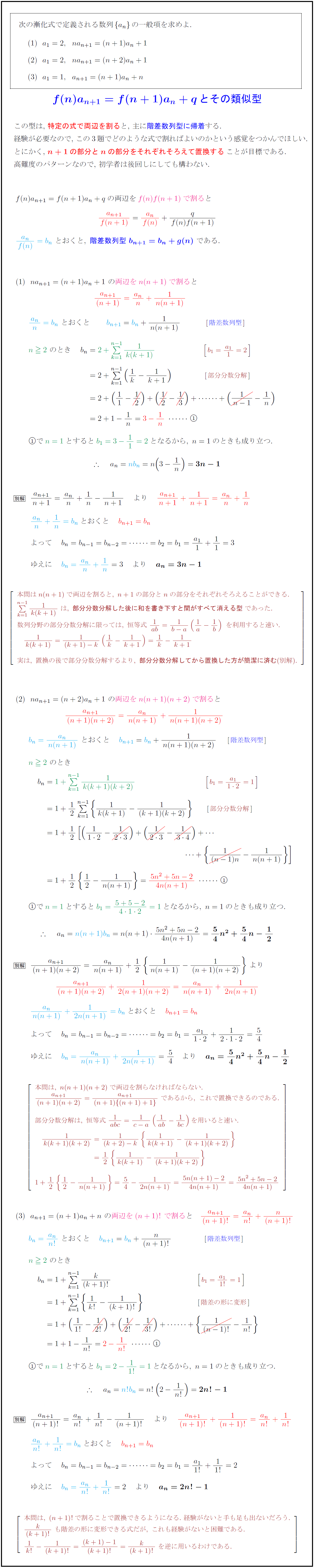
次の漸化式で定義される数列a_n}の一般項を求めよ.$ $ a₁=2,na_{n+1}=(n+1)a_n+1$ $ a₁=2,na_{n+1}=(n+2)a_n+1$ $ a₁=1,a_{n+1}=(n+1)a_n+n$ f(n)a_{n+1}=f(n+1)a_n+qとその類似型$ この型は,\ 特定の式で両辺を割ると,\ 主に階差数列型に帰着する. 経験が必要なので,\ この3題でどのような式で割ればよいのかという感覚をつかんでほしい. とにかく,\ ${n+1の部分とnの部分をそれぞれそろえて置換することが目標である.$ 高難度のパターンなので,\ 初学者は後回しにしても構わない. $f(n)a_{n+1}=f(n+1)a_n+q$の両辺を$f(n)f(n+1)$で割る}と 本問はn(n+1)で両辺を割ると,\ n+1の部分とnの部分をそれぞれそろえることができる. n-1}{1}{k(k+1)}\ は,\ {部分分数分解した後に和を書き下すと間がすべて消える型}であった. 数列分野の部分分数分解に限っては,\ 恒等式\ {1}{ab}={1}{b-a}(1a-1b)\ を利用すると速い. 実は,\ 置換の後で部分分数分解するより,\ {部分分数分解してから置換した方が簡潔に済む}(別解). 本問は,\ (n+1)!で割ることで置換できるようになる.\ 経験がないと手も足も出ないだろう. {k}{(k+1)!}\ も階差の形に変形できる式だが,\ これも経験がないと困難である. \

