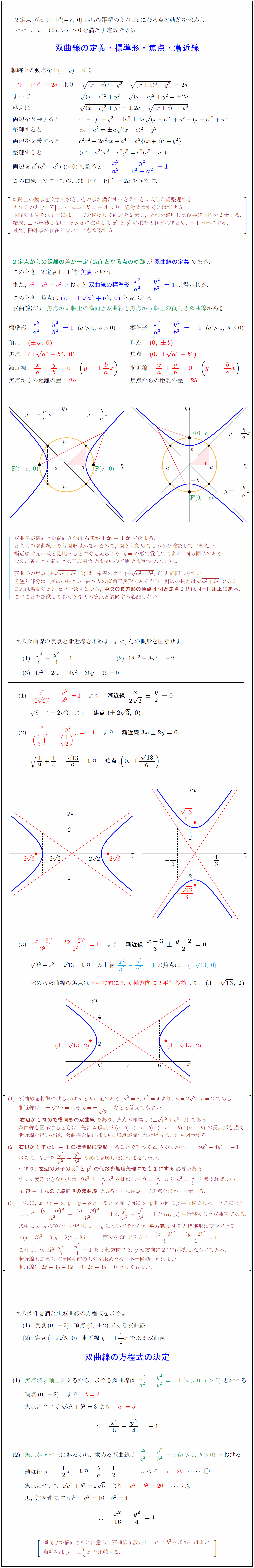
2定点F$(c,\ 0)$,\ F$'(-c,\ 0)$からの距離の差が$2a$になる点の軌跡を求めよ. ただし,\ $a,\ cは$を満たす定数である. 軌跡上の動点をP$(x,\ y)$とする. ${PF}-{PF}’}=2a}より{(x-c)²+y²}-{(x+c)²+y²=2a$ $よって \ {(x-c)²+y²}-{(x+c)²+y²}=2a$ $ゆえに \ {(x-c)²+y²}=2a+{(x+c)²+y²}$ $両辺を2乗すると (x-c)²+y²=4a²4a{(x+c)²+y²}+(x+c)²+y²$ $整理すると \ cx+a²=a{(x+c)²+y²}$ $両辺を2乗すると c²x²+2a²cx+a⁴=a²{(x+c)²+y²}$ $整理すると \ (c²-a²)x²-a²y²=a²(c²-a²)$ $両辺をa²(c²-a²)\ (0)で割ると x²}{a²}-{y²}{c²-a²}=1$ $この曲線上のすべての点は\ {PF}-{PF}’}=2a\ を満たす.$ $[l} 軌跡上の動点を文字でおき,\ その点が満たすべき条件を立式した後整理する. A0のとき\ X}=AX=A\ より,\ 絶対値はすぐにはずせる. 本問の根号をはずすには,\ 一方を移項して両辺を2乗し,\ それを整理した後再び両辺を2乗する. 結局,\ の影響はない.caに注意してx²とy²の項をそれぞれまとめ,\ =1の形にする. 最後,\ 除外点が存在しないことも確認する. }]$ ${2定点からの距離の差が一定(2a)となる点の軌跡が{双曲線の定義である.$ $このとき,\ 2定点{F,\ F}’を{焦点という.$ $また,\ c²-a²=b²}\ とおくと{双曲線の標準形\ {x²}{a²}-{y²}{b²}=1\ が得られる.$ $このとき,\ 焦点は\ {(c={a²+b²},\ 0)\ と表される.$ $双曲線には,\ 焦点がx軸上の横向き双曲線}と焦点がy軸上の縦向き双曲線}がある. $漸近線 { xa yb=0 ({y= bax)$ $焦点からの距離の差 {2a$ $焦点からの距離の差 {2b$ 双曲線が横向きか縦向きかは{右辺が1か-1か}で決まる. どちらの双曲線かで各図形量が変わるので,\ 図とも絡めてしっかり確認しておきたい. 漸近線は元の式と見比べるとすぐ覚えられる.\ y=の形で覚えてもよい.\ 両方同じである. なお,\ 横向き・縦向きは正式用語ではないので他では使わないように. 双曲線の焦点({a²+b²},\ 0)は,\ 楕円の焦点({a²-b²},\ 0)と混同しやすい. 色塗り部分は,\ 底辺の長さa,\ 高さbの直角三角形であるから,\ 斜辺の長さは{a²+b²}\ である. これは焦点のx座標と一致するから,\ {中央の長方形の頂点4個と焦点2個は同一円周上にある.} このことを認識しておくと楕円の焦点と混同する心配はない. 漸近線\ {x-3}{3}{y-2}{2}=0}$ ${3²+2²}={13} より 双曲線\ {x²}{3²}-{y²}{2²}=1}\ の焦点は ({13},\ 0)}$ $求める双曲線の焦点はx軸方向に3,\ y軸方向に2平行移動}して {(3{13},\ 2)}$ 双曲線を特徴づけるのはaとbの値である.\ a²=8,\ b²=4より,\ a=22,\ b=2\ である. 漸近線は\ x2y=0\ や\ y={1}{2}x\ などと答えてもよい. {右辺が1なので横向きの双曲線}であり,\ 焦点の座標は\ ({a²+b²},\ 0)\ である. 双曲線を図示するときは,\ 先に4頂点が(a,\ b),\ (-a,\ b),\ (-a,\ -b),\ (a,\ -b)\ の長方形を描く. 漸近線を描いた後,\ 双曲線を描けばよい.\ 焦点が問われた場合はこれも図示する. {右辺が1または-1の標準形に変形}することで初めてa,\ bがわかる. 9x²-4y²=-1 さらに,\ 左辺を\ {x²}{a²}+{y²}{b²}\ の形に変形しなければならない. つまり,\ {左辺の分子のx²とy²の係数を無理矢理にでも1にする}必要がある. すぐに変形できない人は,\ 9x²\ と\ {1}{a²}x²\ を比較して9={1}{a²}\ より\ a²=19\ と考えればよい. {右辺-1なので縦向きの双曲線}であることに注意して焦点を求め,\ 図示する. 一般に,\ x→x-α,\ y→y-βとするとx軸方向にα,\ y軸方向にβ平行移動したグラフになる. よって,\ (x-α)²}{a²}-{(y-β)²}{b²}=1}は{x²}{a²}-{y²}{b²}=1を(α,\ β)平行移動した双曲線である. 式中にx,\ yの項を含む場合,\ xとyについてそれぞれ{平方完成}すると標準形に変形できる. 4(x-3)²-9(y-2)²=36 両辺を36で割ると {(x-3)²}{9}-{(y-2)²}{4}=1 これは,\ 双曲線\ {x²}{9}-{y²}{4}=1\ をx軸方向に3,\ y軸方向に2平行移動したものである. 漸近線も焦点も平行移動前のものを求めた後,\ 平行移動すればよい. 漸近線は\ 2x+3y-12=0,\ 2x-3y=0\ としてもよい. 次の条件を満たす双曲線の方程式を求めよ. $焦点(0,\ 3),\ 頂点(0,\ 2)である双曲線.$ $焦点(25,\ 0),\ 漸近線\ y=12x\ である双曲線.$ 焦点がy軸上}にあるから,\ 求める双曲線は\ {x²}{a²}-{y²}{b²}=-1\ (a0,\ b0)}\ とおける.$ $頂点(0,\ 2) より b=2}$ $焦点について\ {a²+b²}=3\ より a²=5}$ $ x²}{5}-{y²}{4}=-1}$} $焦点がx軸上}にあるから,\ 求める双曲線は\ {x²}{a²}-{y²}{b²}=1\ (a0,\ b0)}\ とおける.$ $漸近線\ y=12x より ba=12 よって a=2b}$ $焦点について\ {a²+b²}=25 より a²+b²=20}$ $,\ を連立すると a²=16,b²=4$ $ x²}{16}-{y²}{4}=1}$} $[l} 横向きか縦向きかに注意して双曲線を設定し,\ a²とb²を求めればよい. 漸近線は\ y= bax\ と比較する.

