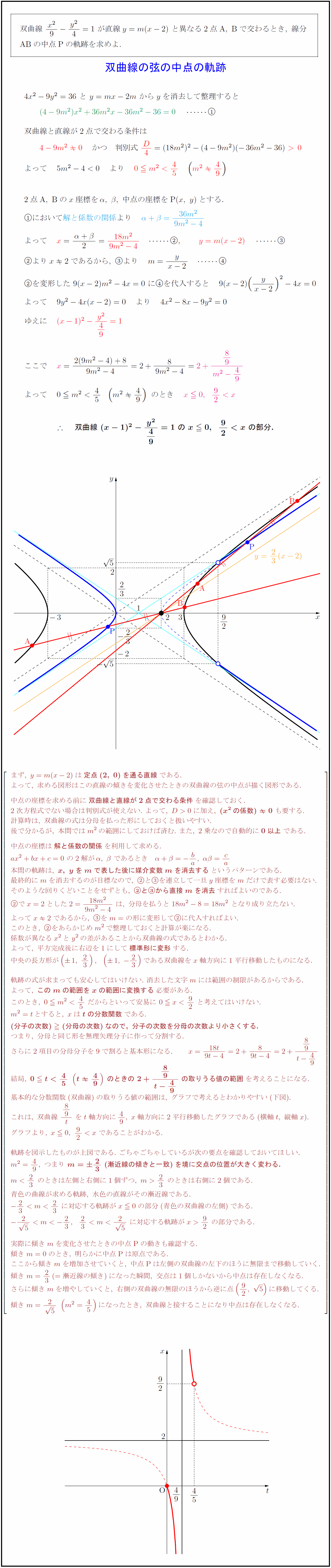
双曲線\ {x²}{9}-{y²}{4}=1\ が直線y=m(x-2)\ と異なる2点{A,\ B}で交わるとき,\ 線分$ ${AB}の中点{P}の軌跡を求めよ.$ $4x²-9y²=36\ と\ y=mx-2m\ からyを消去して整理すると$ $(4-9m²)x²+36m²x-36m²-36=0} $ $双曲線と直線が2点で交わる条件は$ $4-9m²0} かつ 判別式\ D4}=(18m²)²-(4-9m²)(-36m²-36)\ 0}$ $よって 5m²-4 0 m²{4}{5 (m²49})$ $2点{A,\ B}のx座標をα,\ β,\ 中点の座標を{P}(x,\ y)とする.$ $において解と係数の関係}より α+β={36m²}{9m²-4$ $よって x}={α+β}{2}={18m²}{9m²-4 , y=m(x-2)} $ $よりx2であるから,\ より m={y}{x-2} $ $を変形した\ 9(x-2)m²-4x=0\ にを代入すると 9(x-2)({y}{x-2})²-4x=0$ $よって 9y²-4x(x-2)=0 より 4x²-8x-9y²=0$ $ゆえに (x-1)²-{y²}{49}=1}$ $ここで x}={2(9m²-4)+8}{9m²-4}=2+{8}{9m²-4}=2+{89}{m²-49$ $よって 0 m²{4}{5}(m²49)\ のとき x0,92x}$ $ {双曲線\ (x-1)²-{y²}{49}=1\ の\ x0,92x\ の部分.}$} まず,\ y=m(x-2)は{定点(2,\ 0)を通る直線}である. よって,\ 求める図形はこの直線の傾きを変化させたときの双曲線の弦の中点が描く図形である. 中点の座標を求める前に{双曲線と直線が2点で交わる条件}を確認しておく. 2次方程式でない場合は判別式が使えない.\ よって,\ Dに加え,\ {(x²の係数)0}\ も要する. 計算時は,\ 双曲線の式は分母を払った形にしておくと扱いやすい. 後で分かるが,\ 本問ではm²の範囲にしておけば済む.\ また,\ 2乗なので自動的に{0以上}である. 中点の座標は{解と係数の関係}を利用して求める. ax²+bx+c=0\ の2解がα,\ β\ であるとき 本問の軌跡は,\ {x,\ yをmで表した後に媒介変数mを消去する}というパターンである. 最終的にmを消去するのが目標なので,\ とを連立して一旦y座標をmだけで表す必要はない. そのような回りくどいことをせずとも,\ {とから直接mを消去}すればよいのである. でx=2とした2={18m²}{9m²-4}\ は,\ 分母を払うと18m²-8=18m²\ となり成り立たない. よってx2であるから,\ をm=の形に変形してに代入すればよい. このとき,\ をあらかじめm²で整理しておくと計算が楽になる. 係数が異なるx²とy²の差があることから双曲線の式であるとわかる. よって,\ 平方完成後に右辺を1にして{標準形に変形}する. 中央の長方形が(1,\ 23),(1,\ -23)である双曲線をx軸方向に1平行移動したものになる. 軌跡の式が求まっても安心してはいけない.\ 消去した文字mには範囲の制限があるからである. よって,\ {このmの範囲をxの範囲に変換する}必要がある. このとき,\ 0 m²45\ だからといって安易に\ と考えてはいけない. m²=tとすると,\ xは{tの分数関数}である. {(分子の次数)(分母の次数)なので,\ 分子の次数を分母の次数より小さくする.} つまり,\ 分母と同じ形を無理矢理分子に作って分割する. [-.5zh] さらに2項目の分母分子を9で割ると基本形になる. ] 結局,\ (t49)のときの\ 2+{89}{t-49}\ の取りうる値の範囲}を考えることになる. 基本的な分数関数(双曲線)の取りうる値の範囲は,\ グラフで考えるとわかりやすい(下図). これは,\ 双曲線\ {89}{t}\ をt軸方向に49,\ x軸方向に2平行移動したグラフである(横軸t,\ 縦軸x). グラフより,\ であることがわかる. 軌跡を図示したものが上図である.\ ごちゃごちゃしているが次の要点を確認しておいてほしい. m²=49,\ つまり\ {m=23\ (漸近線の傾きと一致)を境に交点の位置が大きく変わる.} のときは左側と右側に1個ずつ,\ 23\ のときは右側に2個である. 青色の曲線が求める軌跡,\ 水色の直線がその漸近線である. に対応する軌跡がx0の部分(青色の双曲線の左側)である. -{2}{5}-23,23{2}{5}\ に対応する軌跡が\ の部分である. 実際に傾きmを変化させたときの中点{P}の動きも確認する. 傾きm=0のとき,\ 明らかに中点{P}は原点である. ここから傾きmを増加させていくと,\ 中点{P}は左側の双曲線の左下のほうに無限まで移動していく. 傾きm=23(=漸近線の傾き)になった瞬間,\ 交点は1個しかないから中点は存在しなくなる. さらに傾きmを増やしていくと,\ 右側の双曲線の無限のほうから逆に点(92,\ 5)に移動してくる. 傾きm={2}{5}\ (m²=45)になったとき,\ 双曲線と接することになり中点は存在しなくなる.

