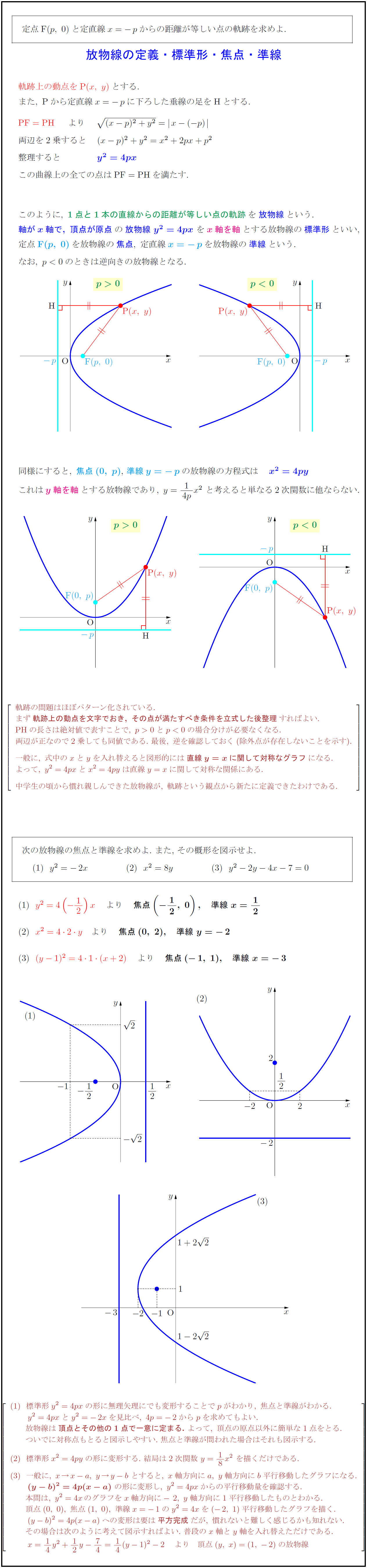
定点F$(p,\ 0)$と定直線$x=-p$からの距離が等しい点の軌跡を求めよ. [-.8zh] { 放物線の定義・標準形・焦点・準線 $軌跡上の動点を{P}(x,\ y)}とする.$ $また,\ {P}から定直線x=-pに下ろした垂線の足を{H}とする.$ ${PF}={PH \ より\ {(x-p)²+y²}=x-(-p)}$ $両辺を2乗すると (x-p)²+y²=x²+2px+p²$ $整理すると {y²=4px$ $この曲線上の全ての点は{PF=PH}を満たす.$ $このように,\ {1点と1本の直線からの距離が等しい点の軌跡を{放物線という.$ ${軸がx軸で,\ 頂点が原点の{放物線\ {y²=4px\ を{x軸を軸とする放物線の{標準形といい,$ $定点F}(p,\ 0)を放物線の{焦点,\ 定直線{x=-pを放物線の{準線という.$ $なお,\ p0のときは逆向きの放物線となる $同様にすると,\ 焦点}(0,\ p)$,\ ${準線y=-p$の放物線の方程式は ${x²=4py$ $これは{y軸を軸とする放物線であり,\ y={1}{4p}x²\ と考えると単なる2次関数に他ならない.$ 軌跡の問題はほぼパターン化されている. まず{軌跡上の動点を文字でおき,\ その点が満たすべき条件を立式した後整理}すればよい. {PHの長さは絶対値で表すことで,\ の場合分けが必要なくなる.} 両辺が正なので2乗しても同値である.\ 最後,\ 逆を確認しておく(除外点が存在しないことを示す). 一般に,\ 式中のxとyを入れ替えると図形的には{直線y=xに関して対称なグラフ}になる. よって,\ y²=4pxとx²=4pyは直線y=xに関して対称な関係にある. 中学生の頃から慣れ親しんできた放物線が,\ 軌跡という観点から新たに定義できたわけである. y²=4(-12)x} より {焦点(-12,\ 0), 準線\ x=12}$ $x²=42 y} より {焦点(0,\ 2), 準線\ y=-2}$ $(y-1)²=41(x+2)} より {焦点(-1,\ 1), 準線\ y=-3}$ 標準形y²=4pxの形に無理矢理にでも変形することでpがわかり,\ 焦点と準線がわかる. y²=4pxとy²=-2xを見比べ,\ 4p=-2からpを求めてもよい. 放物線は{頂点とその他の1点で一意に定まる.}\ よって,\ 頂点の原点以外に簡単な1点をとる. ついでに対称点もとると図示しやすい.\ 焦点と準線が問われた場合はそれも図示する. 標準形x²=4pyの形に変形する.\ 結局は2次関数\ y=18x²\ を描くだけである. 一般に,\ x→x-a,\ y→y-b\ とすると,\ x軸方向にa,\ y軸方向にb平行移動したグラフになる. {(y-b)²=4p(x-a)}\ の形に変形し,\ y²=4pxからの平行移動量を確認する. 本問は,\ y²=4xのグラフをx軸方向に-2,\ y軸方向に1平行移動したものとわかる. 頂点(0,\ 0),\ 焦点(1,\ 0),\ 準線x=-1のy²=4xを(-2,\ 1)平行移動したグラフを描く. (y-b)²=4p(x-a)への変形は要は{平方完成}だが,\ 慣れないと難しく感じるかも知れない. その場合は次のように考えて図示すればよい.\ 普段のx軸とy軸を入れ替えただけである. x=14y²+12y-74=14(y-1)²-2 より 頂点(y,\ x)=(1,\ -2)の放物線

