接線の方程式の導出は数Ⅲの微分法の知識を要するので、未学習ならば飛ばしてもかまいません。
以下はGeoGebraによる作図です。自分でスライダーを動かしてみてください。自動再生もできます。
平行に入射した光線が同じタイミングで焦点に到達することを確認してください。
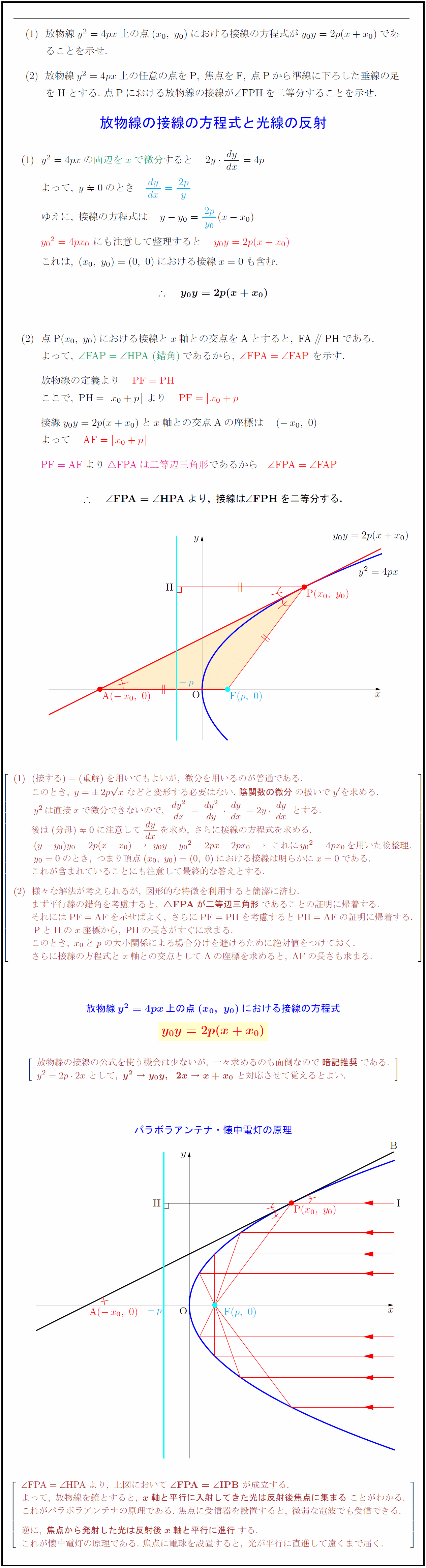
放物線y²=4px上の点(x₀,\ y₀)における接線の方程式がy₀y=2p(x+x₀)であ$ $ることを示せ.$ $放物線y²=4px上の任意の点を{P},\ 焦点を{F},\ 点{P}から準線に下ろした垂線の足$ $を{H}とする.\ 点{P}における放物線の接線が∠{FPH}を二等分することを示せ.$ 両辺をxで微分}すると 2y{dy}{dx}=4p$ $よって,\ y0のとき {dy}{dx}={2p}{y$ $ゆえに,\ 接線の方程式は y-y₀={2p}{y₀(x-x₀)$ ${y₀}²=4px₀}\ にも注意して整理すると y₀y=2p(x+x₀)}$ $これは,\ (x₀,\ y₀)=(0,\ 0)における接線x=0も含む.$ $ {y₀y=2p(x+x₀)}$} ${点P(x₀,\ y₀)における接線とx軸との交点をAとすると,\ FA∥ PHである.}$ ${よって,\ ∠ FAP=∠ HPA\ (錯角)}であるから,\ ∠ FPA=∠ FAP}\ を示す.}$ ${放物線の定義より PF=PH$ ${ここで,\ PH=x₀+p}\ より PF=x₀+p}$ ${接線y₀y=2p(x+x₀)とx軸との交点Aの座標は (-x₀,\ 0)}$ ${よって AF=x₀+p}$ ${PF=AF}より FPAは二等辺三角形}であるから ∠ FPA=∠ FAP$ $ ∠ FPA=∠ HPAより,\ 接線は∠ FPHを二等分する.$} (接する)=(重解)を用いてもよいが,\ 微分を用いるのが普通である. このとき,\ y=2p x\ などと変形する必要はない.\ {陰関数の微分}の扱いでy’を求める. y²は直接xで微分できないので,\ {dy²}{dx}={dy²}{dy}{dy}{dx}=2y{dy}{dx}\ とする. 後は(分母)0に注意して{dy}{dx}を求め,\ さらに接線の方程式を求める. (y-y₀)y₀=2p(x-x₀)→y₀y-{y₀}²=2px-2px₀→これに{y₀}²=4px₀を用いた後整理. y₀=0のとき,\ つまり頂点(x₀,\ y₀)=(0,\ 0)における接線は明らかにx=0である. これが含まれていることにも注意して最終的な答えとする. 様々な解法が考えられるが,\ 図形的な特徴を利用すると簡潔に済む. まず平行線の錯角を考慮すると,\ FPA}が二等辺三角形}であることの証明に帰着する. それには{PF=AF}を示せばよく,\ さらに{PF=PH}を考慮すると{PH=AF}の証明に帰着する. {PとHのx座標から,\ PHの長さがすぐに求まる.} このとき,\ x₀とpの大小関係による場合分けを避けるために絶対値をつけておく. さらに接線の方程式とx軸との交点として{A}の座標を求めると,\ {AF}の長さも求まる. }]$ ${放物線y²=4px上の点(x₀,\ y₀)における接線の方程式}$} dy}{${y₀y=2p(x+x₀)$} $[l} 放物線の接線の公式を使う機会は少ないが,\ 一々求めるのも面倒なので{暗記推奨}である. y²=2p2x\ として,\ {y²\ →\ y₀y,2x\ →\ x+x₀}\ と対応させて覚えるとよい. }]$ パラボラアンテナ・懐中電灯の原理} {∠ FPA=∠ HPA}より,\ 上図において\ ∠ FPA=∠ IPB\ が成立する. よって,\ 放物線を鏡とすると,\ {x軸と平行に入射してきた光は反射後焦点に集まる}ことがわかる. これがパラボラアンテナの原理である.\ 焦点に受信器を設置すると,\ 微弱な電波でも受信できる. 逆に,\ {焦点から発射した光は反射後x軸と平行に進行}する. これが懐中電灯の原理である.\ 焦点に電球を設置すると,\ 光が平行に直進して遠くまで届く.

