先に次を確認することを強く推奨します。
(2)の解答でB(b₁,b₂)を代入した式が「t₁t₂/4+t₂b₂=1」となっていますが、「t₁b₁/4+t₂b₂=1」の誤りですm(_ _)m
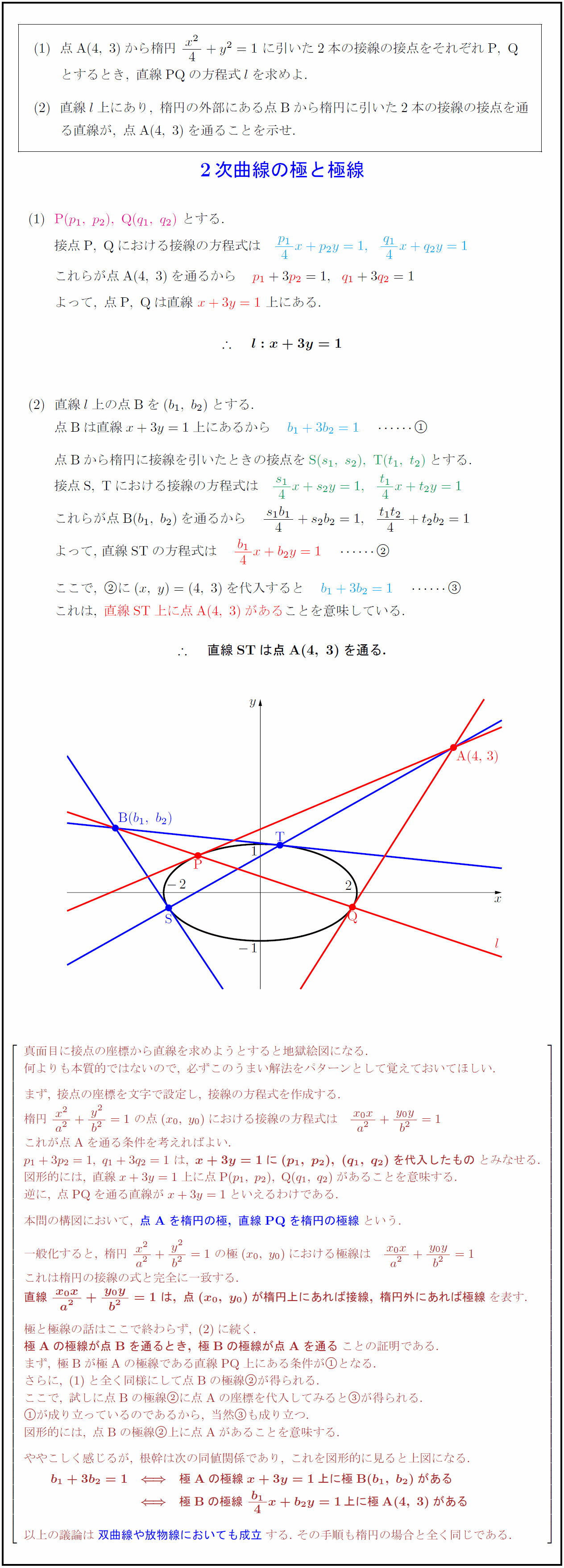
点{A}(4,\ 3)から楕円\ {x²}{4}+y²=1\ に引いた2本の接線の接点をそれぞれ{P,\ Q}$ $とするとき,\ 直線{PQ}の方程式lを求めよ.$ $直線l上にあり,\ 楕円の外部にある点{B}から楕円に引いた2本の接線の接点を通$ $る直線が,\ 点{A}(4,\ 3)を通ることを示せ.$ $接点{P,\ Q}における接線の方程式は {p₁}{4}x+p₂y=1,{q₁}{4}x+q₂y=1}$ 真面目に接点の座標から直線を求めようとすると地獄絵図になる. 何よりも本質的ではないので,\ 必ずこのうまい解法をパターンとして覚えておいてほしい. まず,\ 接点の座標を文字で設定し,\ 接線の方程式を作成する. 楕円\ {x²}{a²}+{y²}{b²}=1\ の点(x₀,\ y₀)における接線の方程式は {x₀x}{a²}+{y₀y}{b²}=1 これが点{A}を通る条件を考えればよい. p₁+3p₂=1,\ q₁+3q₂=1\ は,\ {x+3y=1に(p₁,\ p₂),\ (q₁,\ q₂)を代入したもの}とみなせる. 図形的には,\ 直線x+3y=1上に点{P}(p₁,\ p₂),\ {Q}(q₁,\ q₂)があることを意味する. 逆に,\ 点{PQ}を通る直線がx+3y=1といえるわけである. 本問の構図において,\ {点{A}を楕円の極,\ 直線{PQ}を楕円の極線という. 一般化すると,\ 楕円\ {x²}{a²}+{y²}{b²}=1\ の極(x₀,\ y₀)における極線は {x₀x}{a²}+{y₀y}{b²}=1 これは楕円の接線の式と完全に一致する. {直線\ {x₀x}{a²}+{y₀y}{b²}=1\ は,\ 点(x₀,\ y₀)が楕円上にあれば接線,\ 楕円外にあれば極線}を表す. 極と極線の話はここで終わらず,\ に続く. 極Aの極線が点Bを通るとき,\ 極Bの極線が点Aを通ることの証明である. まず,\ 極{B}が極{A}の極線である直線{PQ}上にある条件がとなる. さらに,\ と全く同様にして点{B}の極線が得られる. ここで,\ 試しに点{B}の極線に点{A}の座標を代入してみるとが得られる. が成り立っているのであるから,\ 当然も成り立つ. 図形的には,\ 点{B}の極線上に点{A}があることを意味する. ややこしく感じるが,\ 根幹は次の同値関係であり,\ これを図形的に見ると上図になる.\ {b₁+3b₂=1極{A}の極線x+3y=1上に極{B}(b₁,\ b₂)がある} b₁+3b₂=1}極{B}の極線\ {b₁}{4}x+b₂y=1上に極{A}(4,\ 3)がある} 以上の議論は{双曲線や放物線においても成立する.\ その手順も楕円の場合と全く同じである.


