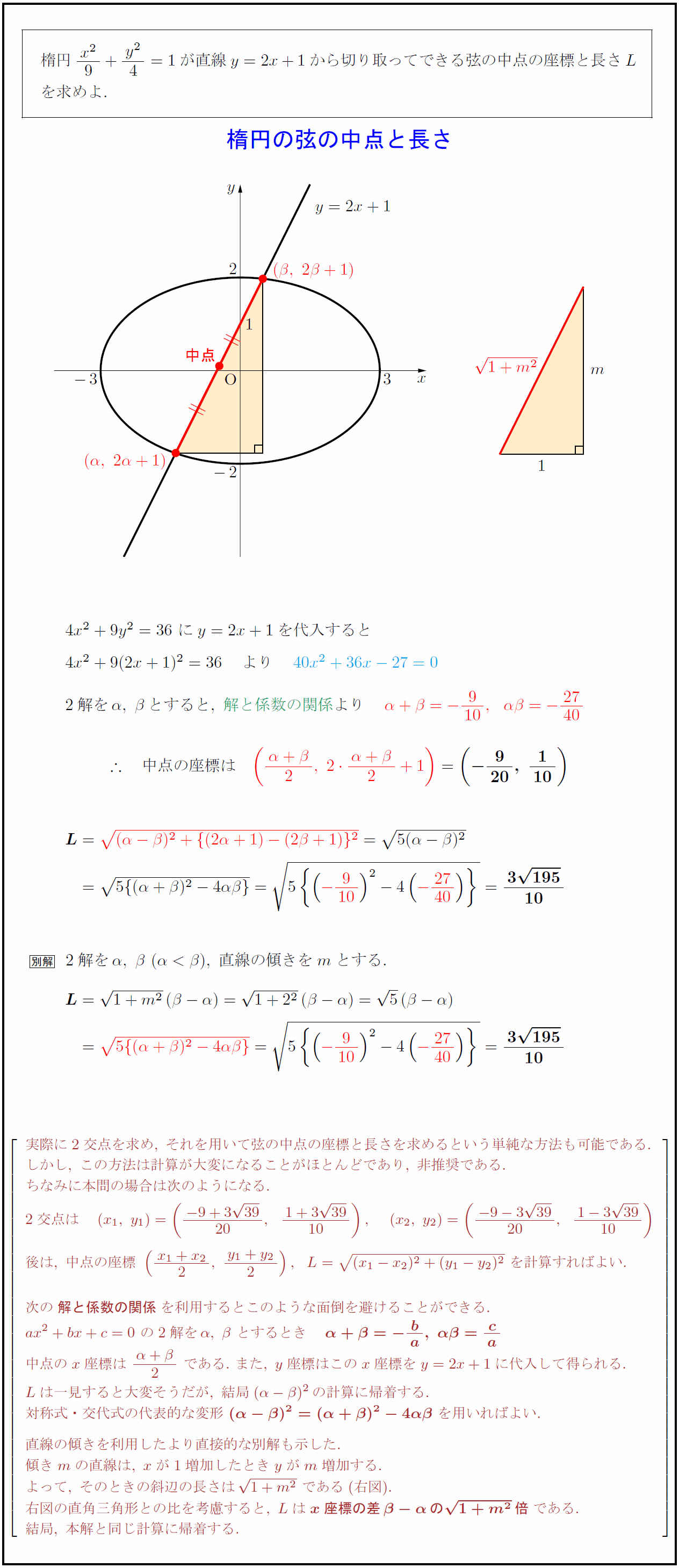
楕円${x²}{9}+{y²}{4}=1$が直線$y=2x+1$から切り取ってできる弦の中点の座標と長さ$L$ $2解をα,\ βとすると,\ 解と係数の関係}より 中点の座標は $2解をα,\ β\ (αβ),\ 直線の傾きをmとする.$ 実際に2交点を求め,\ それを用いて弦の中点の座標と長さを求めるという単純な方法も可能である. しかし,\ この方法は計算が大変になることがほとんどであり,\ 非推奨である. ちなみに本問の場合は次のようになる. 2交点は (x₁,\ y₁)=({-9+3{39{20},{1+3{39{10}), (x₂,\ y₂)=({-9-3{39{20},{1-3{39{10}) 後は,\ 中点の座標\ ({x₁+x₂}{2},\ {y₁+y₂}{2}),L={(x₁-x₂)²+(y₁-y₂)²}\ を計算すればよい. %{({3{39{10})²+({3{39{5})²}={3{195{10} 次の{解と係数の関係}を利用するとこのような面倒を避けることができる. ax²+bx+c=0\ の2解をα,\ β\ とするとき {α+β=- ba,\ αβ= ca} 中点のx座標は\ {α+β}{2}\ である.\ また,\ y座標はこのx座標をy=2x+1に代入して得られる. Lは一見すると大変そうだが,\ 結局(α-β)²の計算に帰着する. 対称式・交代式の代表的な変形\ {(α-β)²=(α+β)²-4αβ}\ を用いればよい. 直線の傾きを利用したより直接的な別解も示した. 傾きmの直線は,\ xが1増加したときyがm増加する. よって,\ そのときの斜辺の長さは{1+m²}\ である(右図). 右図の直角三角形との比を考慮すると,\ Lは{x座標の差β-αの{1+m²}倍}である. 結局,\ 本解と同じ計算に帰着する.

