当ページには大学入学共通テスト(旧センター試験)過去問のネタバレ(問題と解答)がかなり含まれています。
過去問演習を行う前にネタバレを見てしまうと過去問演習の意味合いが半減してしまいます。
受験生は各自適切なタイミングで閲覧してください。
問題を解いた直後に閲覧するとリアリティが増すかも?
2015年センター試験直前、特に浪人生の間にはかつてない緊迫感があった。前年の国語の惨劇を経験していたからである。
しかも、新課程への移行に伴う浪人生への救済措置はわずか1年だけ。もしさらに浪人するとなると、範囲が膨大になった新課程(非ゆとり教育課程)を勉強して受験しなければならなくなる。「何が何でも今年決めなくては」という背水の陣で臨むセンター試験である。
2014年センター試験国語の惨劇と1点の重み
遡ること2年、2013年センター試験では難化した国語によって多くの受験生が壊滅した(2012年平均117.94/200点 → 2013年101.04過去最低)。これを受けて2014年の受験生はタカをくくっていた。
2014年現役生 「去年最高難度だったんだから今年の国語は易化するだろうな。いい年に生まれたわw」
2014年浪人生 「去年は国語でやらかしたが今年こそ志望校合格するぞ!」
2014年出題者 「さらに難化です。」
2014年受験生 「ぎゃああああああああああああ」
平均が5割を切って98.67点(もちろん過去最低)。半端な難易度ではなく、マーク試験なのに約50万人が受験して最高点195点。つまり満点0人。受験生に混じって力試しや調査目的の国語教師もいたはずなのにである。
また、文系の最難関学部である東京大学文科一類の合格者平均が154点(2012年は177点)であったという(河合塾調べ)。
こうなると次のような惨劇が頻発することになる。
2014年医学部受験生 「ああ・・・なんでこんなことに・・・。数学192/200、英語189/200、物理96/100、化学100/100、地理86/100、国語84/200、合計746/900」
センター試験総合9割を要求される東大・京大や国立医学部受験生にとって、1問の配点が8点にもなるセンター国語はまさに鬼門である。たった3問間違えるだけで国語が9割を切ってしまう。そうすると、1問の配点が2~4点である数学・理科・社会で正解した6~12問分の点数が一気にチャラになる。
点数がゴリゴリ減っていく国語の自己採点はまさにトラウマもの。国語の難化は他科目における努力を無に帰すだけの破壊力を秘めているのである。
普通の学生は知らないことだが、国立医学部医学科の合格に必要な学力は他学部学科とは別次元である。
富山大学のベネッセ・駿台リサーチの結果(900点満点、ボーダーライン;合格率60%)を例としてあげておく。センター試験の難易度に関わらず、点を取る人は点を取る。このような最上位層の争いにおいて、センター試験で失敗してしまうと2次記述試験で挽回するのは容易ではない。
| 富山大学 | 工学部 | 医学部看護科 | 薬学部薬学科 | 医学部医学科 |
|---|---|---|---|---|
| 2014年 | 555 | 565 | 725 | 755 |
近年、医学・薬学系の学部を志望する学生は増えてきているが、多くは医学部受験の厳しさを知らずに「ただ何となく」というのが現状である。高い学力と他学部の数倍の学費(私立ともなると数千万)が必要で、その他「全科目必修で1つでも落とせば留年」「1回の定期試験の勉強量が受験勉強と同じくらい」「実際の人間の遺体での解剖実習が必修」などとも聞く。「医学部合格に何が必要なのか」「合格後どうなるのか」などについて全く調べていない医学部志望の学生は本気の程が疑われる。もっとも、遅かれ速かれ嫌でも現実を思い知ることになる。
また、大学受験における1点の重みが東大受験から見えてくる。
東大では、まずセンター試験900点満点を110点に圧縮する(約1/8)。これは割り切れず、小数第5位を四捨五入した小数第4位までが各受験生のセンター試験の持ち点となる。これに2次記述試験(440点満点)を足した合計550点満点で合否が判定される。
「1/8に圧縮されるのならセンターの点数なんてあまり関係ないんじゃん」と思えるが、そうではない。
東大理科一類の場合は約2500人が受験し、合格枠は約1000人。これは2500人が一斉に100m競争をするようなもので、合格ライン付近では想像を絶する競り合いをしていると思われる。
百聞は一見にしかず、このことを示す1枚の画像がある。合格最低点が333.9111点であった2012年の東京大学理科一類受験生の成績開示結果である(拾いモノ)。なお、満点は国語80点、外国語120点、数学120点、物理60点、化学60点(計440点)である。
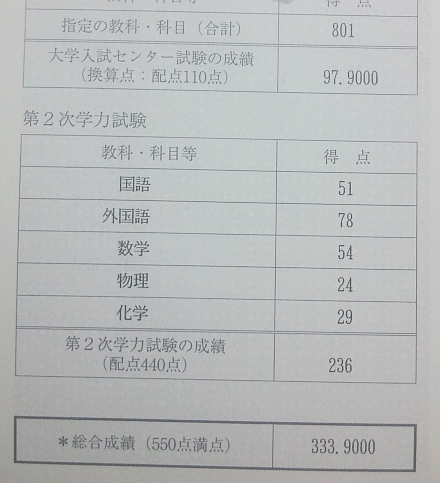
届かなかった・・・後0.0111点。何点差であろうが敗者は敗者。周囲の評価は100点差で落ちた人と変わらない。「センターであと1点取っていれば合計334.0222だったのに・・・」「1日もう5分長く勉強していれば・・・」などというタラレバがむなしく響く。おおよそ同等の能力をもった受験生が非常に限られた枠を争うため、得点が1/8に圧縮されるとしてもセンター試験の1点が最後の最後に重くのしかかってくるのである。
僅差で競り負けたのは「運」がなかったからなのか。それとも「実力」がなかったからなのか。東大がどうかは不明だが、「もう一度試験をやり直すと合格者の下位5割が入れ替わる」とも言われる大学受験の隠れた現実である。
ギリギリ落ちる受験生がいるならば、当然ギリギリ合格する受験生もいる。同じ2012年、1年間の浪人の末、東大文科三類にギリギリ合格した地下アイドルがいた。2016年になって彼女の書籍が発売された。
著者プロフィール
桜雪(さくら・ゆき)
アイドルグループ・仮面女子/アリス十番所属。1992年生まれ。三重県出身。東京学芸大学附属高校を経て、東京大学文学部卒業(心理学専修)。高校3年生の夏、アリスプロジェクトに所属し、受験生アイドルとしてブログ「桜雪の東大一直線娘」(現・「桜雪の東大のすすめ」)を開設。1日10万PVを突破し、アメブロ受験カテゴリーで1位を獲得するなど一躍人気ブロガーに。現役時代はE判定のまま東大受験に失敗するも、1年で学力を大幅アップさせ東大文科三類に合格。在学中は現役東大生アイドル、現在は東大出身アイドルとしてメディア出演多数。目標はエンターテインメントで国際貢献すること。
実は、現役時代にも活用した東大の開示請求を、このときも出したんです。
すると、私はボーダーラインとの差が1点未満で、究極の崖っぷち合格だと言うことがわかりました。
つまり、1点でも落とせば不合格。センター試験でつけたアドバンテージで、ギリギリ生き残った感じです。
できたという手応えが気のせいだったのか、テストが簡単な年で厳しめに採点されたのかはわかりませんが、見た時は冷や汗をかきました。
1点差でも、合格は合格です。そして、東大アイドル・桜雪の活動も本格的にスタートしました。
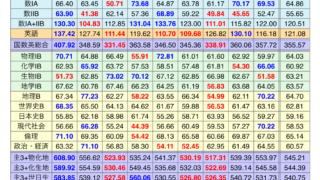
彼女のセンター試験の得点は、英語(筆記)195点、英語(リス)42点、数学1A98点、数学2B88点、国語184点、生物88点、世界史88点、地理85点、合計826点であった。
河合塾によると2012年文科三類の合格者平均は814点であったそうなので、センター試験でのリードが合格につながったといえる。なお、センター利用で早稲田大学法学部政治経済学科、法学部法学科、国際教養学部、明治大学法学部特待合格(学費無料)。
彼女は2016年に大学を卒業後、10月に小池百合子東京都知事が立ち上げた政治塾「希望の塾」に第1期生として入塾、2019年3月には仮面女子を卒業して本名の橋本侑樹(ゆき)で4月に東京都渋谷区議会議員選挙に初当選した。
2015年センター試験
センター試験の重要さがわかったところで大きく横道にそれた話を本道に戻し、2015年のセンター試験を時間を追って見ていく。
1日目 国語直前
2015年受験生 「さすがに今年は易化するだろ・・・でも2年連続難化したし、二度あることは三度あるのか???万が一、去年以上の難度だったら・・・(不安)」
自身の受験が完了してダークサイドに墜ちた高みの見物中の大学生 「難化しろ難化しろ、受験生壊滅しろおおおおおおお(期待)」
1日目 国語終了後
受験生Twitter 「Twitter出たwwwww」
多くの受験生の不安は杞憂に終わった。最近の若者にはとっついやすいTwitterにおけるクソリプ、パクツイを題材にした評論『未知との遭遇』が出題されたりと、全体的に大きく易化した。点数が安定しにくい国語が易化したことで安心感が広まっていた。
浪人生 「今年はいけるぞ(`・ω・´)」
高みの見物中の大学生 「ちっ、つまらん」
ちなみに、入試での使用において筆者に事前連絡はないらしい。情報流出を防ぐ観点に立てば当然だろう。筆者も知り合いから聞いてセンター試験で出題されたことを知ったようである。
筆者Twitter 「どんな設問だったんだろ。なんだか申し訳ないですね。そもそも俺が正解できるのかという、、」
このツイートをみて数年前話題になった某大学の入試問題が思い出された。
某大学 「筆者が『クルマ』と『自動車』を使い分けた理由を答えよ。」
筆者Twitter 「ごめん!筆者、何も考えてなかった!わははは」
2日目 数学IA直前
受験生 「2010年や2013年のような難問は出ませんように・・・」「平年のレベルでお願いします」「いつもⅡBは難しいからIAで稼がないと」
高みの見物中の大学生 「IA難化しろおおおおおおお」
2日目 数学IA終了後
受験生 「簡単だったw」「出題者は受験生なめすぎw」
高みの見物中の大学生 「ちっ、つまらん」
2日目 数学ⅡB直前
受験生 「IAが簡単な年はⅡBが難しいのが相場だ。心してかからないと」
高みの見物中の大学生 「ⅡB難化しろおおおおおおお」
2日目 数学ⅡB終了後
受験生 「難しすぎ」「国立オワタ・・・」「時間足りねえええ」「こんな問題出すとか出題者頭おかしい」
高みの見物中の大学生 「(゚∀゚)アッヒャッヒャッヒャッヒャ」
拙者 「ⅡB後の反応は毎年恒例だな。今年の問題は・・・どれどれ・・・。特別難しい問題は見あたらないな。うん、なんだかんだで例年通りだろう。」
拙者 「(数時間後)あれ?何かいつもと違う不穏な空気が・・・・・・」
センター試験2日後 各予備校が集計速報発表
衝撃的なツイートが拡散され、伝説の入試問題の仲間入りが決定付けられる。
「数ⅡBの平均27点wwwww」
ただ、この情報は半分正しく半分間違いである。真相は次の画像にある。
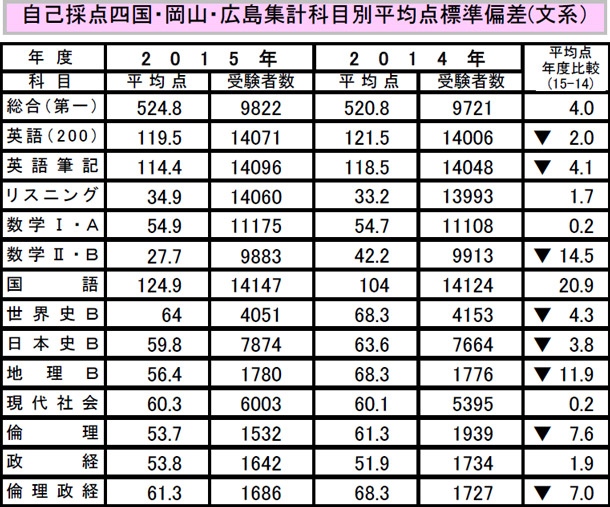
この高松高等予備校(香川県)が集計した地方の文系学生の平均が西日本放送テレビ(RNC)で放送されたことにより、一気にTwitterで拡散されたのである。
そして、有名予備校の集計速報が出揃う。その平均の低さに驚いた教師や数学が得意な理系学生も多かったであろう。
「えっ、なんでこの問題でこんな低くなるの???」
実際、某予備校の講評は3段階の進化を見せた。
「手が止まるような問題がないので、去年より易化」
↓
「無理がない内容だが、分量が多く受験生が取り組みにくい問題もあるので、昨年並み」
↓
「無理がない内容だが、分量が多く受験生が取り組みにくい問題もあるので、去年より難化」
何故これほどにまで平均が低くなったのか、周囲やネットの反応からその理由がわかってきた。出題された問題と共に見ていくとしよう。
第1問 三角関数

受験生 「いやあああああああああ、7倍角なんてそんなの覚えてるわけないよ。ダメだ・・・どうしようもない。この問題は捨てよう。」
きちんとセンター対策した受験生 「なんだ、加法定理の逆か。過去問でも何度か見かけたな(←ココ重要)。」
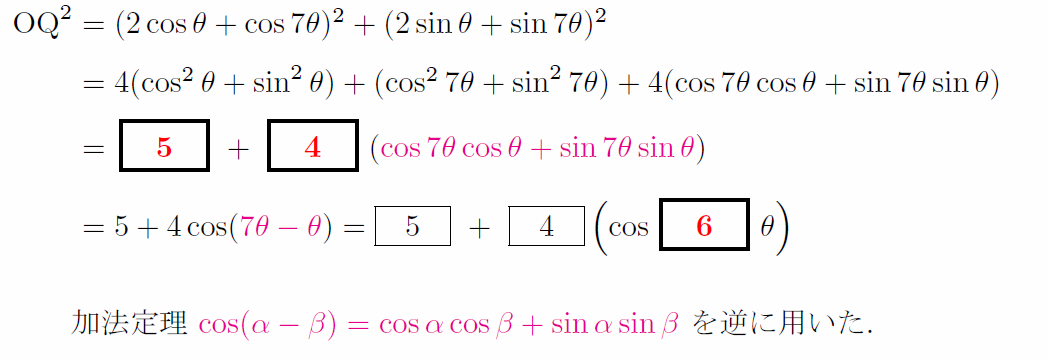
中途半端に能力のある受験生 「積和の公式しか思い浮かばない。たぶん正攻法ではないけどそんなこと言ってる場合じゃねえ」
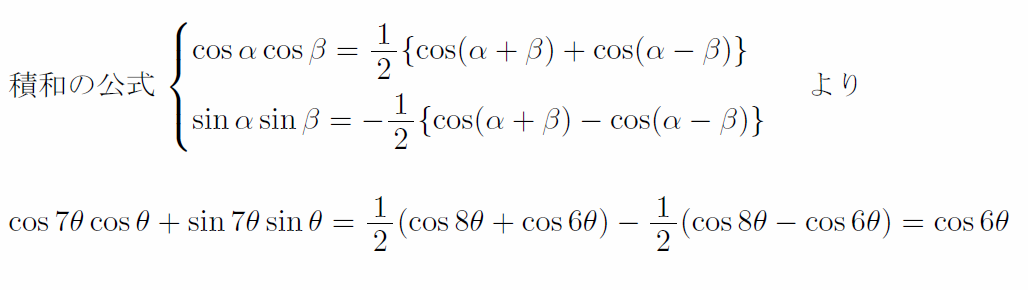
このように本問への対応は様々だったわけだが・・・・・・
教師&数学が得意な人 「7倍角って・・・その発想はなかった」
7θを見て「7倍角だ」と思う人は、100θを見ても「100倍角だ」と思うのだろうか。あたかも2倍角の公式や3倍角の公式の一種であるかのように。そんなはずはないだろう。
本問は加法定理の逆を適用するべきであり、その変形においては7という数字に本質的な意味合いは全くない。7だろうが8だろうが100だろうが同じである。「7倍角」などという言葉を持ち出す時点で、それまでに的外れな学習を積んでいたであろうことが露呈してしまっているのである。
ただし、通常の受験勉強において加法定理の逆を使う機会はかなり少なく、多くの受験生は一度も経験していないと思われる。加えて、数Ⅲで使う理系ならまだしも文系は積和の公式を使う発想に至るはずもなく、見事に壊滅したわけである。
ところで、本問は穴埋め部分の多くが1桁の整数である。このような場合、わからなくても適当な数字を入れておけば十分当たる可能性があるにもかかわらず、糞真面目に白紙にしたままで終わる受験生が多い。他科目では全部埋めるのに何故か数学だけ埋めないのである。「数学は他科目のように単純な4択、5択じゃないからどうせ当たらない」とでも思っているのだろうか。
よくよく考えてみると、πの分母の「カ」はθの範囲から4,5,6,7,8しかありえず、さらに普通に考えてπの分母が5や7になる可能性はきわめて低いから4,6,8の実質3択、根号の中の「キ」は0,1,4,8,9はありえないから2,3,5,6,7の5択だ~よ。さらにさらに裏技的に・・・・・・おっと、ここではこれくらいにしておこう。後は最後のリンクから裏技のページへ。
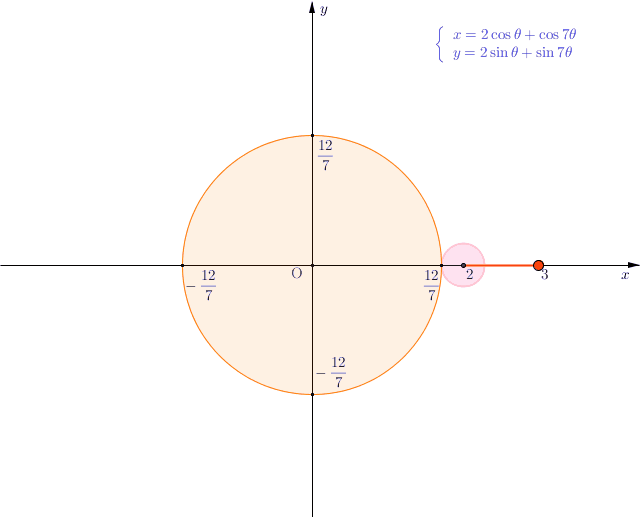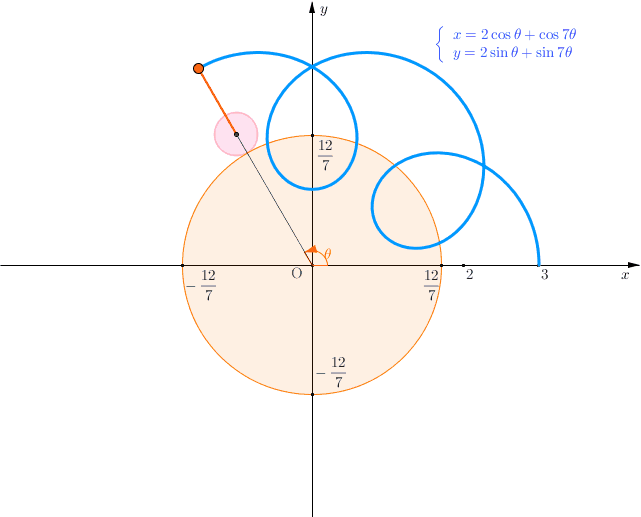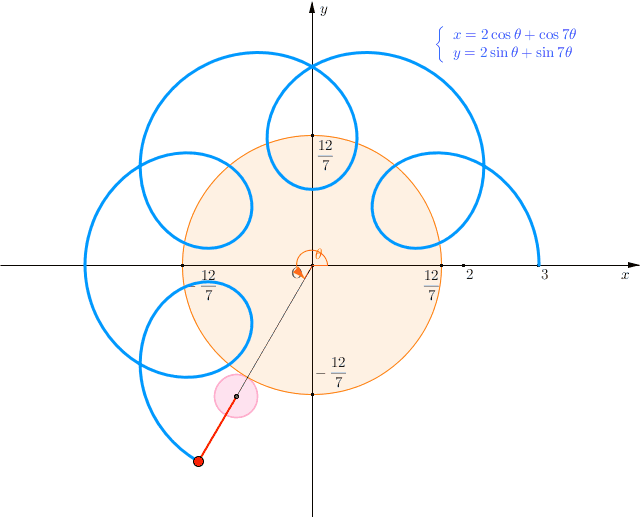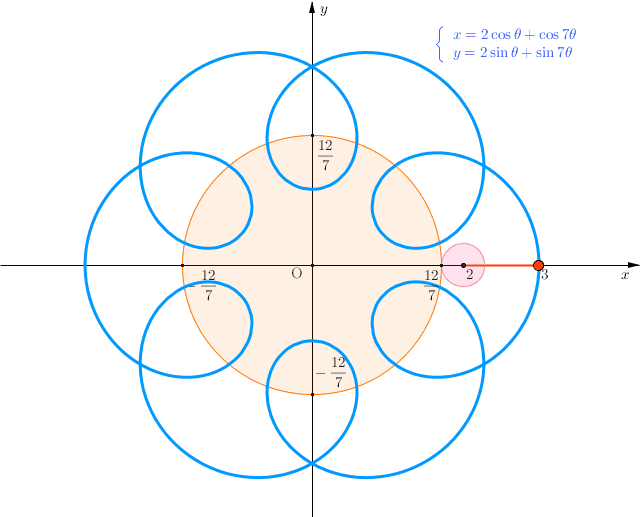
また、本問は図形的意味がおもしろい。
点Qの描く軌跡が図の青色の曲線(お花みたい)であり、θの範囲内が赤色の部分である。OQ2が最大、つまり原点と点Qの距離が最大になるのはθ=π/4のときである。
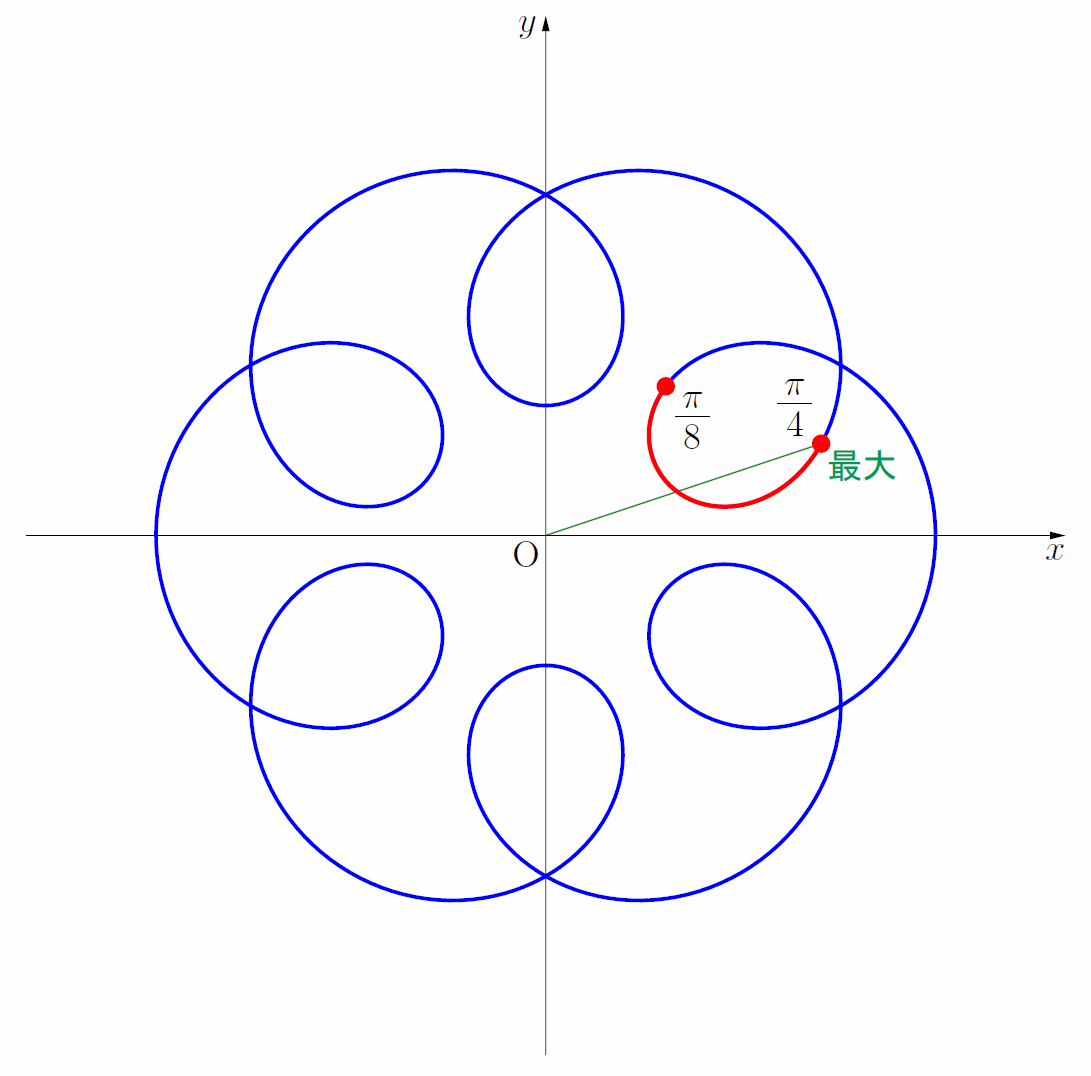
実は、この曲線は外トロコイド曲線(定円に外接しながら動円が回るときの定点の軌跡)である。
本問の曲線は、半径12/7の定円に外接する半径2/7の動円が回るとき、動円の中心から1の距離にある定点が描く点の軌跡である。数Ⅲでハイポサイクロイドやエピサイクロイドに関する学習をした理系ならば多少とっつきやすいだろう。
トロコイドといえば、子供の頃にスピログラフという玩具で遊んだことが思い出される。
スピログラフは、内トロコイド曲線(定円に内接しながら動円が回るときの定点の軌跡)を描くことができる。このような玩具を子供に与え、それとなく数学的背景があると匂わせておくことが教育上重要である。
なお、途中でずれたりしてきれいに描くのは思いの外難しい・・・・・・

第1問 指数関数
三角関数をあきらめた受験生が次に取りかかったのが指数関数の問題である。
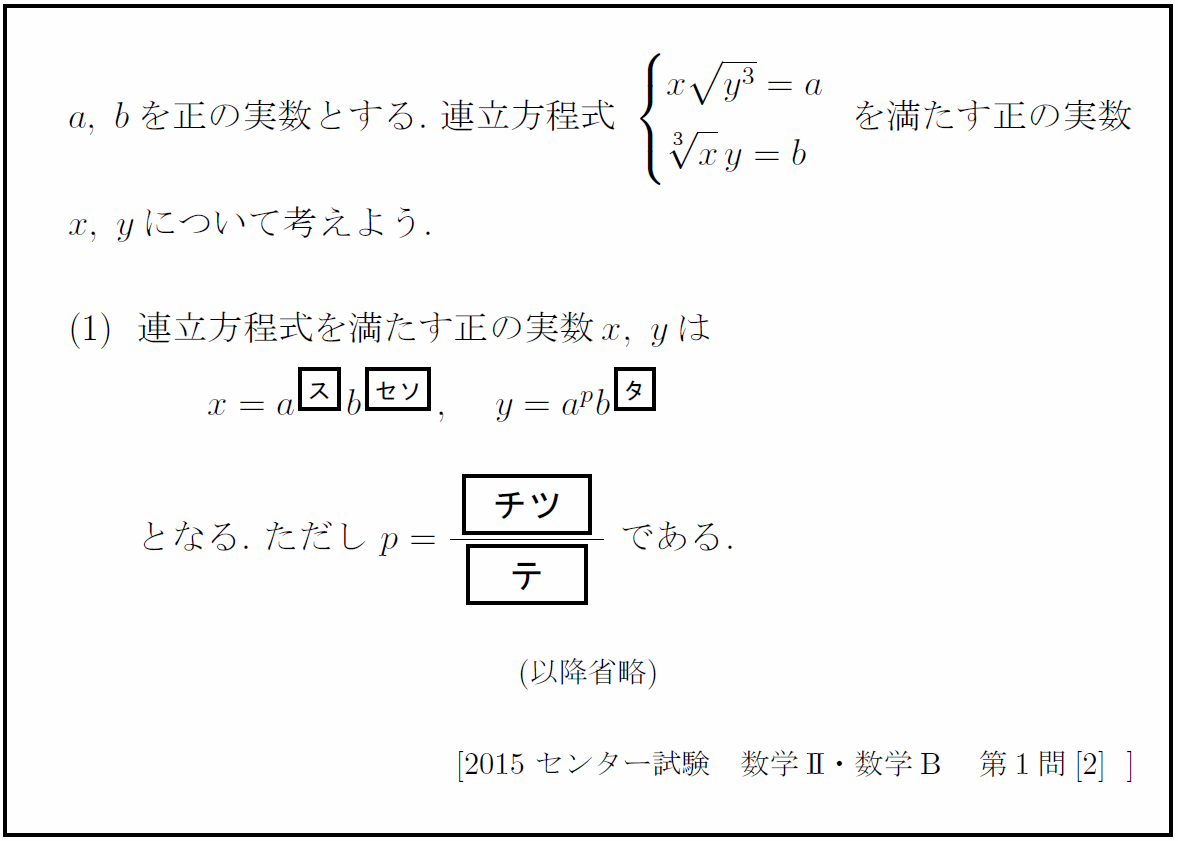
受験生 「いやあああああああああ、何この連立方程式。どうやって解けばいいの。足しても引いてもどうにもならないよ。」
数学が得意な受験生 「なんだ、ただの2文字の連立方程式か。一文字消去っと。」
「連立方程式の大原則は一文字消去」を認識できている学生にとっては容易な問題で、多少ゴリ押しになっても確実に解くことができる。つまり、一方をx=かy=にしてもう一方に代入すればよいのである。
しかし、認識できていない学生は驚くほど多い。その認知度は並以下の学生では壊滅的、さらに文系になると難関大学受験生であってもかなり怪しい。
認知度の低さは、おそらく中学生の時に学習する2元連立1次方程式の加減法に意味も分からず慣れすぎているせいだろう。
連立方程式は「足したり引いたりすると解ける」などという大きな誤解が蔓延しているのである。その結果、次のようなことを平気でやる学生があまりにも多い。
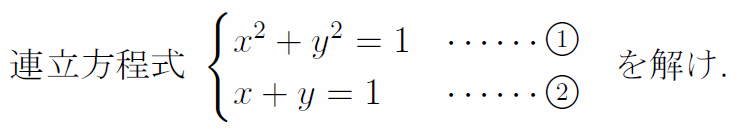
学生 「ラッキー♪ 右辺の1が簡単に消去できる(゚∀゚)」
教師 「お、おいおい(・∀・;)」
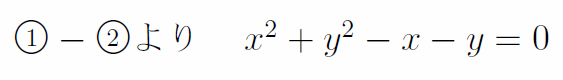
学生 「あれ?なんか余計に複雑になっちゃった。あっ、①を使えば簡単にできそう(゚∀゚)」

学生 「(´;ω;`)ウッ」
教師 「・・・・・・・・・・・・」
もちろん、1文字yを消去するために、②をy=ーx+1として①に代入してxのみの式にすれば容易に解ける。このように、「連立方程式を解く」という単純計算においても、最低限の理解が伴っていなければ応用が利かないのである。
第2問 微分積分
連立方程式の原則を知らずに指数関数に門前払いされた受験生は、「微積なら計算するだけなのでできるはずだ」などと考えてこの問題に着手することになる。
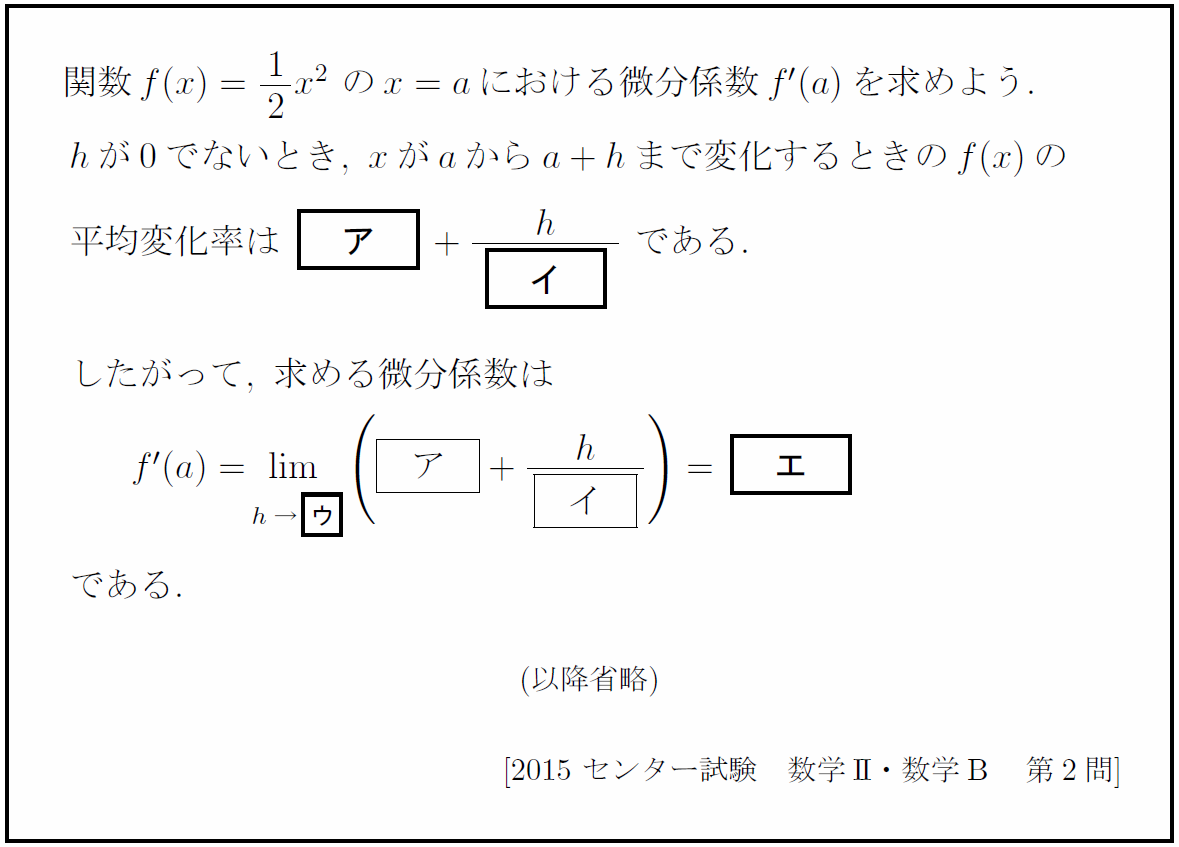
理系 「なんだ、微分係数の定義か。数Ⅱの範囲で問われるとは珍しいな。」
文系 「いやあああああああああ、平均変化率って何それ。しかもlimって何この記号。極限?数Ⅲの範囲じゃないの?無理だああああ」
微分係数の定義自体は数Ⅱの学習内容であるが、数Ⅲで頻出する理系とは異なり、文系はその後問われることがほとんどないためにすぐに忘れ去る。その結果、このような超基本問題に対しても全く対応ができなくなるのである。
また、文系の微分積分に対するそもそもの認識にも問題がある。学生だけの問題ではなく、教育システムの問題でもある。
文系 「微分?ああ、なんかよくわからないけど接線の傾きが求まるんだって」
文系 「積分?ああ、なんかよくわからないけど微分と逆の関係にあって定積分すると面積が求まるんだって」
本来は、最低限の理解が伴っていれば微分係数についてもそうそう忘れないはずなのである。
さらに、数学の試験を受ける際の学生の姿勢にも問題がある。というのも、(1)が解けないというだけで大問をまるごと捨てる学生が結構いるのである。(1)が解けなくても(2)が解けるかもしれないのに。
本問についても微分係数以外の部分は普通に解ける可能性があったにもかかわらず、見もしないで早々に捨てているのには言葉を失うばかりである。
第3問 数列
「三角関数も指数関数も微積もわからない・・・数列なら・・・数列なら・・・」
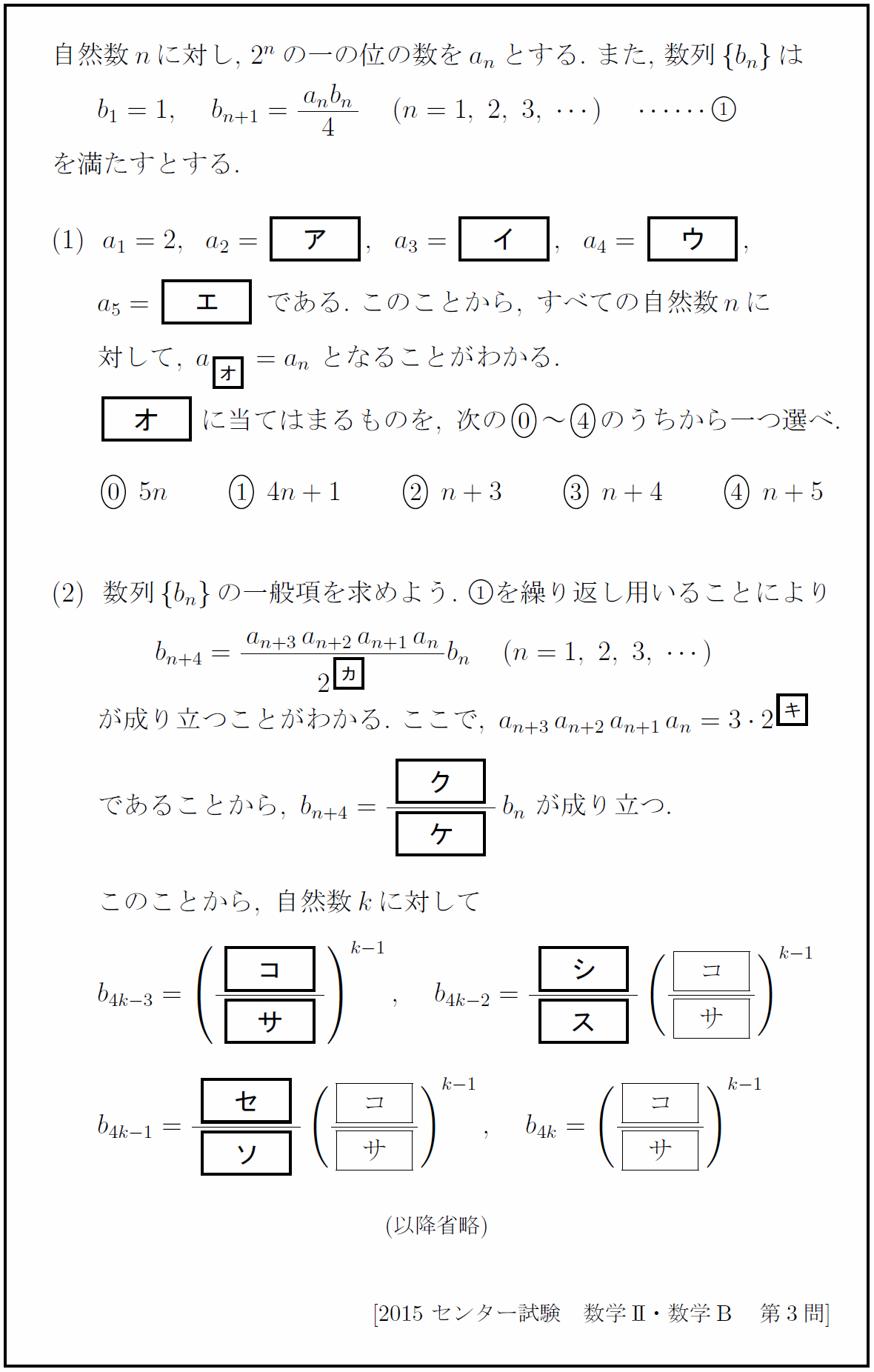
受験生 「もういやあああああああああああ、何なのこの漸化式。こんなパターン見たことないよ。どうすればいいの。そもそも問題の意味がわかんない。」
周期数列に絡めた漸化式の問題だが、これは中々厄介である。いわゆるパターンではないため、センター用のパターン問題演習しかしてきていない文系や並以下の受験生には以降の対応が困難なのである。一方で、2次記述試験用の演習を繰り返してきた学生にとってはさほど手こずる問題ではない。
また、裏技を習得していた場合、以降が一気に超サービス問題と化す。
実際、裏技を習得済みの人には次のように見える。
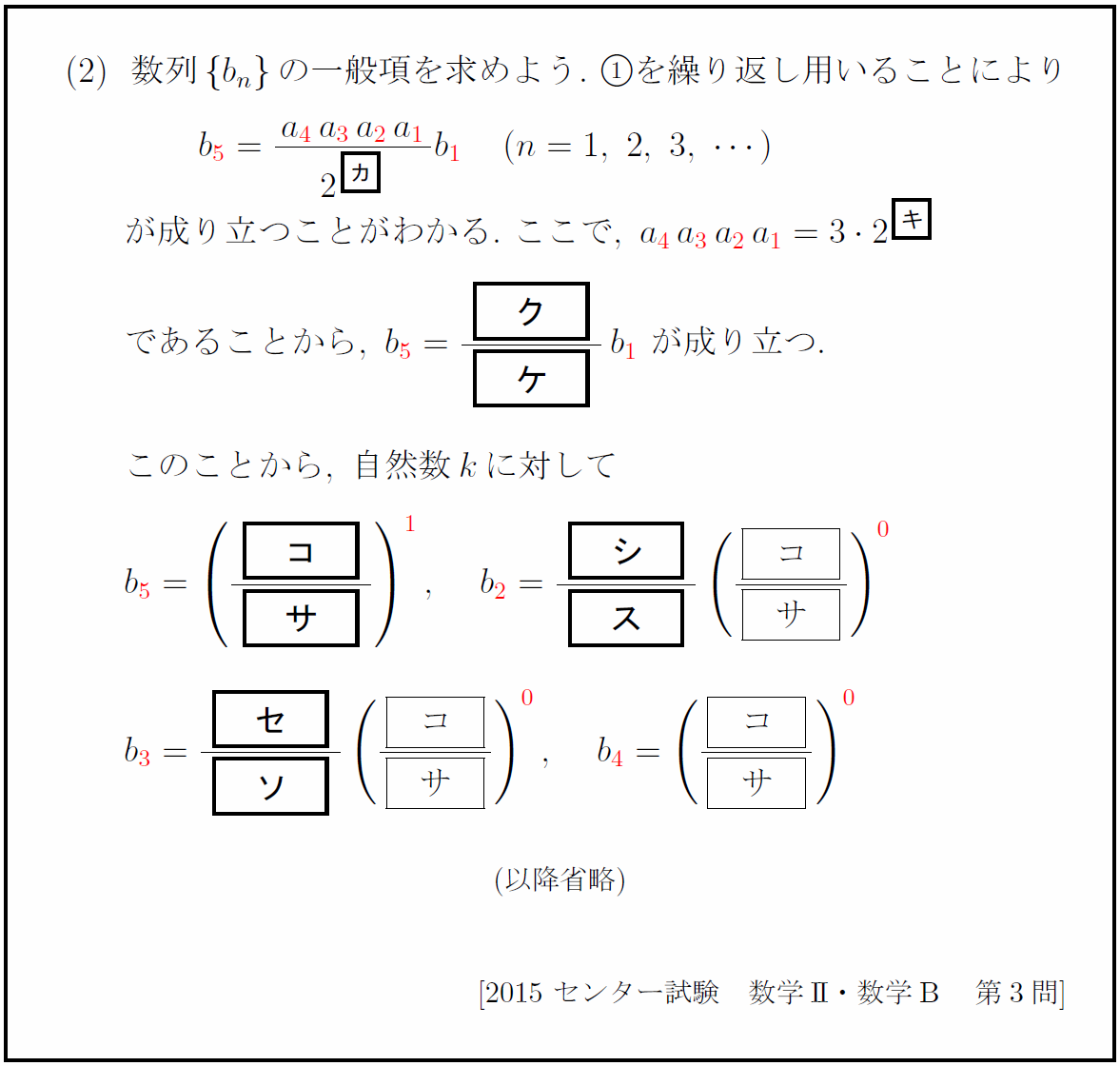
穴埋め式試験では文字のまま考える必要はなく、特殊な場合だけ考えればよい。そこで、n=1、k=1(一部k=2)とするとこのように見えるわけである。後は次のように具体的に計算してあてはめるだけで容易に穴埋めできる。
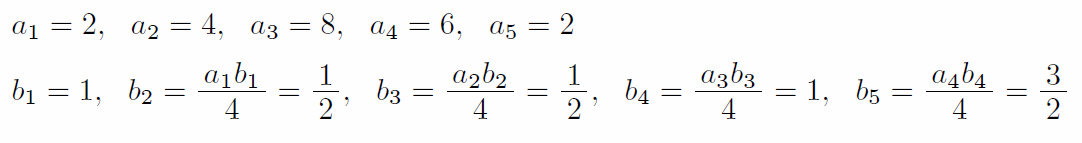
これが「必要条件から攻める」というセンター数学最凶の裏技である。
数列は元々この裏技が使える可能性が高い分野であり毎年多少は使えるのだが、2015年は半分以上がほぼ裏技だけで埋めることができるという近年まれに見る裏技の当たり年であった。
第4問 ベクトル
すでにパニック状態の受験生は最後の第4問ベクトルに着手する。しかし・・・・・・
受験生 「ベクトル基本問題なのに時間があああああ。ベクトルから先にやるべきだった・・・。」
試験終了間近でベクトルの簡単さに気付いても時既に遅し。普段から意識的・戦略的に時間配分する訓練をしていなかった受験生に訪れる必然である。
制限時間が非常に厳しいセンター試験では、「早いうちにすべての問題に目を通し、簡単な問題から先に解く」のが超大原則なのである。
最後に
センター数学が1997年に現在のIAⅡBの形式になって以来、数ⅡBの平均点が最も低かったのは1998年に記録された41.38点であった。
この年の平均点が低かった1つの要因は次の問題にある。

受験生 「cos型の合成だと・・・・・・」
sin型の合成は基本事項だが、cos型の合成は存在すら知らない学生がほとんどである。
「合成が加法定理の逆であることを認識しており、その根幹に立ち戻って処理する」「無理矢理sinからcosに変換する」のどちらかができなければ解答できないという意味で難問である。
過去のセンター試験数ⅡBでは、理系の難関大学受験生ですら固まるような難問が出題され、受験生を壊滅させてきた。2004年ベクトル、2009年ベクトル、2012年三角関数などである。これらの年ですら平均は50点前後で、1998年の最低記録41.38点には遠く及ばなかった。41.38点はまさに不滅の記録だったのだ。
しかし、2015年の最終的な平均点は39.31点、ついに1998年から17年間守られてきた不滅の最低記録は更新された。特別に難問と言えるものがあったわけではなく、言うなれば見せかけだけの問題ばかりであったにもかかわらず、まさかの伝説誕生となってしまったのである。
このような惨劇が起こる背景には、センター試験の功と罪がある。
言うまでもなく、ほぼすべての大学受験生がセンター試験を受ける。すべての大学受験生に共通する試験で受験できるのは非常に公平なシステムである。
しかし、全受験生が受けるということは、学校や塾ではどうしてもセンター試験を想定した授業や演習が中心になるということである。センター試験の過去問を確認し、出題頻度が高い問題を中心に演習を行うことになる。
その結果恐ろしいことが起こる。
過去にセンター試験で問われたことがない内容やポイントについては学校や塾でも非常に軽視され、場合によってはまともに学習しない。
その代表例は「数学的帰納法」であろう。2013年になるまでセンター試験で数学的帰納法が出題されたことはなかった。「数学的帰納法はセンターには出ないから勉強しなくてもいいよ♥もっと優先すべきこといっぱいあるよ」などと言っていた教師が全国に多数いたであろうことは容易に推測できる。
こうして数学的帰納法をまともに使いこなせない大学生が長年にわたって大量に生産されてきたのである。その影響を最も受けるのは大学の先生達である。本来は高校生の内にマスターしておくべき数学的帰納法を使えない大学生を前にして嘆かわしく感じていたであろう。
センター数学の出題者は大学教授である。数学的帰納法を使えない大学生を直接見てきた大学教授が「よし、センター試験で数学的帰納法を出題してやろう」と考えるのも当然である。
センター数学は、大学から高校生や高校教師へのメッセージとしての役割をもつ。一度でも出題があればそのインパクトはとてつもなく大きい。2013年以降、受験生は数学的帰納法もきちんと学習せざるを得なくなった。
数学的帰納法のように対策が薄い部分が突然出題されると、センター対策やセンターの過去問演習しかしてこなかった多くの受験生はなす術もなく壊滅する。大問の最後のほうで問われた場合は点数に大きく影響しないのだが、大問の最初のほうで問われると大量失点につながる。
2015年はベクトル以外のすべての大問で受験生にとって盲点となるポイントが問われた。加法定理の逆、積商タイプの連立方程式、微分係数の定義、パターンではない漸化式である。
いずれも出題例がないか、あってもごくまれなものである。その上、すべてのポイントが大問の序盤で問われた。その序盤の難所を乗り越えることができない多くの受験生が各大問での大量失点を余儀なくされ、惨劇となったわけである。
センター試験の裏技はこちら(当サイト)。

センター試験の平均点推移はこちら(当サイト)。
この2015年のセンター試験を受けていた元アイドルの書籍が2016年に発売されたので記事にしました。