2003年 東京大学 / 大阪大学　円周率を３にしようとするゆとり教育への警告？

ゆとり教育

2003年、高校新1年生から新課程が始まろうとしていた。

いわゆる「ゆとり教育課程」である。

ゆとり教育とは、受験戦争や落ちこぼれ対策として学習時間と内容を減らしてゆとりある学校生活の中で思考力を鍛えようとする学習方針のことであり、従来の知識暗記重視の詰め込み教育の対極に位置付けされる。

実は、広い意味でのゆとり教育はすでに1980年代から始まっていた。

第2次世界大戦後のスプートニク・ショック(ソ連が1957年に人類初の人工衛星の打ち上げに成功した際のアメリカを含む西側諸国が受けた衝撃)や高度経済成長期には正義とされた詰め込み教育も、徐々に世論の反発が強くなってきていたのである。

学力の低下や学力格差の拡大を危惧する声もあったが、ゆとりは加速し続け、2003年を迎えることになった。

	1961年-	1971年-	1980年-	1992年-	2002年-
小学校(45分)	5821	6135	5785	5785	5367
中学校(50分)	3360	3535	3150	3150	2940

つまり、2003年からの新課程(小中は2002年から)は、言うなれば「超ゆとり教育課程」である。

2003年東京大学の入試問題

超ゆとり教育課程に対してメディアや受験産業が象徴的に取り上げ、一般的にも大きな話題になったのが、小学算数において「円周率を３にする」という話である。

これに対し、円周率を3とすると円周の長さが正六角形の周の長さと一致してしまうではないかなどと問題視する声が多かった。

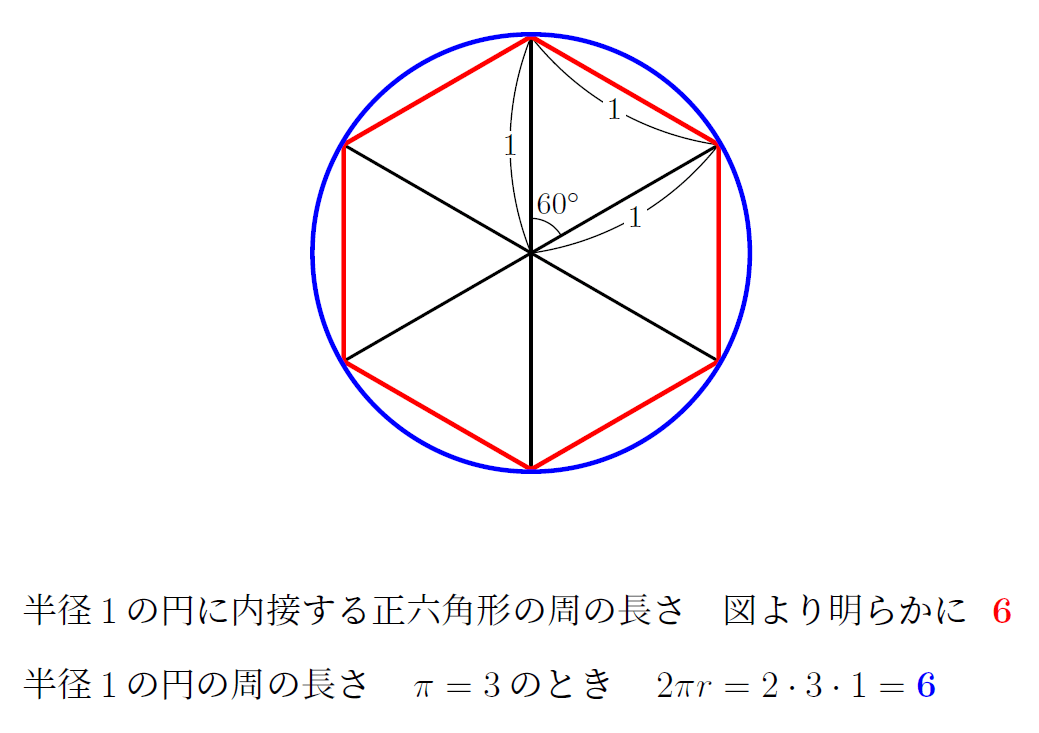
ネットでは「π＝3とすると『おっぱい＝おっさん』になってしまうじゃねぇかよおおぉお、いやだあああぁああ」といったネタも見られた(笑)。

こんな時期に、東京大学が強烈なメッセージ性を感じる問題を出してきた。

問題の意味だけならば小学生でも理解できるシンプルさが秀逸である。

メディアは、「東大がゆとり教育を否定した」などとセンセーショナルに取り上げた。

おそらく、もっとも有名な大学入試問題になっただろう。

天下の東大が出題したからこそ注目されたのであって、他の大学が出しても話題にはなるまい。

有名受験漫画ドラゴン桜(第10巻)の中でも東大を象徴する問題として取り上げられている。

以下に解答を示す。

上にあるように正六角形ではπ>3という非常にアバウトな結果しか得られないので、より多くの頂点をもつ正多角形を持ち出すことになる。

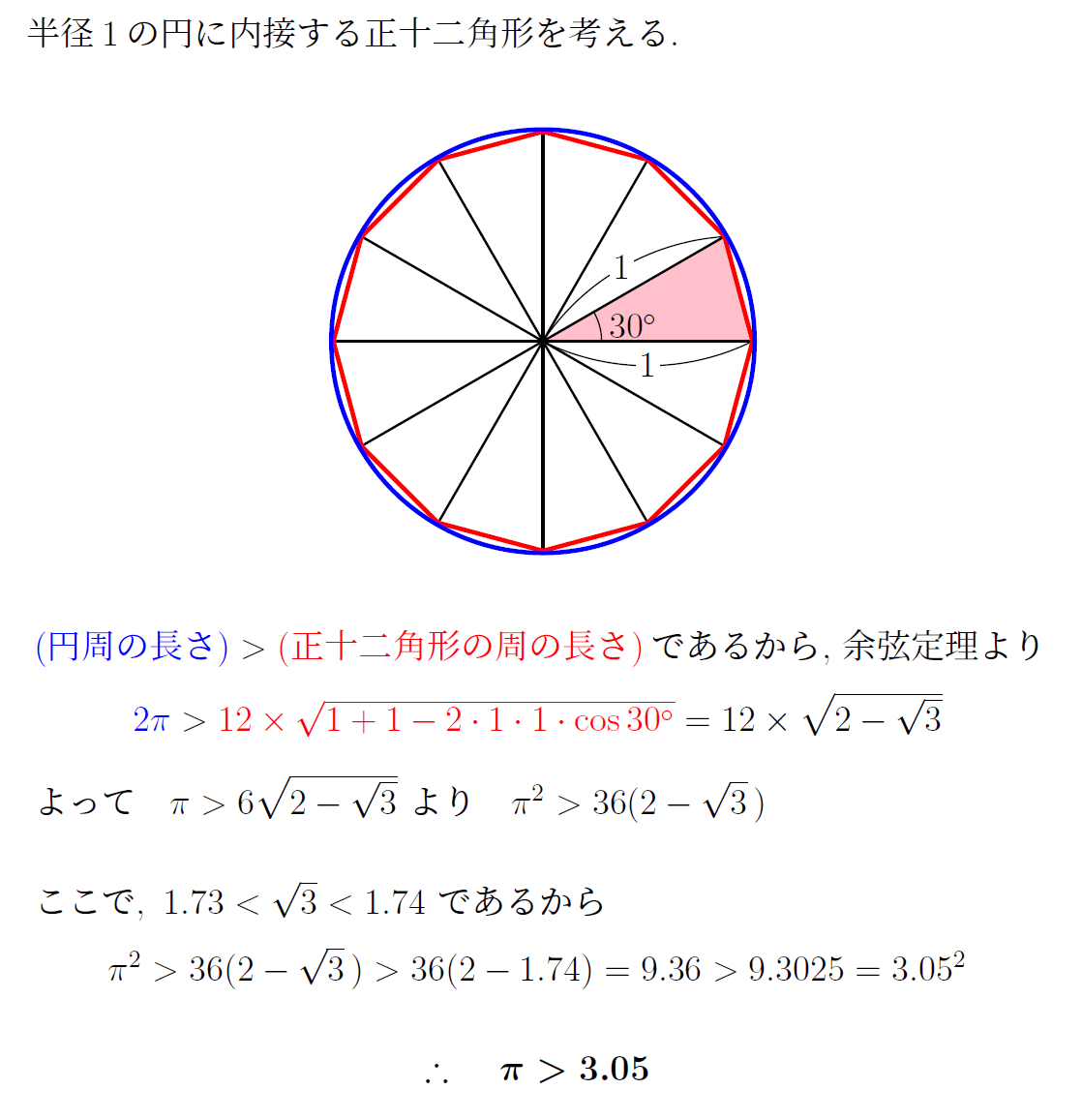
当然ほとんどの受験生が円に内接する多角形の周長との比較で証明していたが、面積で比較していた人が1％ほどいたという。

解答を見て理解できない東大受験生はいないだろうが、あまり出来は良くなかったらしい。簡単といえば簡単な問題だが、東大入試は時間制限が厳しいため、正何角形で考えるかや周長と面積のどちらで比較するかといった最初の方針を誤ると完答が難しくなる。

なお、1.732<√3<1.733を用いると、3.1よりも大きいことまでを示すことができる。

2003年大阪大学の入試問題

同じ2003年、大阪大学の後期試験で以下のような問題も出題された。

円周率は3なのか、あるいは3.14なのか。

いや、どちらでもない。

円周率は小数以下が無限に続く無理数なのだ！

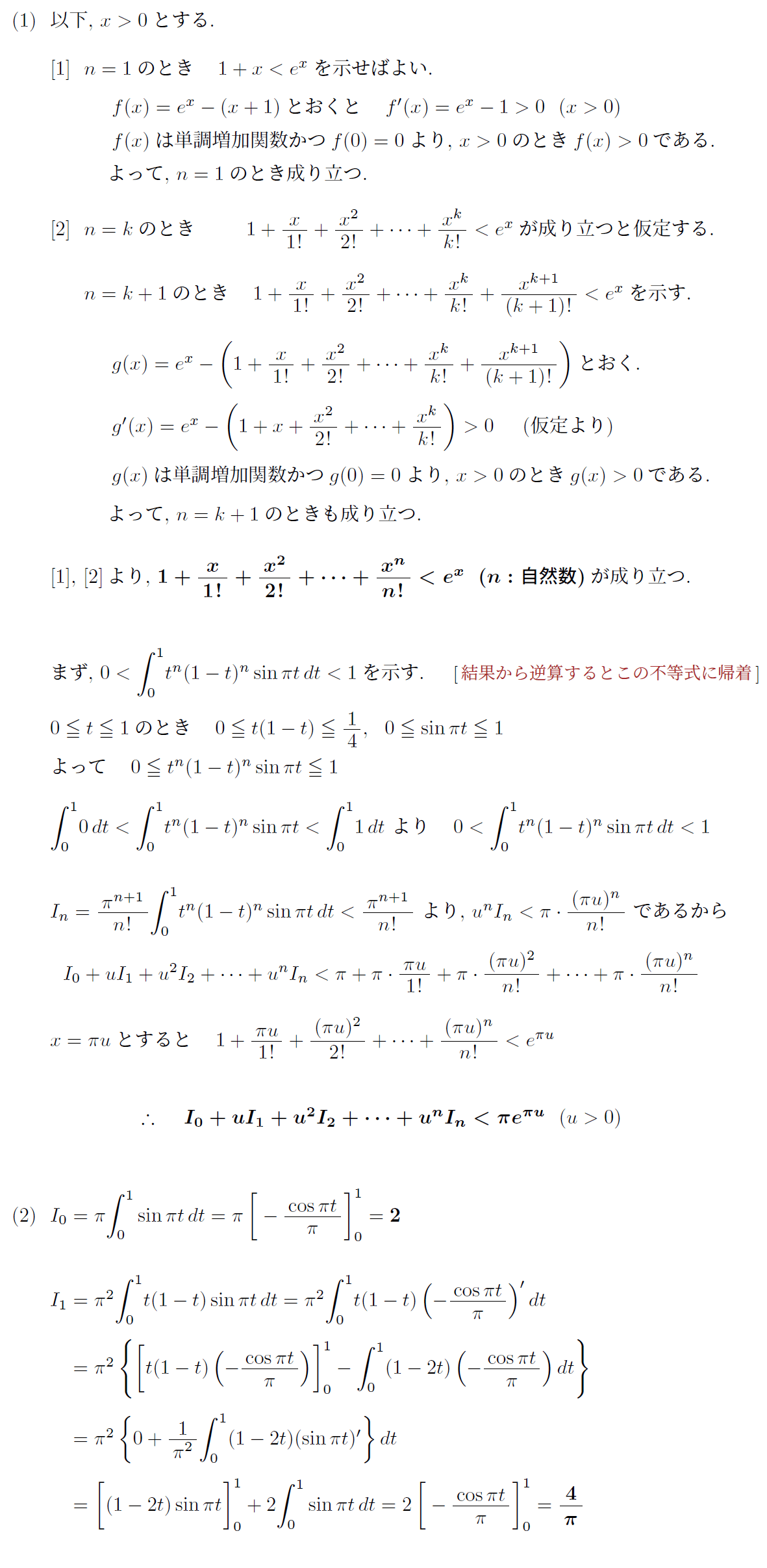
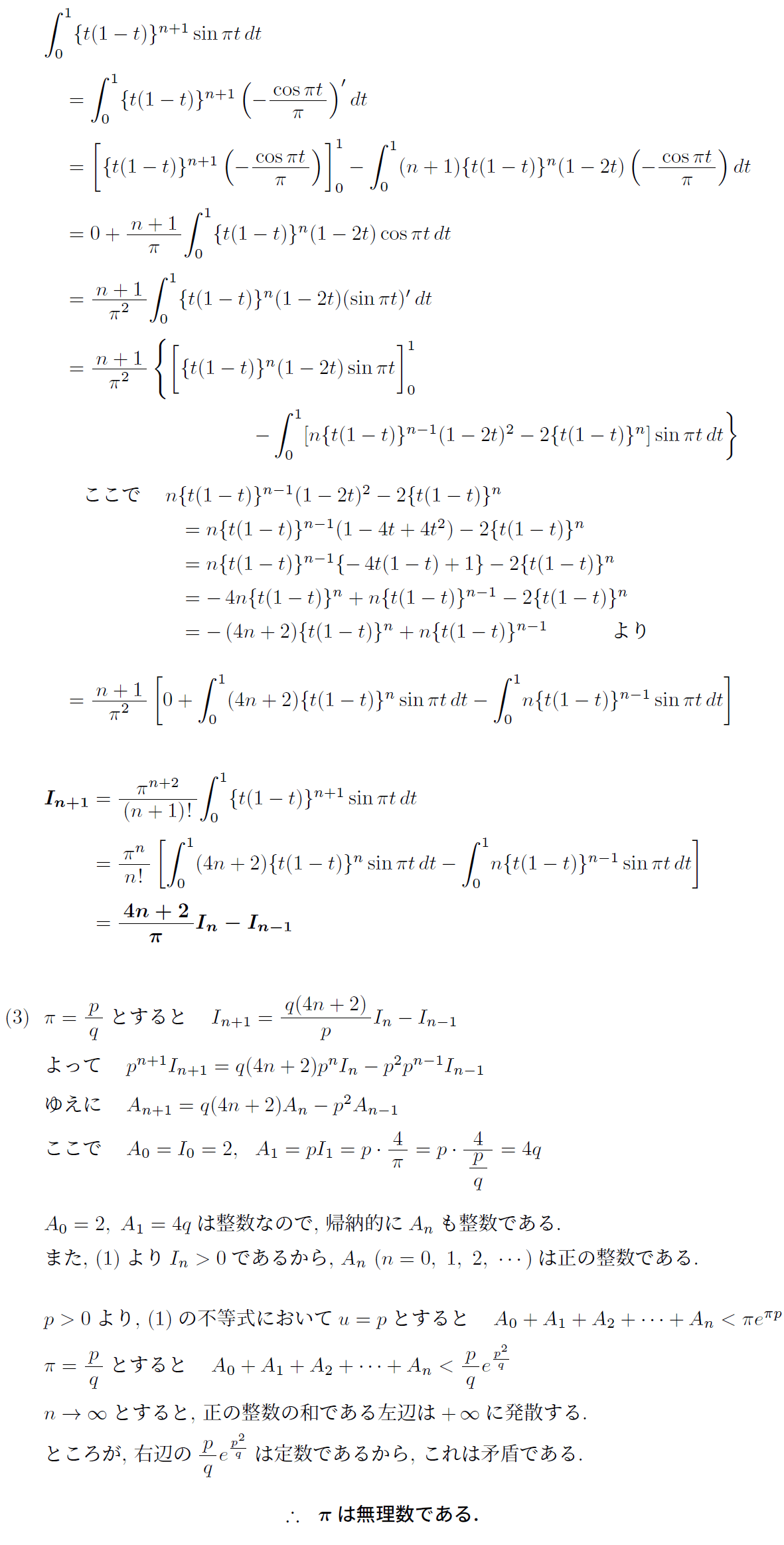
円周率は、1761年、ヨハン・ハインリヒ・ランベルト(ドイツ)によって無理数であることが証明された。

また、1882年、フェルディナント・フォン・リンデマン(ドイツ)によって超越数(有理数係数方程式の解にならない孤高の存在)であることも証明された。

　

大阪大学は、2013年にも円周率に関する問題を出題して伝説を残している。

以下の記事では円周率の近似値の歴史についても触れている。

円周率3の誤解とゆとり教育からの脱却

実は、そもそも超ゆとり教育課程で「円周率を3にする」というのは完全な誤解である。

学習指導要綱には以前から「目的に応じて3を用いて処理できる」という文言があり、概算したいときなどには3として計算するといったことが想定されていた。

しかし、超ゆとり教育課程施行の際に、受験産業が危機感を煽るために「円周率は3.14ではなくおよそ3」と触れ回り、それをメディアが大々的に取り上げたことなどから一般に誤った認識が広まったのである。

賛否あったゆとり教育であったが、国際学力テストでの日本の順位低下などが問題視され、2011年から始まった教育課程では、減り続けてきた授業時間が30年ぶりに増加し、ゆとり教育からの脱却が明確になった。

なお、学力については様々な調査結果があり、ゆとり教育の成果についての確定的な評価は得られていないようである。

円周率の本質

円周率を3とするか3.14とするかは単に計算上の問題であって本質的な問題ではない。

そもそも円周率とは何かを把握するような学習を積み重ねることが何よりも重要である。

実際、次の質問1つでその学生の数学力がある程度推し量れる。

「円周率って何？」

ハイレベルな学生　「（質問の意図を理解して）円の直径と円周長の比です。」

ほとんどの学生　「（自信満々に）3.14！！！」

最後に

世の中には次のようなマニアックな書籍が存在する。

ただただ円周率100万桁を記述しただけの書籍である。乱数表として使ったり、ゾロ目や連番を探して楽しんだりできるとか。ちなみに、100万桁までに3333333や23456789が存在する。

ところどころに小ネタがちりばめられており、なかなか面白い(気付いた？)。