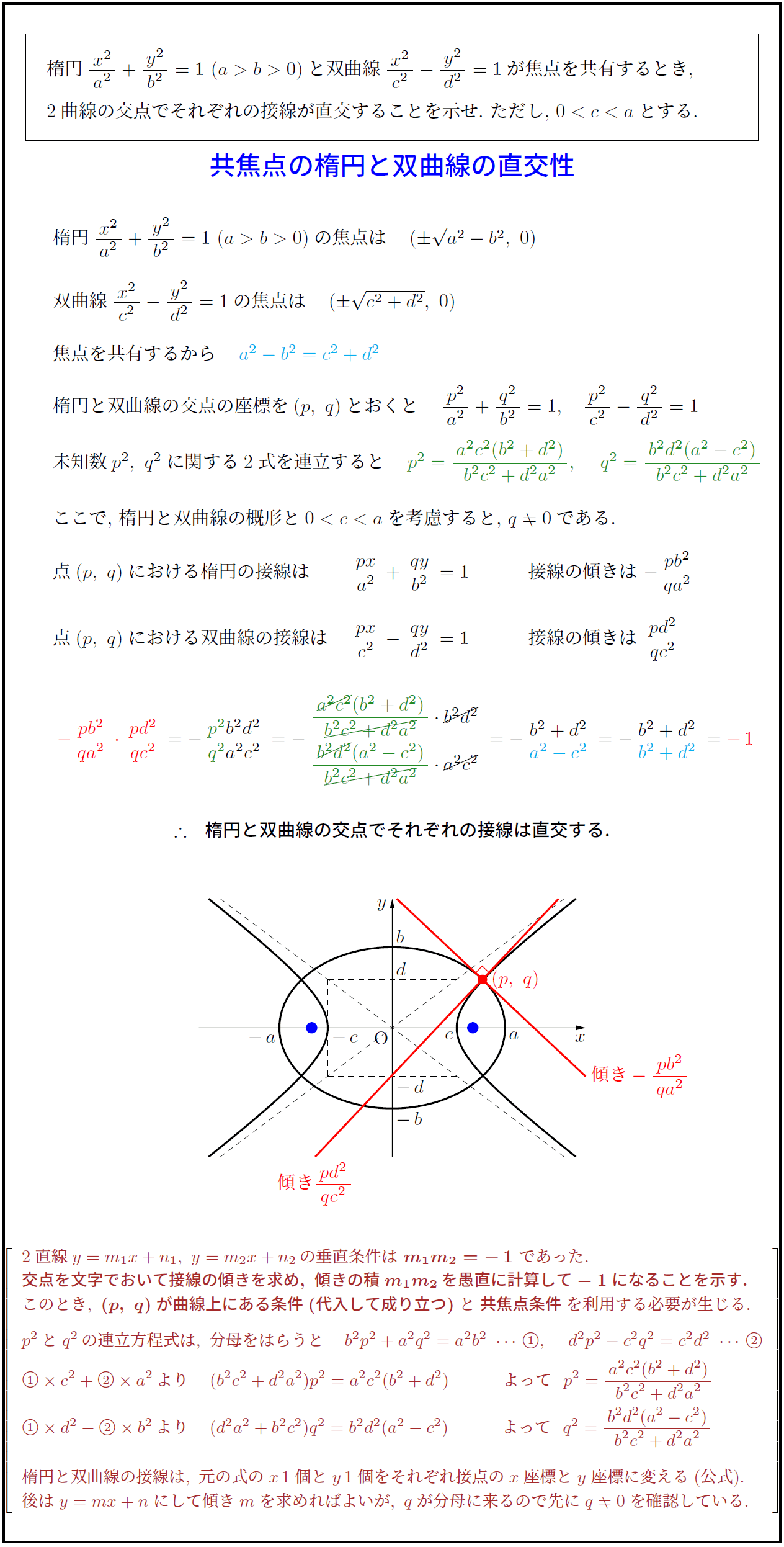
楕円$\bunsuu{x^2}{a^2}+\bunsuu{y^2}{b^2}=1\$と双曲線$\bunsuu{x^2}{c^2}-\bunsuu{y^2}{d^2}=1$が焦点を共有するとき, 2曲線の交点でそれぞれの接線が直交することを示せ.
楕円$\bunsuu{x^2}{a^2}+\bunsuu{y^2}{b^2}=1\ $の焦点は $(\pm\ruizyoukon{a^2-b^2},\ 0)$ \\[1zh]
双曲線$\bunsuu{x^2}{c^2}-\bunsuu{y^2}{d^2}=1$の焦点は $(\pm\ruizyoukon{c^2+d^2},\ 0)$ \\[1zh]
焦点を共有するから a^2-b^2=c^2+d^2
楕円と双曲線の交点の座標を$(p,\ q)$とおくと
未知数$p^2,\ q^2$に関する2式を連立すると
ここで,\ 楕円と双曲線の概形とを考慮すると,\ $q\neqq0$である. \\[1zh]
点$(p,\ q)$における楕円の接線は 接線の傾きは\ $-
点$(p,\ q)$における双曲線の接線は 接線の傾きは\
2直線y=m_1x+n_1,\ y=m_2x+n_2\,の垂直条件は\ \bm{m_1m_2=-\,1}\ であった. \\[.2zh]
\bm{交点を文字でおいて接線の傾きを求め,\ 傾きの積m_1m_2\,を愚直に計算して-1になることを示す.} \\[.2zh]
このとき,\ \bm{(p,\ q)が曲線上にある条件(代入して成り立つ)}と\bm{共焦点条件}を利用する必要が生じる. \\[1zh]
p^2\,とq^2\,の連立方程式は,\ 分母をはらうと
楕円と双曲線の接線は,\ 元の式のx\,1個とy\,1個をそれぞれ接点のx座標とy座標に変える(公式). \\[.2zh]
後はy=mx+nにして傾きmを求めればよいが,\ qが分母に来るので先にq\neqq0を確認している.

