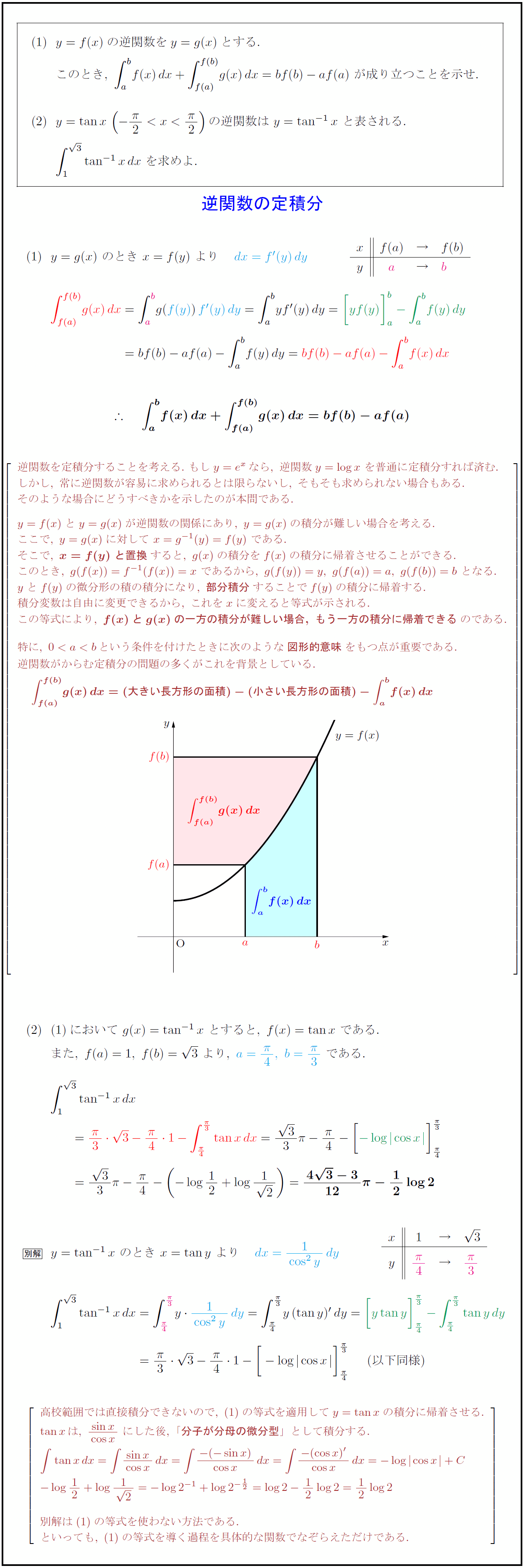
y=f(x)の逆関数をy=g(x)とする.$ $このとき,\ ∫a}{b}f(x)dx+∫f(a)}{f(b)}g(x)dx=bf(b)-af(a)$\ が成り立つことを示せ. $y=tan x(-{π}{2}{π}{2})の逆関数は\ y=tan^{-1}x\ と表される.$ $∫1}{3}tan^{-1}xdx\ を求めよ.$ 逆関数を定積分することを考える.\ もしy=e^xなら,\ 逆関数y=log x\ を普通に定積分すれば済む. しかし,\ 常に逆関数が容易に求められるとは限らないし,\ そもそも求められない場合もある. そのような場合にどうすべきかを示したのが本問である. y=f(x)とy=g(x)が逆関数の関係にあり,\ y=g(x)の積分が難しい場合を考える. ここで,\ y=g(x)に対して\ x=g^{-1}(y)=f(y)\ である. そこで,\ {x=f(y)\ と置換}すると,\ g(x)の積分をf(x)の積分に帰着させることができる. このとき,\ g(f(x))=f^{-1}(f(x))=x\ であるから,\ g(f(y))=y,\ g(f(a))=a,\ g(f(b))=b\ となる. yとf(y)の微分形の積の積分になり,\ {部分積分}することでf(y)の積分に帰着する. 積分変数は自由に変更できるから,\ これをxに変えると等式が示される. この等式により,\ {f(x)とg(x)の一方の積分が難しい場合,\ もう一方の積分に帰着できる}のである. 特に,\ という条件を付けたときに次のような{図形的意味}をもつ点が重要である. 逆関数がからむ定積分の問題の多くがこれを背景としている. $g(x)=tan^{-1}x\ とすると,\ f(x)=tan x\ 高校範囲では直接積分できないので,\ の等式を適用してy=tan xの積分に帰着させる. tan xは,\ {sin x}{cos x}\ にした後,\ 「{分子が分母の微分型}」として積分する. 別解はの等式を使わない方法である. といっても,\ の等式を導く過程を具体的な関数でなぞらえただけである.

