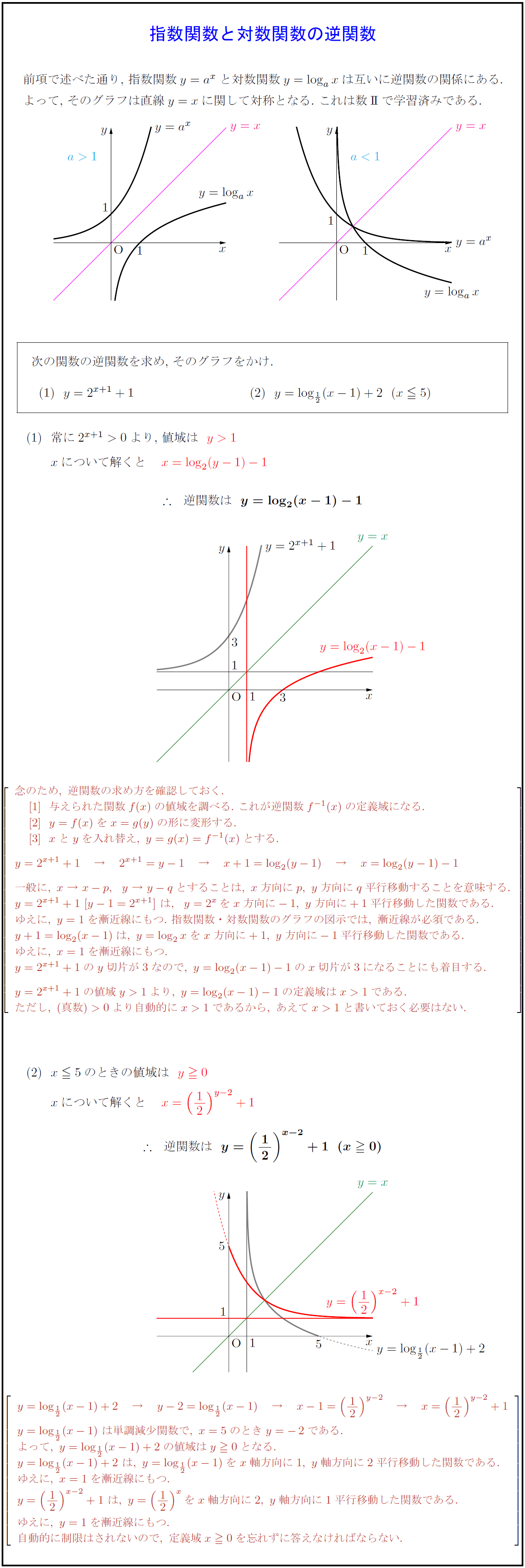
前項で述べた通り,\ 指数関数$y=a^x$と対数関数$y=log_ax$は互いに逆関数の関係にある. よって,\ そのグラフは直線$y=x$に関して対称となる.\ これは数IIで学習済みである. 次の関数の逆関数を求め,\ そのグラフをかけ. \ 逆関数は\ 念のため,\ 逆関数の求め方を確認しておく. 与えられた関数f(x)の値域を調べる.\ これが逆関数f^{-1}(x)の定義域になる. y=f(x)をx=g(y)の形に変形する. [3]xとyを入れ替え,\ y=g(x)=f^{-1}(x)とする. y=2^{x+1}+1 → 2^{x+1}=y-1 → x+1=log₂(y-1) → x=log₂(y-1)-1 一般に,\ x\ →\ x-p,y\ →\ y-qとすることは,\ x方向にp,\ y方向にq平行移動することを意味する. y=2^{x+1}+1\ [y-1=2^{x+1}]\ は,y=2^xをx方向に-1,\ y方向に+1平行移動した関数である. ゆえに,\ y=1を漸近線にもつ.\ 指数関数・対数関数のグラフの図示では,\ 漸近線が必須である. y+1=log₂(x-1)は,\ y=log₂xをx方向に+1,\ y方向に-1平行移動した関数である. ゆえに,\ x=1を漸近線にもつ. y=2^{x+1}+1のy切片が3なので,\ y=log₂(x-1)-1のx切片が3になることにも着目する. y=2^{x+1}+1の値域y>1より,\ y=log₂(x-1)-1の定義域はx>1である. ただし,\ (真数)>0より自動的にx>1であるから,\ あえてx>1と書いておく必要はない. y=log_{1/2}(x-1)\ は単調減少関数で,\ x=5のときy=-2である. よって,\ y=log_{1/2}(x-1)+2の値域はy0となる. y=log_{1/2}(x-1)+2\ は,\ y=log_{1/2}(x-1)をx軸方向に1,\ y軸方向に2平行移動した関数である. ゆえに,\ x=1を漸近線にもつ. y=(12)^{x-2}+1\ は,\ y=(12)^xをx軸方向に2,\ y軸方向に1平行移動した関数である. ゆえに,\ y=1を漸近線にもつ. 自動的に制限はされないので,\ 定義域x0を忘れずに答えなければならない.

