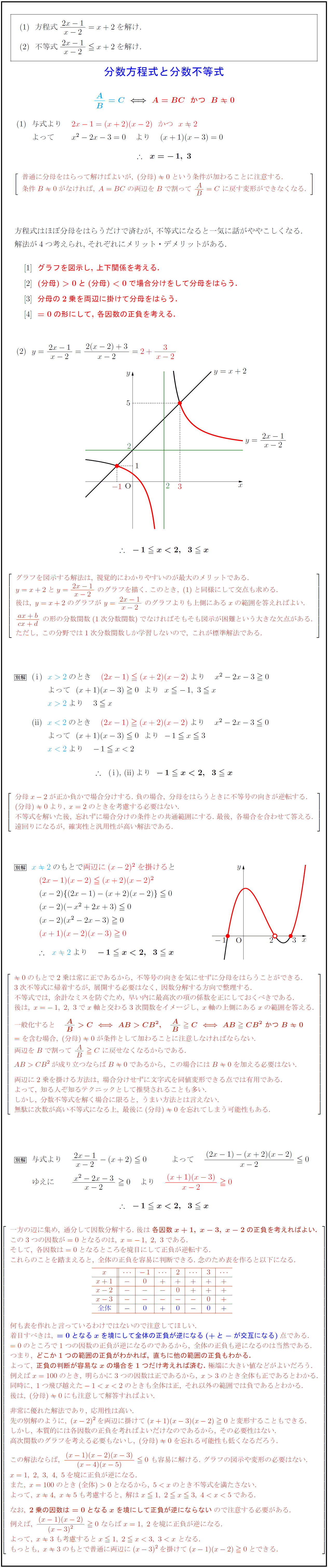
方程式${2x-1}{x-2}=x+2$を解け. 不等式${2x-1}{x-2} x+2$を解け. 分数方程式と分数不等式 普通に分母をはらって解けばよいが,\ (分母)0という条件が加わることに注意する. 条件B0がなければ,\ A=BCの両辺をBで割って\ AB=C\ に戻す変形ができなくなる. 方程式はほぼ分母をはらうだけで済むが,\ 不等式になると一気に話がややこしくなる. 解法が4つ考えられ,\ それぞれにメリット・デメリットがある. グラフを図示し,\ 上下関係を考える. ${(分母)>0}$と${(分母)<0}$で場合分けをして分母をはらう. [3]分母の2乗を両辺に掛けて分母をはらう. [4]${=0}$の形にして,\ 各因数の正負を考える. グラフを図示する解法は,\ 視覚的にわかりやすいのが最大のメリットである. y=x+2とy={2x-1}{x-2}\ のグラフを描く.\ このとき,\ と同様にして交点も求める. 後は,\ y=x+2のグラフが\ y={2x-1}{x-2}\ のグラフよりも上側にあるxの範囲を答えればよい. {ax+b}{cx+d}\ の形の分数関数(1次分数関数)でなければそもそも図示が困難という大きな欠点がある. ただし,\ この分野では1次分数関数しか学習しないので,\ これが標準解法である. }]$ 分母x-2が正か負かで場合分けする.\ 負の場合,\ 分母をはらうときに不等号の向きが逆転する. (分母)0より,\ x=2のときを考慮する必要はない. 不等式を解いた後,\ 忘れずに場合分けの条件との共通範囲にする.\ 最後,\ 各場合を合わせて答える. 遠回りになるが,\ 確実性と汎用性が高い解法である. のもとで両辺に$(x-2)²$を掛ける}と 0のもとで2乗は常に正であるから,\ 不等号の向きを気にせずに分母をはらうことができる. 3次不等式に帰着するが,\ 展開する必要はなく,\ 因数分解する方向で整理する. 不等式では,\ 余計なミスを防ぐため,\ 早い内に最高次の項の係数を正にしておくべきである. 後は,\ x=-1,\ 2,\ 3でx軸と交わる3次関数をイメージし,\ x軸の上側にあるxの範囲を答える. 一般化すると { AB>CAB>CB², AB CAB CB²\ かつ\ B0} =を含む場合,\ (分母)0が条件として加わることに注意しなければならない. 両辺をBで割って\ AB C\ に戻せなくなるからである. AB>CB²が成り立つならばB0であるから,\ この場合にはB0を加える必要はない. 両辺に2乗を掛ける方法は,\ 場合分けせずに文字式を同値変形できる点では有用である. よって,\ 知る人ぞ知るテクニックとして推奨されることも多い. しかし,\ 分数不等式を解く場合に限ると,\ うまい方法とは言えない. 無駄に次数が高い不等式になる上,\ 最後に(分母)0を忘れてしまう可能性もある. 一方の辺に集め,\ 通分して因数分解する.\ 後は{各因数x+1,\ x-3,\ x-2の正負を考えればよい.} この3つの因数が=0となるのは,\ x=-1,\ 2,\ 3である. そして,\ 各因数は=0となるところを境目にして正負が逆転する. これらのことを踏まえると,\ 全体の正負を容易に判断できる.\ 念のため表を作ると以下になる\ 何も表を作れと言っているわけではないので注意してほしい. 着目すべきは,\ {=0となるxを境にして全体の正負が逆になる(+と-が交互になる)点である. =0のところで1つの因数の正負が逆になるのであるから,\ 全体の正負も逆になるのは当然である. つまり,\ {どこか1つの範囲の正負がわかれば,\ 直ちに他の範囲の正負もわかる.} よって,\ {正負の判断が容易なxの場合を1つだけ考えれば済む.}\ 極端に大きい値などがよいだろう. 例えばx=100のとき,\ 明らかに3つの因数は正であるから,\ x>3のとき全体も正であるとわかる. 同時に,\ 1つ飛び越えた-10となるから,\ 5

