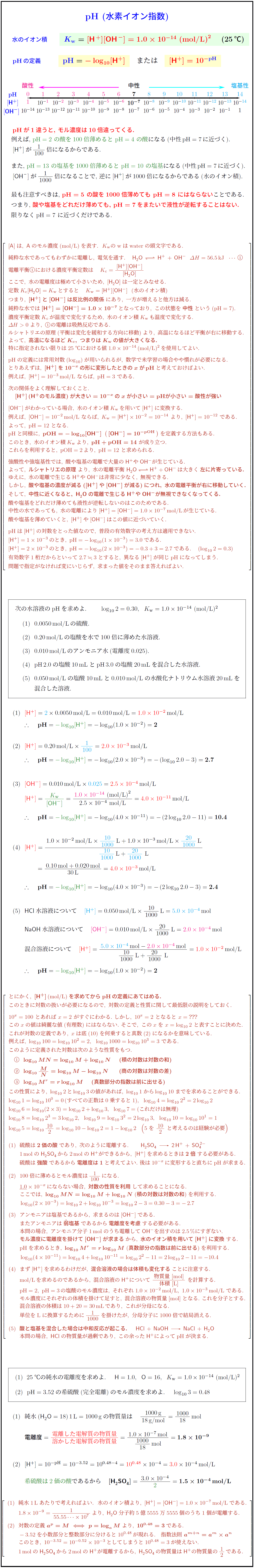
水のイオン積 Kw=[H⁺][OH⁻]=1.0×10⁻¹⁴ (mol/L)² (25℃)
pHの定義 pH=-log₁₀[H⁺] または [H⁺]=10⁻ᵖᴴ
pHが1違うと, モル濃度は10倍違ってくる.
例えば, pH=2の酸を100倍薄めるとpH=4の酸になる(中性pH=7に近づく).
[H⁺]が1/100倍になるからである.
また, pH=13の塩基を1000倍薄めるとpH=10の塩基になる(中性pH=7に近づく).
[OH⁻]が1/1000倍になることで, 逆に[H⁺]が1000倍になるからである(水のイオン積).
最も注意すべきは, pH=5の酸を1000倍薄めてもpH=8にはならないことである.
つまり, 酸や塩基をどれだけ薄めても, pH=7をまたいで液性が逆転することはない.
限りなくpH=7に近づくだけである.
[A]はAのモル濃度(mol/L)を表す. Kwのwはwaterの頭文字である.
純粋な水であってもわずかに電離し, 電気を通す.
H₂O⇄H⁺+OH⁻ ΔH=56.5kJ …①
電離平衡①における濃度平衡定数は
Kc=[H⁺][OH⁻]/[H₂O]
ここで, 水の電離度は極めて小さいため, [H₂O]は一定とみなせる.
定数Kc[H₂O]=Kwとすると
Kw=[H⁺][OH⁻] (水のイオン積)
つまり, [H⁺]と[OH⁻]は反比例の関係にあり, 一方が増えると他方は減る.
純粋な水では[H⁺]=[OH⁻]=1.0×10⁻⁷となっており, この状態を中性という(pH=7).
濃度平衡定数Kcが温度で変化するため, 水のイオン積Kwも温度で変化する.
ΔH>0より, ①の電離は吸熱反応である.
ルシャトリエの原理(平衡は変化を緩和する方向に移動)より, 高温になるほど平衡が右に移動する.
よって, 高温になるほどKc, つまりKwの値が大きくなる.
特に指定されない限りは25℃における値1.0×10⁻¹⁴(mol/L)²を使用してよい.
pHの定義には常用対数(log₁₀)が用いられるが, 数学で未学習の場合やや慣れが必要になる.
とりあえずは, [H⁺]を10⁻ˣの形に変形したときのxがpHと考えておけばよい.
例えば, [H⁺]=10⁻³ mol/LならばpH=3である.
次の関係をよく理解しておくこと.
H⁺
が大きい=10⁻ˣのxが小さい=pHが小さい=酸性が強い
[OH⁻]がわかっている場合, 水のイオン積Kwを用いて[H⁺]に変換する.
例えば, [OH⁻]=10⁻² mol/Lならば, Kw=[H⁺]×10⁻²=10⁻¹⁴より, [H⁺]=10⁻¹²である.
よってpH=12となる.
pHと同様に, pOH=-log₁₀[OH⁻] ([OH⁻]=10⁻ᵖᴼᴴ)を定義する方法もある.
このとき, 水のイオン積Kwより, pH+pOH=14が成り立つ.
これらを利用すると, pOH=2よりpH=12と求められる.
強酸性や強塩基性では, 酸や塩基の電離で大量のH⁺やOH⁻が生じている.
よって, ルシャトリエの原理より, 水の電離平衡 H₂O⇄H⁺+OH⁻ は大きく左に片寄っている.
ゆえに, 水の電離で生じるH⁺やOH⁻は非常に少なく, 無視できる.
しかし, 酸や塩基の濃度が減る([H⁺]や[OH⁻]が減る)につれ, 水の電離平衡が右に移動していく.
そして, 中性に近くなると, H₂Oの電離で生じるH⁺やOH⁻が無視できなくなってくる.
酸や塩基をどれだけ薄めても液性が逆転しないのはこのためである.
中性の水であっても, 水の電離により[H⁺]=[OH⁻]=1.0×10⁻⁷ mol/Lが生じている.
酸や塩基を薄めていくと, [H⁺]や[OH⁻]はこの値に近づいていく.
pHは[H⁺]の対数をとった値なので, 普段の有効数字の考え方は適用できない.
[H⁺]=1×10⁻³のとき, pH=-log₁₀(1×10⁻³)=3.0である.
[H⁺]=2×10⁻³のとき, pH=-log₁₀(2×10⁻³)=-(0.3-3)=2.7である (log₁₀2=0.3).
有効数字1桁だからといって2.7≈3とすると, 異なる[H⁺]が同じpHになってしまう.
問題で指定がなければ変にいじらず, 求まった値をそのまま答えればよい.
次の水溶液のpHを求めよ.
log₁₀2=0.30, Kw=1.0×10⁻¹⁴ (mol/L)²
(1) 0.0050 mol/Lの硫酸
(2) 0.20 mol/Lの塩酸を水で100倍に薄めた水溶液
(3) 0.010 mol/Lのアンモニア水(電離度0.025)
(4) pH2.0の塩酸10mLとpH3.0の塩酸20mLを混合した水溶液
(5) 0.050 mol/Lの塩酸10mLと0.010 mol/Lの水酸化ナトリウム水溶液20mLを混合した溶液
(1) [H⁺]=2×0.0050=0.010=1.0×10⁻² mol/L
∴ pH=-log₁₀[H⁺]=-log₁₀(1.0×10⁻²)=2
(2) [H⁺]=0.20×(1/100)=2.0×10⁻³ mol/L
∴ pH=-log₁₀[H⁺]=-log₁₀(2.0×10⁻³)=-(log₁₀2.0-3)=2.7
(3) [OH⁻]=0.010×0.025=2.5×10⁻⁴ mol/L
[H⁺]=Kw/[OH⁻]=1.0×10⁻¹⁴/2.5×10⁻⁴=4.0×10⁻¹¹ mol/L
∴ pH=-log₁₀[H⁺]=-log₁₀(4.0×10⁻¹¹)=-(2log₁₀2.0-11)=10.4
(4) [H⁺]=(1.0×10⁻²×10/1000+1.0×10⁻³×20/1000)/(10/1000+20/1000)=4.0×10⁻³ mol/L
∴ pH=-log₁₀[H⁺]=-log₁₀(4.0×10⁻³)=-(2log₁₀2.0-3)=2.4
(5) HCl: [H⁺]=0.050×10/1000=5.0×10⁻⁴ mol
NaOH: [OH⁻]=0.010×20/1000=2.0×10⁻⁴ mol
混合溶液: [H⁺]=(5.0×10⁻⁴-2.0×10⁻⁴)/(10/1000+20/1000)=1.0×10⁻² mol/L
∴ pH=-log₁₀[H⁺]=-log₁₀(1.0×10⁻²)=2
とにかく, H⁺
を求めてからpHの定義にあてはめる.
このときに対数の扱いが必要になるので, 対数の定義と性質に関して最低限の説明をしておく.
10ˣ=100 とあれば x=2 がすぐにわかる.
しかし, 10ˣ=2 となると x=?
このxの値は有理数にならない.
そこで, このxを x=log₁₀2 と表すことに決めた.
これが対数の定義であり, xは底(10)を何乗すると真数(2)になるかを意味している.
例:log₁₀100=log₁₀10²=2, log₁₀1000=3
対数の性質:
① log₁₀(MN)=log₁₀M+log₁₀N(積の対数は対数の和)
② log₁₀(M/N)=log₁₀M−log₁₀N(商の対数は対数の差)
③ log₁₀(Mʳ)=rlog₁₀M(指数は前に出せる)
これにより, log₁₀2, log₁₀3があればlog₁₀1〜log₁₀10まで求められる.
log₁₀1=0, log₁₀4=2log₁₀2, log₁₀6=log₁₀2+log₁₀3,
log₁₀8=3log₁₀2, log₁₀9=2log₁₀3, log₁₀10=1,
log₁₀5=1−log₁₀2 (5を10/2と考えるのは経験が必要).
(1) 硫酸は2価の酸であり, H₂SO₄→2H⁺+SO₄²⁻
1molのH₂SO₄から2molのH⁺ができるから, [H⁺]は2倍する.
硫酸は強酸なので電離度は1と考えてよい.
(2) 100倍に薄めるとモル濃度は1/100になる.
1.0×10⁻ˣにならない場合, 対数の性質を利用する.
log₁₀(2×10⁻³)=log₁₀2+log₁₀10⁻³=0.30−3=−2.7
(3) アンモニアは塩基であり, 求まるのは[OH⁻]である.
また弱塩基なので電離度を考慮する.
モル濃度に電離度を掛けて[OH⁻]を求め, 水のイオン積で[H⁺]へ変換する.
log₁₀(4×10⁻¹¹)=log₁₀4+log₁₀10⁻¹¹=2log₁₀2−11=−10.4
(4) 混合溶液では体積変化に注意する.
モル濃度×体積で物質量を出し, 合計を全体の体積で割る.
(5) 酸と塩基を混合した場合は中和反応が起こる.
HCl+NaOH→NaCl+H₂O
この場合HClの物質量が過剰であり, 余ったH⁺がpHを決める.
(1) 25℃の純水の電離度を求めよ.
H=1.0, O=16, Kw=1.0×10⁻¹⁴ (mol/L)²
(2) pH=3.52の希硫酸(完全電離)のモル濃度を求めよ.
log₁₀3=0.48
(1) 純水(H₂O=18) 1L=1000g
物質量=1000/18 mol
電離度=電離した電解質の物質量/溶かした電解質の物質量=1.0×10⁻⁷/(1000/18)=1.8×10⁻⁹
(2) [H⁺]=10⁻ᵖᴴ=10⁻³⋅⁵²=10^(0.48−4)=3.0×10⁻⁴ mol/L
希硫酸は2価の酸だから [H₂SO₄]=3.0×10⁻⁴/2=1.5×10⁻⁴ mol/L
(1) 水のイオン積より, [H⁺]=[OH⁻]=1.0×10⁻⁷ mol/L
1.8×10⁻⁹=1/(55.55…×10⁷)より, 水分子約5億5千万個に1個が電離する.
(2) 対数の定義 aᵖ=M ⇔ p=logₐM より 10^0.48=3 である.
-3.52を小数と整数に分けると10^0.48が現れる(指数法則 a^(m+n)=a^m×a^n).
H₂SO₄1mol→2molH⁺なので, H₂SO₄の物質量はH⁺の1/2である.

