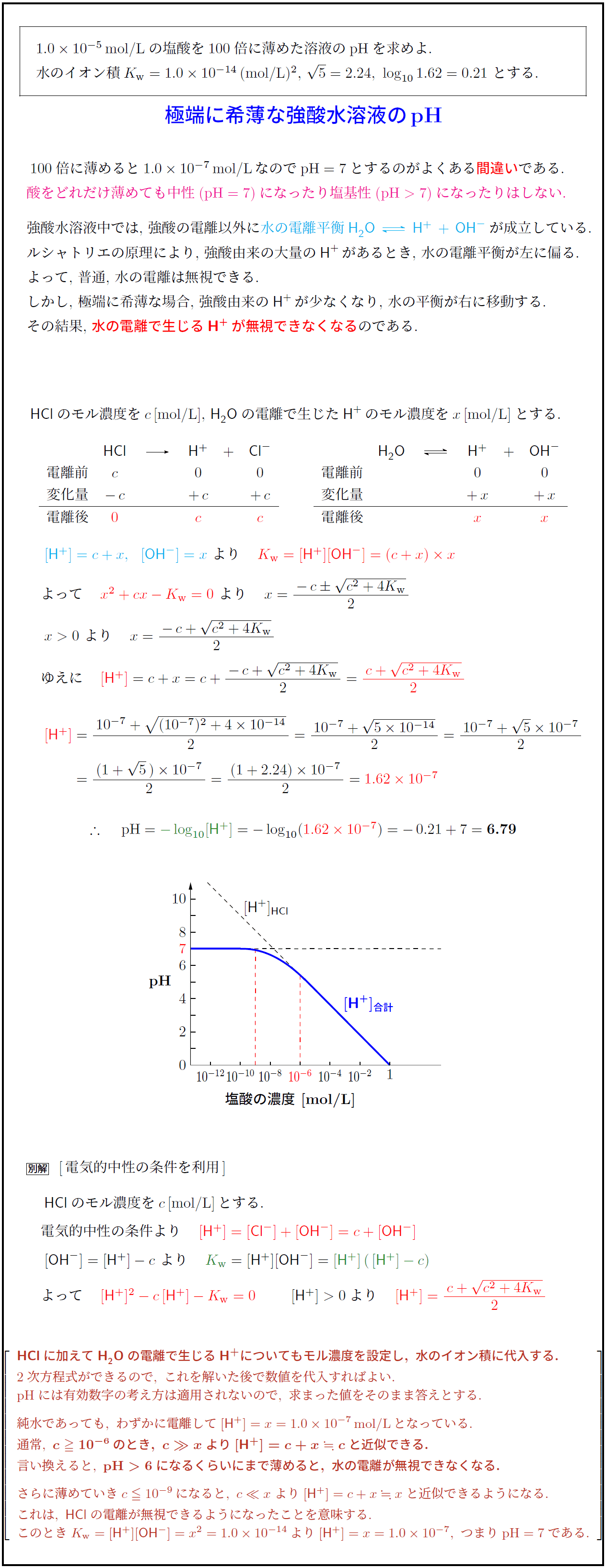
1.0\times10^{-5}$\,mol/Lの塩酸を100倍に薄めた溶液のpHを求めよ. \\[.2zh]
\hspace{.5zw}水のイオン積$K_{\text{w}}=1.0\times10^{-14}$\,(mol/L)$^2$,\ $\ruizyoukon5=2.24,\ \log_{10}1.62=0.21$\ とする. 極端に希薄な強酸水溶液のpH}}}} \\\\[.5zh]
100倍に薄めると$1.0\times10^{-7}$\,mol/L\,なので$\text{pH}=7$とするのがよくある\textbf{\textcolor{red}{間違い}}である. \\[.2zh]
\textcolor{magenta}{酸をどれだけ薄めても中性($\text{pH}=7$)になったり塩基性($\text{pH}>7$)になったりはしない.} \\[1zh]
強酸水溶液中では,\ 強酸の電離以外に\textcolor{cyan}{水の電離平衡$\ce{H2O}\,\ce{<=>}\,\ce{H+}\,+\,\ce{OH-}$}が成立している. \\[.2zh]
ルシャトリエの原理により,\ 強酸由来の大量の\ce{H+}\,があるとき,\ 水の電離平衡が左に偏る. \\[.2zh]
よって,\ 普通,\ 水の電離は無視できる. \\[.2zh]
しかし,\ 極端に希薄な場合,\ 強酸由来の\ce{H+}\,が少なくなり,\ 水の平衡が右に移動する. \\[.2zh]
その結果,\ \textbf{\textcolor{red}{水の電離で生じる\ce{H+}\,が無視できなくなる}}のである. \\\\\\\\
\ce{HCl}のモル濃度を$c$\,[mol/L],\ \ce{H2O}の電離で生じた\ce{H+}\,のモル濃度を$x$\,[mol/L]とする. \\
[\,電気的中性の条件を利用\,] \\[1zh]
\ce{HCl}のモル濃度を$c$\,[mol/L]\,とする. \\[.5zh]
電気的中性の条件より $\textcolor{red}{[\ce{H+}]=[\ce{Cl-}]+[\ce{OH-}]=c+[\ce{OH-}]}$ \\[.5zh]
\bm{\ce{HCl}に加えて\ce{H2O}の電離で生じる\ce{H+}についてもモル濃度を設定し,\ 水のイオン積に代入する.} \\[.4zh]
2次方程式ができるので,\ これを解いた後で数値を代入すればよい. \\[.2zh]
\text{pH}には有効数字の考え方は適用されないので,\ 求まった値をそのまま答えとする. \\[1zh]
純水であっても,\ わずかに電離して[\ce{H+}]=x=1.0\times10^{-7}\,\text{mol/L}\,となっている. \\[.4zh]
通常,\ \bm{c\geqq10^{-6}\,のとき,\ c\gg xより[\ce{H+}]=c+x\kinzi cと近似できる.} \\[.4zh]
言い換えると,\ \bm{\textbf{pH}>6になるくらいにまで薄めると,\ 水の電離が無視できなくなる.} \\[1zh]
さらに薄めていきc\leqq10^{-9}\,になると,\ c\ll xより[\ce{H+}]=c+x\kinzi xと近似できるようになる. \\[.4zh]
これは,\ \ce{HCl}の電離が無視できるようになったことを意味する. \\[.2zh]
このときK_{\text w}=[\ce{H+}][\ce{OH-}]=x^2=1.0\times10^{-14}\,より[\ce{H+}]=x=1.0\times10^{-7},\ つまり\text{pH}=7である.

