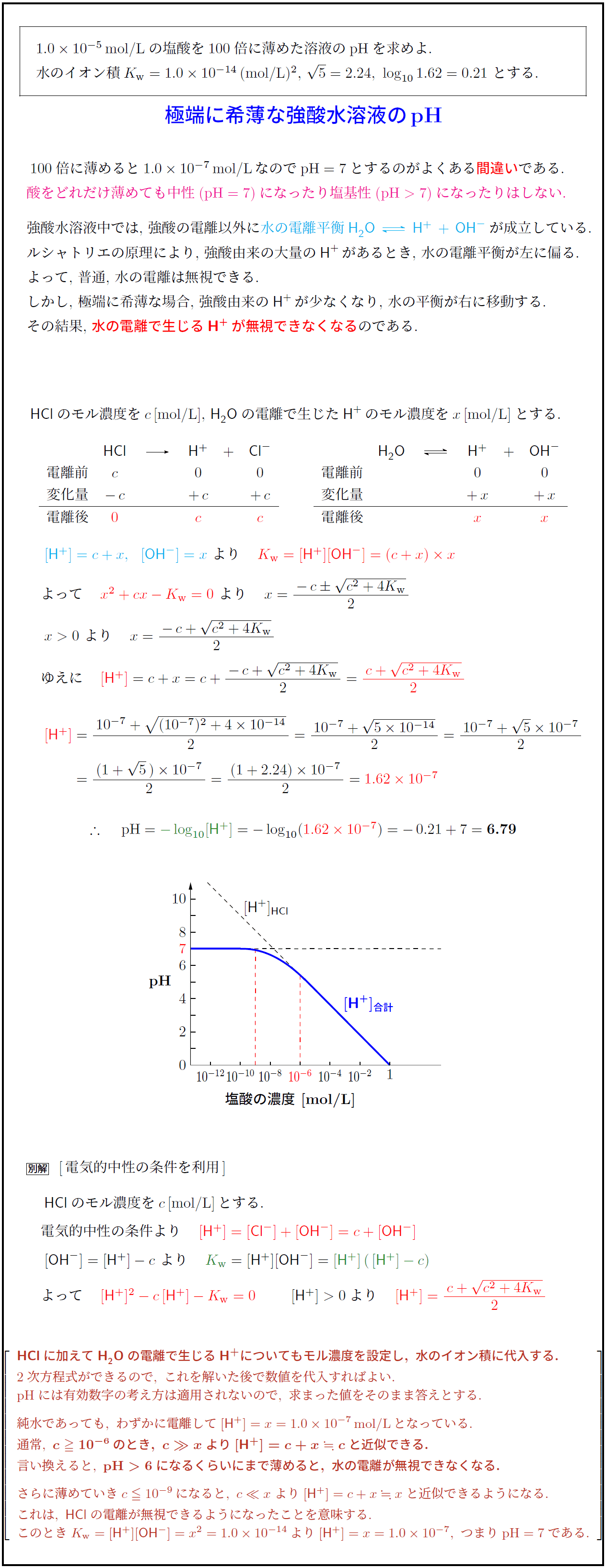
1.0×10⁻⁵ mol/Lの塩酸を100倍に薄めた溶液のpHを求めよ.
水のイオン積 Kw = 1.0×10⁻¹⁴ (mol/L)², √5 = 2.24, log₁₀1.62 = 0.21 とする.
100倍に薄めると1.0×10⁻⁷ mol/LなのでpH=7とするのがよくある間違いである.
酸をどれだけ薄めても中性(pH=7)になったり塩基性(pH>7)になったりはしない.
強酸水溶液中では, 強酸の電離以外に水の電離平衡 H₂O ⇄ H⁺ + OH⁻ が成立している.
ルシャトリエの原理により, 強酸由来の大量のH⁺があるとき, 水の電離平衡が左に偏る.
よって, 普通, 水の電離は無視できる.
しかし, 極端に希薄な場合, 強酸由来のH⁺が少なくなり, 水の電離平衡が右に移動する.
その結果, 水の電離で生じるH⁺が無視できなくなるのである.
HClのモル濃度をc [mol/L], H₂Oの電離で生じたH⁺のモル濃度をx [mol/L]とする.
HCl → 100%電離
電離前 c 変化量 −c 電離後 0
H⁺ 電離前 0 → 変化量 +c → 電離後 c
Cl⁻ 電離前 0 → 変化量 +c → 電離後 c
H₂O ⇄ H⁺ + OH⁻
電離前 多量
H⁺ 電離前 c → 変化量 +x → 電離後 c+x
OH⁻ 電離前 0 → 変化量 +x → 電離後 x
[H⁺] = c + x , [OH⁻] = x より
Kw = [H⁺][OH⁻] = (c + x) × x
したがって
x² + c x − Kw = 0 より
x = (−c ± √(c² + 4Kw)) / 2
x > 0 より
x = (−c + √(c² + 4Kw)) / 2
したがって
[H⁺] = c + x = c + (−c + √(c² + 4Kw)) / 2 = (c + √(c² + 4Kw)) / 2
[H⁺] = (10⁻⁷ + √((10⁻⁷)² + 4×10⁻¹⁴)) / 2
= (10⁻⁷ + √(5×10⁻¹⁴)) / 2
= (10⁻⁷ + √5 × 10⁻⁷) / 2
= ((1 + √5) × 10⁻⁷) / 2
= ((1 + 2.24) × 10⁻⁷) / 2
= 1.62×10⁻⁷
∴ pH = −log₁₀[H⁺] = −log₁₀(1.62×10⁻⁷) = −0.21 + 7 = 6.79
別解(電気的中性の条件を利用)
HClは100%電離するから, モル濃度をc [mol/L]とすると [Cl⁻] = c
電気的中性の条件より [H⁺] = [Cl⁻] + [OH⁻] = c + [OH⁻]
[OH⁻] = [H⁺] − c より
Kw = [H⁺][OH⁻] = [H⁺]([H⁺] − c)
したがって
[H⁺]² − c[H⁺] − Kw = 0
[H⁺] > 0 より
[H⁺] = (c + √(c² + 4Kw)) / 2
【補足】
HClに加えてH₂Oの電離で生じるH⁺についてもモル濃度を設定し, 水のイオン積に代入する.
2次方程式ができるので, これを解いた後で数値を代入すればよい.
pHには有効数字の考え方は適用されないので, 求まった値をそのまま答えとする.
純水であっても, わずかに電離して [H⁺] = [OH⁻] = x = 10⁻⁷ mol/L (pH=7) となっている.
通常, c ≥ 10⁻⁶ のとき, c ≫ x より [H⁺] = c + x ≒ c と近似できる.
言い換えると, pH > 6 になるくらいにまで薄めると, 水の電離が無視できなくなる.
さらに薄めていき c ≤ 10⁻⁹ になると, c ≪ x より [H⁺] = c + x ≒ x と近似できるようになる.
これは, 逆にHClの電離が無視できるようになったことを意味する.
このとき Kw = [H⁺][OH⁻] ≒ x² = 1.0×10⁻¹⁴ より [H⁺] ≒ x = 1.0×10⁻⁷, つまり pH ≒ 7 である.

