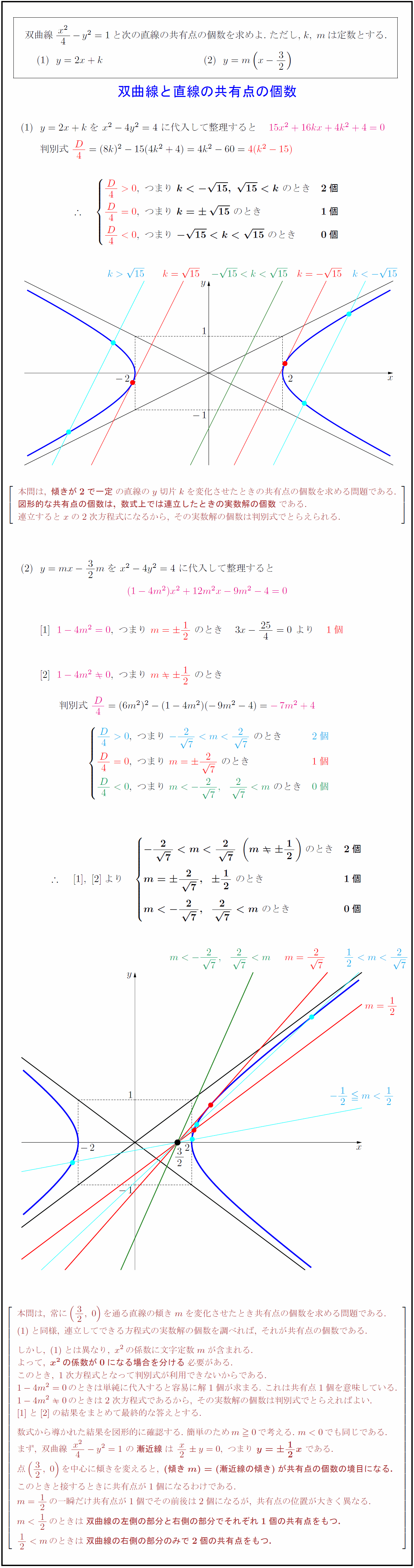
双曲線${x²}{4}-y²=1$と次の直線の共有点の個数を求めよ.\ ただし,\ $k,\ m$は定数とする. $y=2x+k$ $y=m(x-32)$ $y=2x+kを\ x²-4y²=4\ に代入して整理すると 15x²+16kx+4k²+4=0}$ $判別式\ D4}=(8k)²-15(4k²+4)=4k²-60=4(k²-15)}$ 本問は,\ {傾きが2で一定}の直線のy切片kを変化させたときの共有点の個数を求める問題である. {図形的な共有点の個数は,\ 数式上では連立したときの実数解の個数}である. 連立するとxの2次方程式になるから,\ その実数解の個数は判別式でとらえられる. }]$ $y=mx-32mを\ x²-4y²=4\ に代入して整理すると$ $(1-4m²)x²+12m²x-9m²-4=0}$} $1-4m²=0},\ つまり\ m=12}\ のとき 3x-{25}{4}=0\ より 1個}$ $1-4m²0},\ つまり\ m12}\ のとき$ $判別式\ D4}=(6m²)²-(1-4m²)(-9m²-4)=-7m²+4}$ 本問は,\ 常に(32,\ 0)を通る直線の傾きmを変化させたとき共有点の個数を求める問題である. と同様,\ 連立してできる方程式の実数解の個数を調べれば,\ それが共有点の個数である. しかし,\ とは異なり,\ x²の係数に文字定数mが含まれる. よって,\ {x²の係数が0になる場合を分ける}必要がある. このとき,\ 1次方程式となって判別式が利用できないからである. 1-4m²=0のときは単純に代入すると容易に解1個が求まる.\ これは共有点1個を意味している. 1-4m²0のときは2次方程式であるから,\ その実数解の個数は判別式でとらえればよい. との結果をまとめて最終的な答えとする. 数式から導かれた結果を図形的に確認する.\ 簡単のためm0で考える.\ m0でも同じである. まず,\ 双曲線\ {x²}{4}-y²=1\ の{漸近線}は\ x2 y=0,\ つまり\ {y=12x}\ である. 点(32,\ 0)を中心に傾きを変えると,\ {(傾きm)=(漸近線の傾き)が共有点の個数の境目になる.} このときと接するときに共有点が1個になるわけである. m=12の一瞬だけ共有点が1個でその前後は2個になるが,\ 共有点の位置が大きく異なる. m12のときは{双曲線の左側の部分と右側の部分でそれぞれ1個の共有点をもつ.} 12mのときは{双曲線の右側の部分のみで2個の共有点をもつ.}

