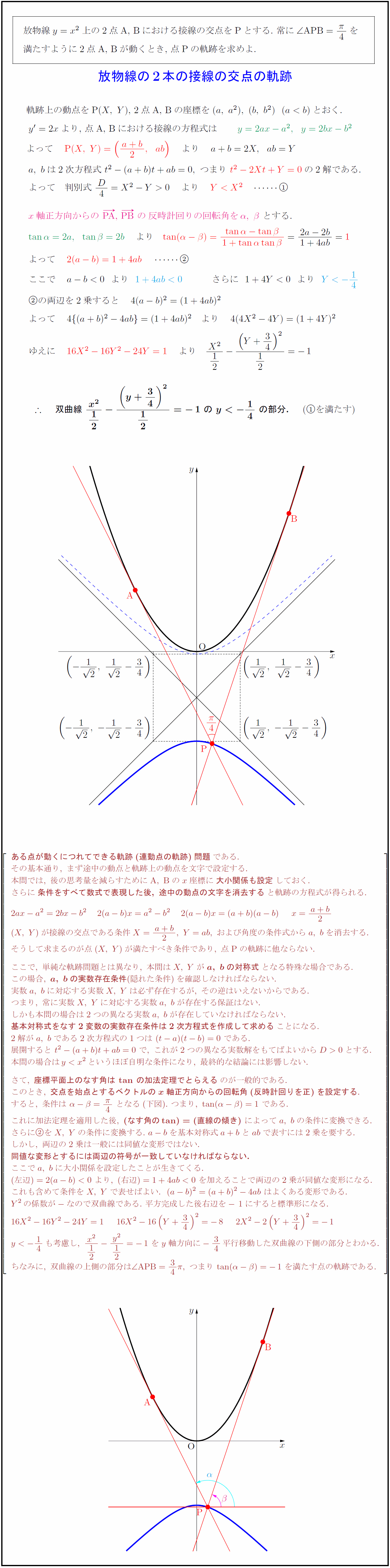
放物線$y=x²$上の2点A,\ Bにおける接線の交点をPとする.\ 常に$∠{APB}={π}{4}$を 満たすように2点A,\ Bが動くとき,\ 点Pの軌跡を求めよ. 軌跡上の動点をP$(X,\ Y)$,\ 2点A,\ Bの座標を$(a,\ a²),\ (b,\ b²)(ab)$とおく. $y’=2x$より,\ 点A,\ Bにおける接線の方程式は $y=2ax-a²,y=2bx-b²}$ よって P$(X,\ Y)=({a+b}{2},ab)$} より $a+b=2X,ab=Y$ $a,\ bは2次方程式\ t²-(a+b)t+ab=0,\ つまり\ t²-2Xt+Y=0}$の2解である. $よって 判別式\ D4=X²-Y0 より YX²} $ $x軸正方向からの$\ PA},\ PB\ の$反時計回りの回転角をα,\ β$}\ とする. $tanα=2a,tanβ=2b} より tan(α-β)={tanα-tanβ}{1+tanαtanβ={2a-2b}{1+4ab}=1}$ $よって 2(a-b)=1+4ab} $ $の両辺を2乗すると 4(a-b)²=(1+4ab)²$ $よって 4{(a+b)²-4ab}=(1+4ab)² より 4(4X²-4Y)=(1+4Y)²$ $ゆえに 16X²-16Y²-24Y=1} より {X²}{12}-{(Y+34)²}{12}=-1$ $ {双曲線\ {x²}{12}-{(y+34)²}{12}=-1\ の\ y-14\ の部分.} (を満たす)$} {ある点が動くにつれてできる軌跡(連動点の軌跡)問題}である. その基本通り,\ まず途中の動点と軌跡上の動点を文字で設定する. 本問では,\ 後の思考量を減らすために{A,\ B}のx座標に{大小関係も設定}しておく. さらに{条件をすべて数式で表現した後,\ 途中の動点の文字を消去する}と軌跡の方程式が得られる. 2ax-a²=2bx-b² 2(a-b)x=a²-b² 2(a-b)x=(a+b)(a-b) x={a+b}{2} (X,\ Y)が接線の交点である条件X={a+b}{2},\ Y=ab,\ および角度の条件式からa,\ bを消去する. そうして求まるのが点(X,\ Y)が満たすべき条件であり,\ 点{P}の軌跡に他ならない. ここで,\ 単純な軌跡問題とは異なり,\ 本問はX,\ Yが{a,\ bの対称式}となる特殊な場合である. この場合,\ {a,\ bの実数存在条件}(隠れた条件)を確認しなければならない. 実数a,\ bに対応する実数X,\ Yは必ず存在するが,\ その逆はいえないからである. つまり,\ 常に実数X,\ Yに対応する実数a,\ bが存在する保証はない. しかも本問の場合は2つの異なる実数a,\ bが存在していなければならない. {基本対称式をなす2変数の実数存在条件は2次方程式を作成して求める}ことになる. 2解がa,\ bである2次方程式の1つは\ (t-a)(t-b)=0\ である. 展開すると\ t²-(a+b)t+ab=0\ で,\ これが2つの異なる実数解をもてばよいからD0とする. 本問の場合はyx²というほぼ自明な条件になり,\ 最終的な結論には影響しない. さて,\ {座標平面上のなす角はtanの加法定理でとらえる}のが一般的である. このとき,\ {交点を始点とするベクトルのx軸正方向からの回転角(反時計回りを正)を設定する}. すると,\ 条件は\ α-β={π}{4}\ となる(下図).\ つまり,\ tan(α-β)=1\ である. これに加法定理を適用した後,\ {(なす角のtan)=(直線の傾き)}\ によってa,\ bの条件に変換できる. さらにをX,\ Yの条件に変換する.\ a-bを基本対称式a+bとabで表すには2乗を要する. しかし,\ 両辺の2乗は一般には同値な変形ではない. {同値な変形とするには両辺の符号が一致していなければならない.} ここでa,\ bに大小関係を設定したことが生きてくる. (左辺)=2(a-b)0\ より,\ (右辺)=1+4ab0\ を加えることで両辺の2乗が同値な変形になる. これも含めて条件をX,\ Yで表せばよい.(a-b)²=(a+b)²-4ab\ はよくある変形である. Y²の係数が-なので双曲線である.\ 平方完成した後右辺を-1にすると標準形になる. 16X²-16Y²-24Y=1 16X²-16(Y+34)²=-8 2X²-2(Y+34)²=-1 y-14も考慮し,\ {x²}{12}-{y²}{12}=-1\ をy軸方向に-34平行移動した双曲線の下側の部分とわかる. ちなみに,\ 双曲線の上側の部分は∠{APB}=34π,\ つまりtan(α-β)=-1\ を満たす点の軌跡である.

