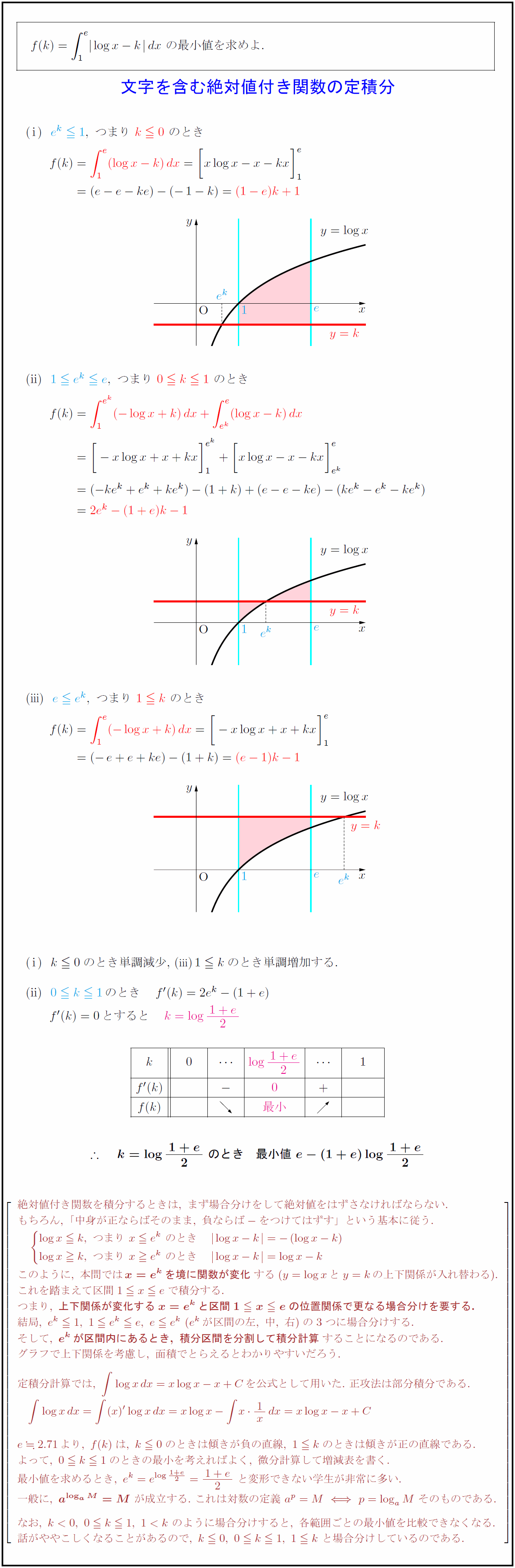
f(k)=∫1}{e}log x-k}dx\ の最小値を求めよ.$ 絶対値付き関数を積分するときは,\ まず場合分けをして絶対値をはずさなければならない. もちろん,\ 「中身が正ならばそのまま,\ 負ならば-をつけてはずす」という基本に従う. このように,\ 本問では{x=e^kを境に関数が変化}する(y=log xとy=kの上下関係が入れ替わる). これを踏まえて区間1 x eで積分する. つまり,\ {上下関係が変化するx=e^kと区間1 x eの位置関係で更なる場合分けを要する.} 結局,\ e^k1,\ 1 e^k e,\ e e^k\ (e^kが区間の左,\ 中,\ 右)の3つに場合分けする. そして,\ {e^kが区間内にあるとき,\ 積分区間を分割して積分計算}することになるのである. グラフで上下関係を考慮し,\ 面積でとらえるとわかりやすいだろう. 定積分計算では,\ ∫log xdx=xlog x-x+Cを公式として用いた.\ 正攻法は部分積分である. ∫log xdx=∫(x)’log xdx=xlog x-∫x1xdx=xlog x-x+C e2.71より,\ f(k)は,\ k0のときは傾きが負の直線,\ 1 kのときは傾きが正の直線である. よって,\ 0 k1のときの最小を考えればよく,\ 微分計算して増減表を書く. 最小値を求めるとき,\ e^k=e^{log1+e}{2={1+e}{2}\ と変形できない学生が非常に多い. 一般に,\ {a^{log _aM}=M}\ が成立する.\ これは対数の定義\ a^p=Mp=log_a M\ そのものである. なお,\ k<0,\ 0 k1,\ 1

