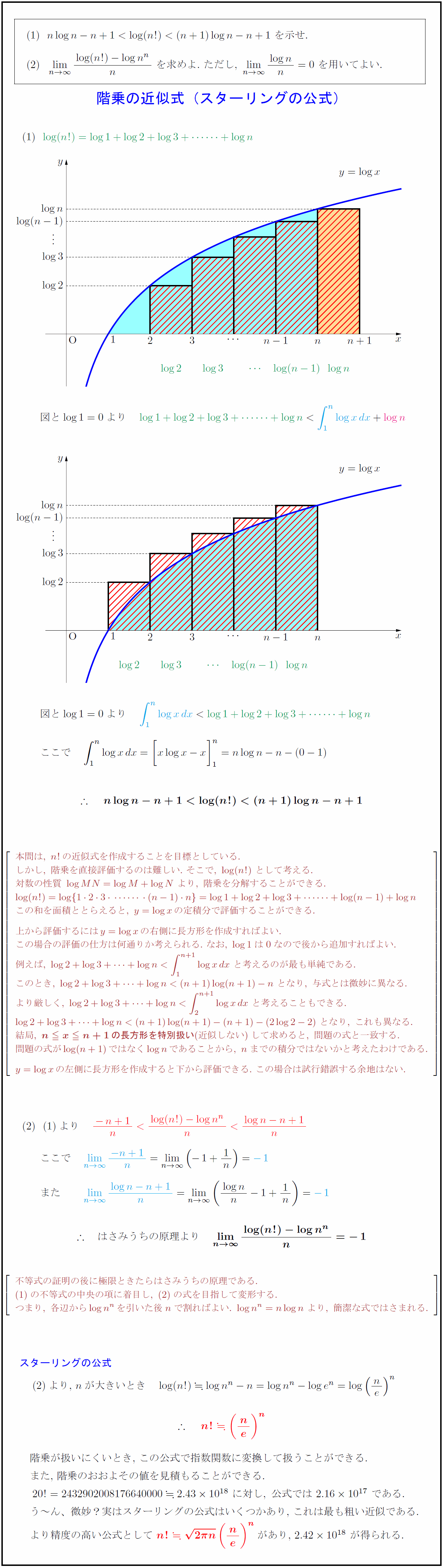
nlog n-n+1<log(n!)<(n+1)log n-n+1を示せ. 本問は,n!の近似式を作成することを目標としている. しかし,\ 階乗を直接評価するのは難しい.\ そこで,\ log(n!)\ として考える. 対数の性質\ log MN=log M+log N\ より,\ 階乗を分解することができる. この和を面積ととらえると,\ y=log xの定積分で評価することができる. 上から評価するにはy=log xの右側に長方形を作成すればよい. この場合の評価の仕方は何通りか考えられる.\ なお,\ log1は0なので後から追加すればよい. 例えば,\ log2+log3++log n<∫1}{n+1}log xdx\ と考えるのが最も単純である. このとき,\ log2+log3++log n<(n+1)log(n+1)-n\ となり,\ 与式とは微妙に異なる. より厳しく,\ log2+log3++log n<∫2}{n+1}log xdx\ と考えることもできる. log2+log3++log n<(n+1)log(n+1)-(n+1)-(2log2-2)\ となり,\ これも異なる. 結局,\ {n x n+1の長方形を特別扱い}(近似しない)して求めると,\ 問題の式と一致する. 問題の式がlog(n+1)ではなくlog nであることから,\ nまでの積分ではないかと考えたわけである. y=log xの左側に長方形を作成すると下から評価できる.\ この場合は試行錯誤する余地はない. 不等式の証明の後に極限ときたらはさみうちの原理である. の不等式の中央の項に着目し,\ の式を目指して変形する. つまり,\ 各辺からlog n^nを引いた後nで割ればよい.\ log n^n=nlog n\ より,\ 簡潔な式ではさまれる. }]$ スターリングの公式 階乗が扱いにくいとき,\ この公式で指数関数に変換して扱うことができる. また,\ 階乗のおおよその値を見積もることができる. に対し,\ 公式では\ 2.1610^{17}$\ である. う~ん、微妙?実はスターリングの公式はいくつかあり,\ これは最も粗い近似である. より精度の高い公式としてn!{2π n}( ne)^nがあり,\ 2.4210^{18} が得られる.

