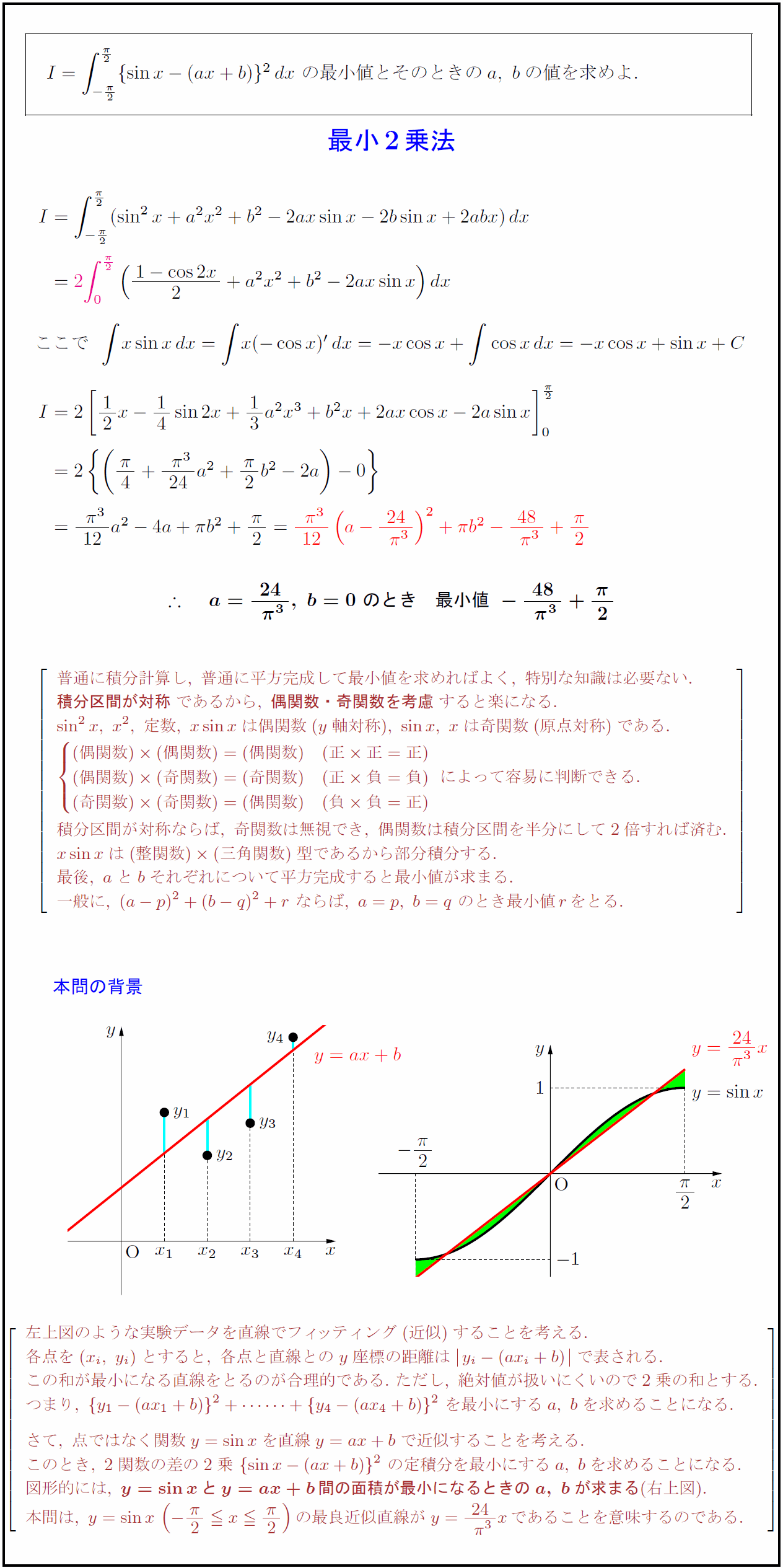
普通に積分計算し,\ 普通に平方完成して最小値を求めればよく,\ 特別な知識は必要ない. {積分区間が対称}であるから,\ {偶関数・奇関数を考慮}すると楽になる. sin²x,\ x²,\ 定数,\ xsin xは偶関数(y軸対称),\ sin x,\ xは奇関数(原点対称)である. (偶関数)(偶関数)=(偶関数) & (正 正=正) (偶関数)(奇関数)=(奇関数) & (正 負=負) (奇関数)(奇関数)=(偶関数) & (負 負=正) \ によって容易に判断できる. ₀ 積分区間が対称ならば,\ 奇関数は無視でき,\ 偶関数は積分区間を半分にして2倍すれば済む. xsin xは(整関数)(三角関数)型であるから部分積分する. 最後,\ aとbそれぞれについて平方完成すると最小値が求まる. 一般に,\ (a-p)²+(b-q)²+r\ ならば,\ a=p,\ b=q\ のとき最小値rをとる. 左上図のような実験データを直線でフィッティング(近似)することを考える.\ 各点を(x_i,\ y_i)とすると,\ 各点と直線とのy座標の距離はy_i-(ax_i+b)}で表される. この和が最小になる直線をとるのが合理的である.\ ただし,\ 絶対値が扱いにくいので2乗の和とする. つまり,\ {y₁-(ax₁+b)}²++{y₄-(ax₄+b)}²\ を最小にするa,\ bを求めることになる. さて,\ 点ではなく関数y=sin xを直線y=ax+bで近似することを考える. このとき,\ 2関数の差の2乗\ {sin x-(ax+b)}²\ の定積分を最小にするa,\ bを求めることになる. 図形的には,\ {y=sin xとy=ax+b間の面積が最小になるときのa,\ bが求まる}(右上図). 本問は,\ y=sin x(-{π}{2} x{π}{2})の最良近似直線がy={24}{\ π³}xであることを意味するのである.

