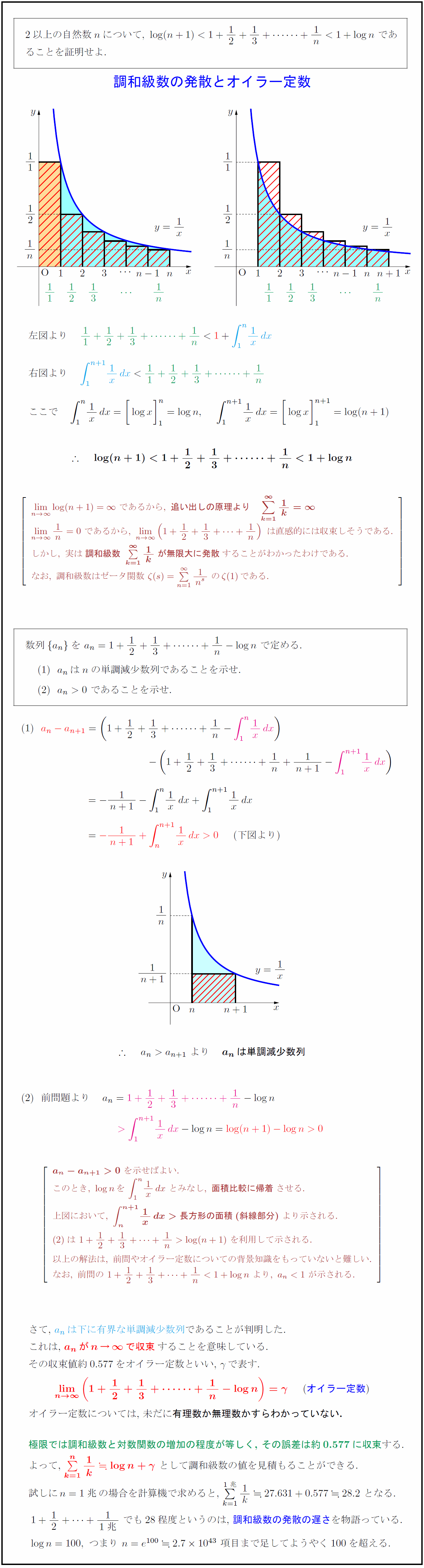
2以上の自然数nについて,\ log(n+1) lim[n→∞]log(n+1)=∞\ であるから,\ {追い出しの原理より は直感的には収束しそうである. しかし,\ 実は{調和級数\ Σ1k\ が無限大に発散}することがわかったわけである. なお,\ 調和級数はゼータ関数\ \zeta(s)=Σ{1}{n^s}\ の\zetaである.\ $a_nはnの単調減少数列であることを示せ.$ $a_n>0$\ であることを示せ. 単調減少数列}$} {a_n-a_{n+1}>0}\ を示せばよい. このとき,\ log nを\ ∫1}{n}1xdx\ とみなし,\ {面積比較に帰着}させる. 上図において,\ {∫n}{n+1}1xdx>長方形の面積(斜線部分)}\ より示される. 以上の解法は,\ 前問やオイラー定数についての背景知識をもっていないと難しい. なお,\ 前問の\ 1+12+13++1n<1+log n\ より,\ a_n<1\ が示される. さて,\ $a_n$は下に有界な単調減少数列}であることが判明した. これは,\ ${a_nがn→∞で収束}$}することを意味している. その収束値約0.577をオイラー定数といい,\ $γ$で表す. オイラー定数については,\ 未だに有理数か無理数かすらわかっていない.} 極限では調和級数と対数関数の増加の程度が等しく,\ その誤差は約0.577に収束する. よって,\ ${Σ{1}{k} log n+γ$\ として調和級数の値を見積もることができる. [-.2zh] 試しに$n=1兆$の場合を計算機で求めると,\ $1兆}{1}{k}27.631+0.57728.2$\ となる. $1+12++{1}{1兆}$\ でも28程度というのは,\ 調和級数の発散の遅さを物語っている. $log n=100,\ つまり\ n=e^{100}2.710^{43}$ 項目まで足してようやく100を超える.

