「e」は微分分野で学習しますので、初めて見る学生のために軽く説明しておきます。
eは「自然対数の底」と呼ばれる定数で、e≒2.718・・・です。
通常、対数では底eが省略されます。つまり、logxはlogexを意味しています。
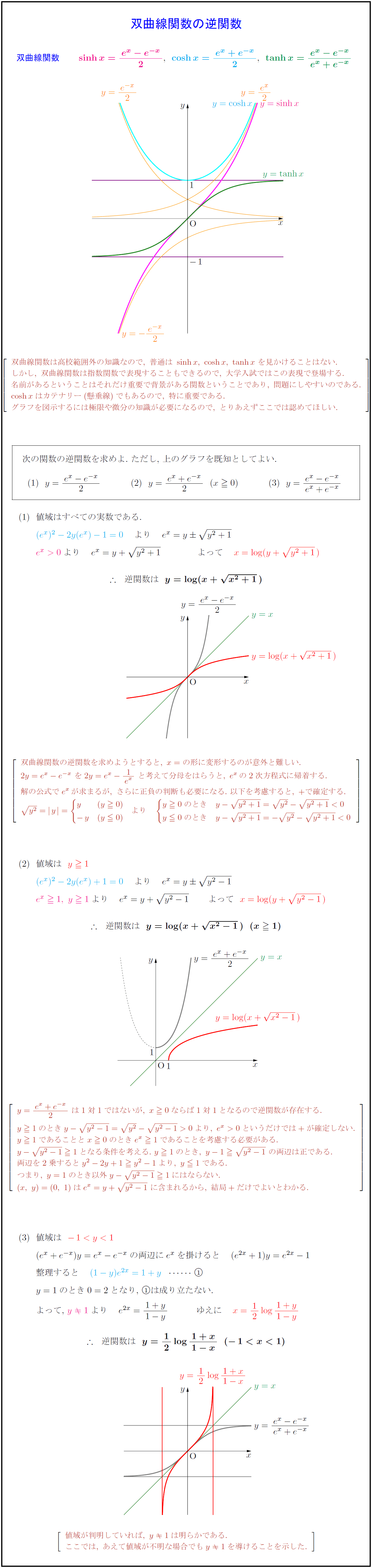
双曲線関数は高校範囲外の知識なので,\ 普通は\ sinh x,\ cosh x,\ tanh x\ を見かけることはない. しかし,\ 双曲線関数は指数関数で表現することもできるので,\ 大学入試ではこの表現で登場する. 名前があるということはそれだけ重要で背景がある関数ということであり,\ 問題にしやすいのである. cosh xはカテナリー(懸垂線)でもあるので,\ 特に重要である. グラフを図示するには極限や微分の知識が必要になるので,\ とりあえずここでは認めてほしい. }次の関数の逆関数を求めよ.\ ただし,\ 上のグラフを既知としてよい. 値域はすべての実数である. 双曲線関数の逆関数を求めようとすると,\ x=の形に変形するのが意外と難しい. 2y=e^x-e^{-x}\ を2y=e^x-{1}{e^x}\ と考えて分母をはらうと,\ e^xの2次方程式に帰着する. 解の公式でe^xが求まるが,\ さらに正負の判断も必要になる.\ 以下を考慮すると,\ +で確定する. は1対1ではないが,\ x0ならば1対1となるので逆関数が存在する. y1のときy-{y²-1}={y²}-{y²-1}>0より,\ e^x>0というだけでは+が確定しない. y1であることとx0のときe^x1であることを考慮する必要がある. y-{y²-1}1となる条件を考える.\ y1のとき,\ y-1{y²-1}\ の両辺は正である. 両辺を2乗するとy²-2y+1 y²-1より,\ y1である. つまり,\ y=1のとき以外y-{y²-1}1にはならない. (x,\ y)=(0,\ 1)はe^x=y+{y²-1}\ に含まれるから,\ 結局+だけでよいとわかる. 値域は$-1

