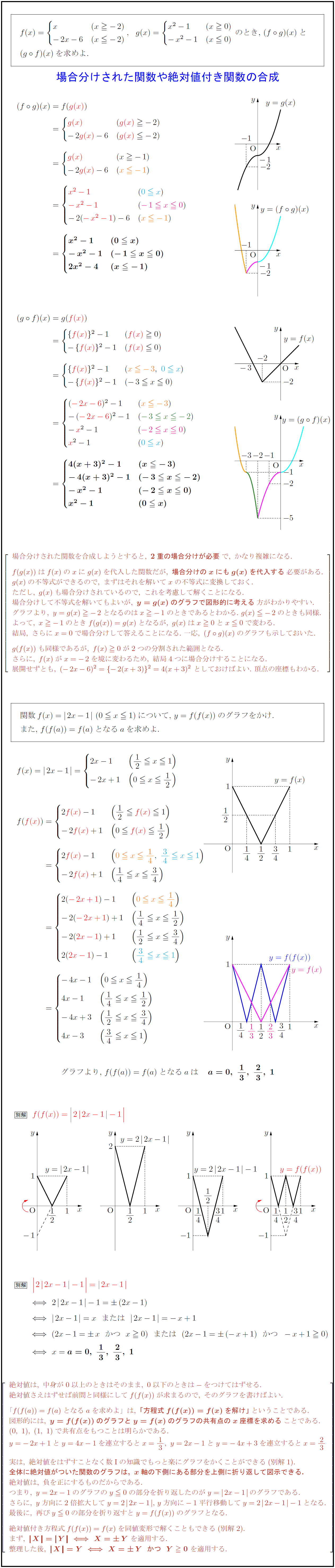
f(f(x))の場合分けで、0≦x≦1/4のとき-4x-1となっていますが、-4x+1の誤りですm(_ _)m
場合分けされた関数を合成しようとすると,\ {2重の場合分けが必要}で,\ かなり複雑になる. f(g(x))はf(x)のxにg(x)を代入した関数だが,\ {場合分けのxにもg(x)を代入する}必要がある. g(x)の不等式ができるので,\ まずはそれを解いてxの不等式に変換しておく. ただし,\ g(x)も場合分けされているので,\ これを考慮して解くことになる. 場合分けして不等式を解いてもよいが,\ {y=g(x)のグラフで図形的に考える}方がわかりやすい. グラフより,\ y=g(x)-2となるのはx-1のときであるとわかる.\ g(x)-2のときも同様. よって,\ x-1のときf(g(x))=g(x)となるが,\ g(x)はx0とx0で変わる. 結局,\ さらにx=0で場合分けして答えることになる.\ 一応,\ (f◦ g)(x)のグラフも示しておいた. g(f(x))も同様であるが,\ f(x)0が2つの分割された範囲となる. さらに,\ f(x)がx=-2を境に変わるため,\ 結局4つに場合分けすることになる. 展開せずとも,\ (-2x-6)²={-2(x+3)}²=4(x+3)²\ としておけばよい.\ 頂点の座標もわかる. 絶対値は,\ 中身が0以上のときはそのまま,\ 0以下のときは-をつけてはずせる. 絶対値さえはずせば前問と同様にしてf(f(x))が求まるので,\ そのグラフを書けばよい. 「f(f(a))=f(a)となるaを求めよ」は,\ {「方程式f(f(x))=f(x)を解け」}ということである. 図形的には,\ {y=f(f(x))のグラフとy=f(x)のグラフの共有点のx座標を求める}ことである. (0,\ 1),\ (1,\ 1)で共有点をもつことは明らかである. y=-2x+1とy=4x-1を連立するとx=13,\ y=2x-1とy=-4x+3を連立するとx=23 実は,\ 絶対値をはずすことなく数I}の知識でもっと楽にグラフをかくことができる(別解1). {全体に絶対値がついた関数のグラフは,\ x軸の下側にある部分を上側に折り返して図示できる.} 絶対値は,\ 負を正にするものだからである. つまり,\ y=2x-1のグラフのy0の部分を折り返したのがy=2x-1}のグラフである. さらに,\ y方向に2倍拡大してy=22x-1},y方向に-1平行移動してy=22x-1}-1となる. 最後に,\ 再びy0の部分を折り返すとy=f(f(x))のグラフとなる. 絶対値付き方程式f(f(x))=f(x)を同値変形で解くこともできる(別解2). まず,\ { X= YX=Y}\ を適用する. 整理した後,\ { X=YX=YかつY0}\ を適用する.

