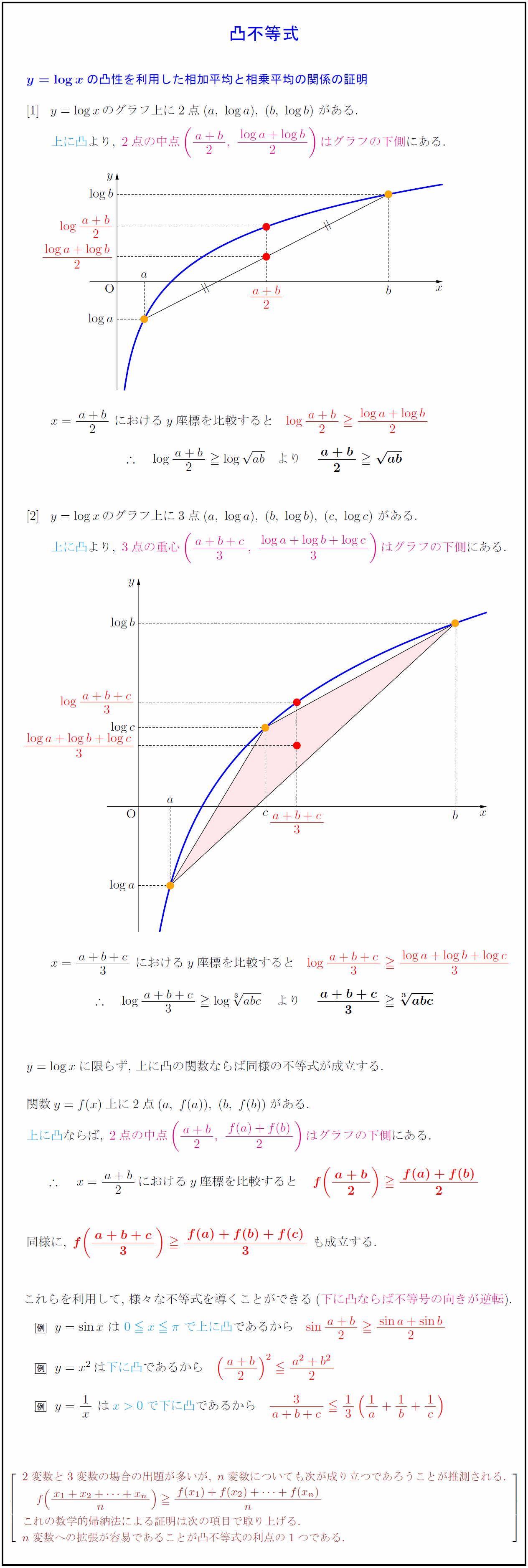
y=log xのグラフ上に2点(a,\ log a),\ (b,\ log b)\ がある.$ $y=log xのグラフ上に3点(a,\ log a),\ (b,\ log b),\ (c,\ log c)\ がある.$ $y=log x$に限らず,\ 上に凸の関数ならば同様の不等式が成立する. $関数y=f(x)上に2点(a,\ f(a)),\ (b,\ f(b))がある.$ $上に凸}ならば,\ 2点の中点({a+b}{2},\ {f(a)+f(b)}{2})はグラフの下側}にある.$ $ x={a+b}{2}におけるy座標を比較すると これらを利用して,\ 様々な不等式を導くことができる(下に凸ならば不等号の向きが逆転}). $y=sin x\ は\ 0 xπ\ で上に凸}であるから sin{a+b}{2}{sin a+sin b}{2$ 2変数と3変数の場合の出題が多いが,\ n変数についても次が成り立つであろうことが推測される. f({x₁+x₂++x_n}{n}){f(x₁)+f(x₂)++f(x_n)}{n} これの数学的帰納法による証明は次の項目で取り上げる. n変数への拡張が容易であることが凸不等式の利点の1つである.

