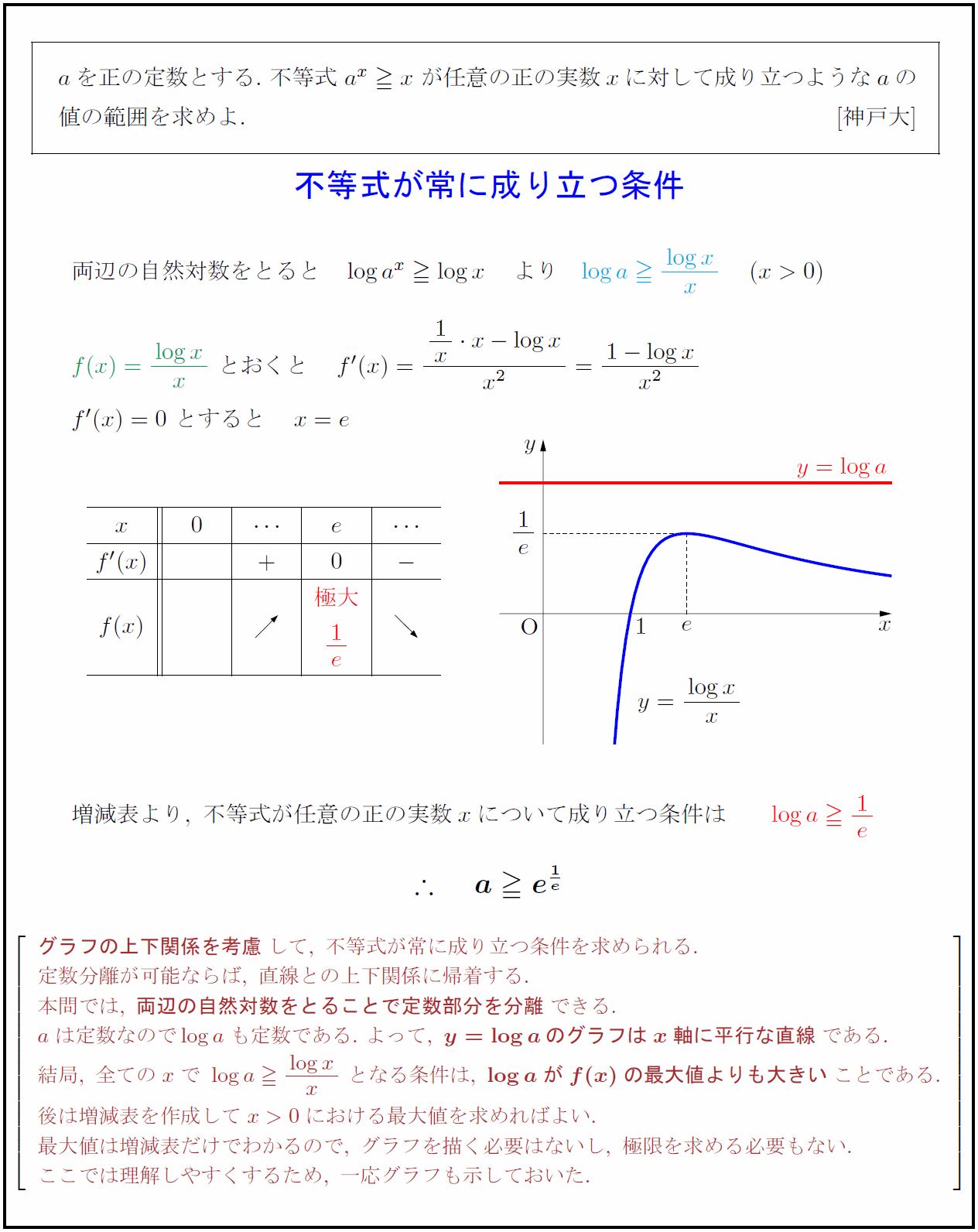
aを正の定数とする.\ 不等式\ a^x x\ が任意の正の実数xに対して成り立つようなaの$ $値の範囲を求めよ. \ [神戸大]$ $増減表より,\ 不等式が任意の正の実数xについて成り立つ条件は {グラフの上下関係を考慮}して,\ 不等式が常に成り立つ条件を求められる. 定数分離が可能ならば,\ 直線との上下関係に帰着する. 本問では,\ {両辺の自然対数をとることで定数部分を分離}できる. aは定数なのでlog aも定数である.\ よって,\ {y=log aのグラフはx軸に平行な直線}である. 結局,\ 全てのxで\ log a{log x}{x}\ となる条件は,\ {log aがf(x)の最大値よりも大きい}ことである. 後は増減表を作成してx>0における最大値を求めればよい. 最大値は増減表だけでわかるので,\ グラフを描く必要はないし,\ 極限を求める必要もない. ここでは理解しやすくするため,\ 一応グラフも示しておいた.

