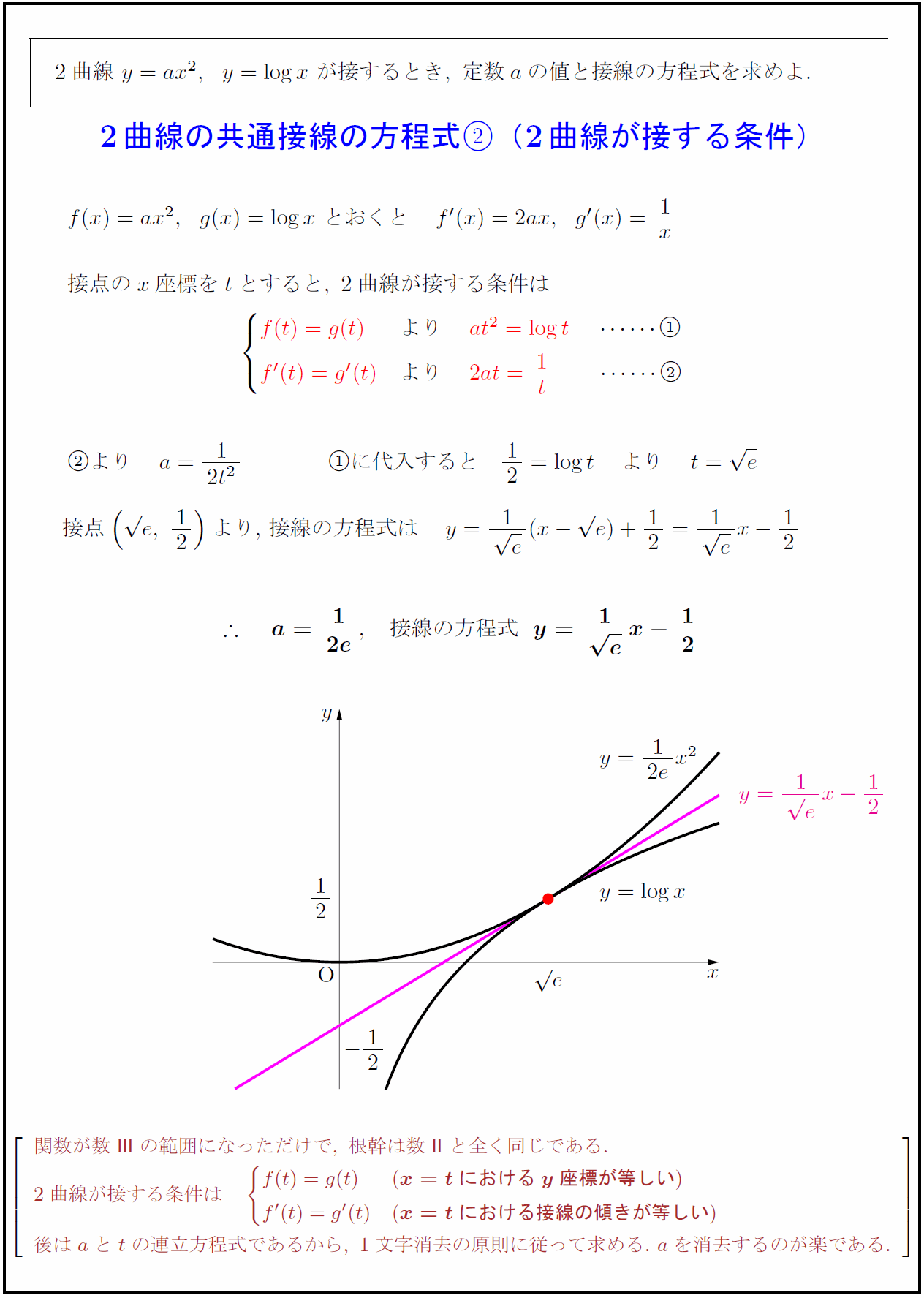
2曲線\ y=ax²,y=log x\ が接するとき,\ 定数aの値と接線の方程式を求めよ.$ { 2曲線の共通接線の方程式(2曲線が接する条件) $f(x)=ax²,g(x)=log x\ とおくと f'(x)=2ax,g'(x)=1x$ $接点のx座標をtとすると,\ 2曲線が接する条件は$ に代入すると 12=log t より t= e$ 接点$( e,\ 12)$より,\ 接線の方程式は $y={1}{ e}(x- e)+12={1}{ e}x-12$ $ {a={1}{2e, 接線の方程式{y={1}{ e}x-12}$} 関数が数III}の範囲になっただけで,\ 根幹は数II}と全く同じである. 2曲線が接する条件は f(t)=g(t) & ({x=tにおけるy座標が等しい}) f'(t)=g'(t) & ({x=tにおける接線の傾きが等しい}) ₀ 後はaとtの連立方程式であるから,\ 1文字消去の原則に従って求める.\ aを消去するのが楽である.

