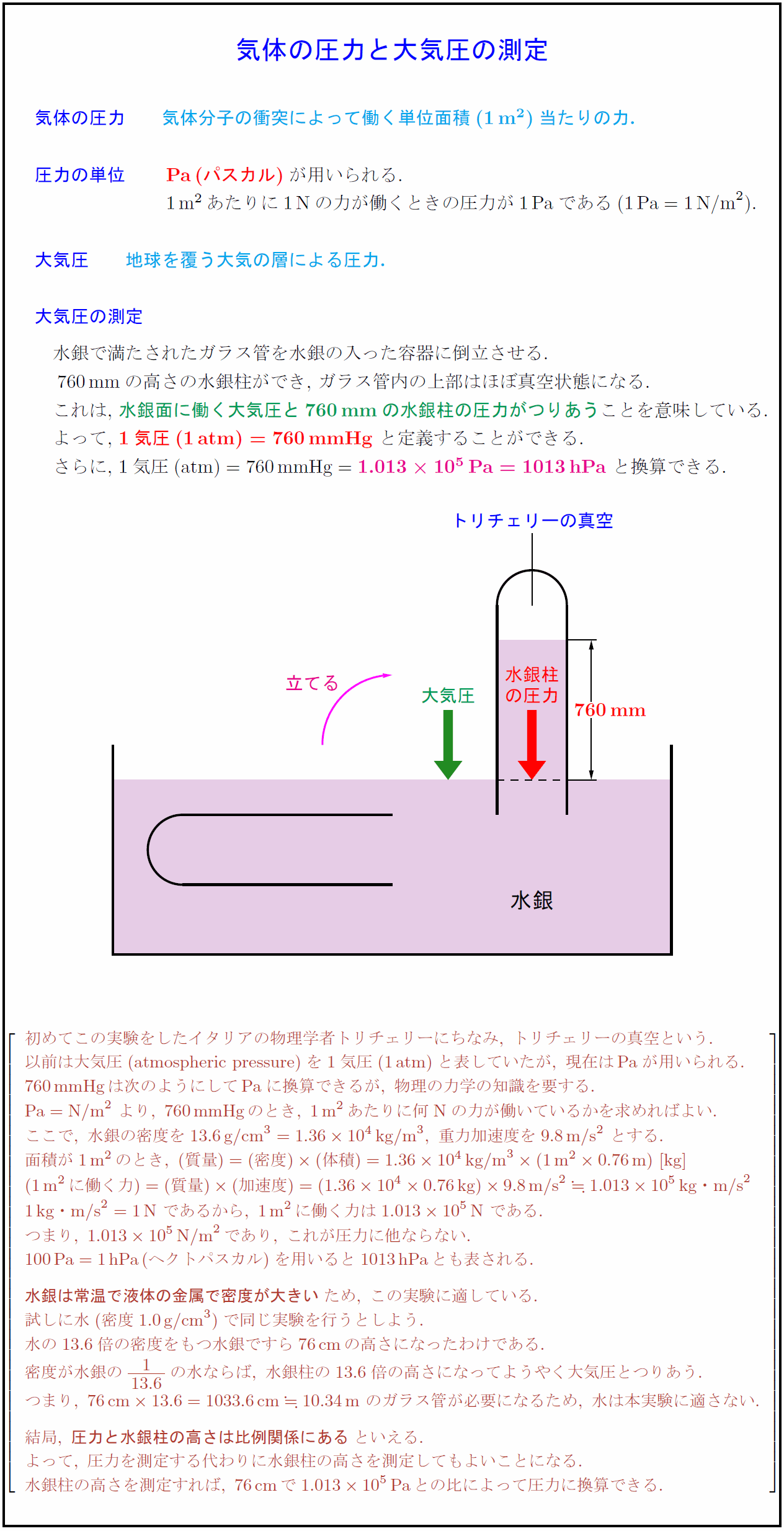
気体の圧力気体分子の衝突によって働く単位面積当たりの力. 圧力の単位 Pa(パスカル)が用いられる. 1m$²$あたりに1Nの力が働くときの圧力が1Paである($1Pa}=1N/m}²$). 大気圧 地球を覆う大気の層による圧力. {大気圧の測定 水銀で満たされたガラス管を水銀の入った容器に倒立させる. 760mmの高さの水銀柱ができ,\ ガラス管内の上部はほぼ真空状態になる. これは,\ 水銀面に働く大気圧と760mmの水銀柱の圧力がつりあうことを意味している. よって,\ 1気圧(1atm)=760}$mmHg\ と定義することができる. さらに,\ $1気圧(atm})=760mmHg}={1.01310⁵Pa=1013hPa$\ と換算できる.トリチェリーの真空大気圧水銀柱 初めてこの実験をしたイタリアの物理学者トリチェリーにちなみ,\ トリチェリーの真空という. 以前は大気圧(atmospheric pressure})を1気圧(1atm})と表していたが,\ 現在はPa}が用いられる. 760mmHg}は次のようにしてPa}に換算できるが,\ 物理の力学の知識を要する. Pa}=N/m}²\ より,\ 760mmHg}のとき,\ 1m}²あたりに何N}の力が働いているかを求めればよい. ここで,\ 水銀の密度を13.6g/cm³=1.3610⁴kg/m³,\ 重力加速度を9.8m/s}²\ とする. 面積が1m}²のとき,\ (質量)=(密度)(体積)=1.3610⁴kg/m³(1m}²0.76m})\ [kg}] (1m}²に働く力)=(質量)(加速度)= 1kg・m/s}²=1N}\ であるから,\ 1m}²に働く力は1.01310⁵N}\ である. つまり,\ 1.01310⁵N/m}²であり,\ これが圧力に他ならない. 100Pa}=1hPa}(ヘクトパスカル)を用いると1013hPa}とも表される. {水銀は常温で液体の金属で密度が大きい}ため,\ この実験に適している. 試しに水(密度1.0g/cm³)で同じ実験を行うとしよう. 水の13.6倍の密度をもつ水銀ですら76cm}の高さになったわけである. 密度が水銀の{1}{13.6}の水ならば,\ 水銀柱の13.6倍の高さになってようやく大気圧とつりあう. つまり,\ 76cm}13.6=1033.6cm}10.34m}\ のガラス管が必要になるため,\ 水は本実験に適さない. 結局,\ {圧力と水銀柱の高さは比例関係にある}といえる. よって,\ 圧力を測定する代わりに水銀柱の高さを測定してもよいことになる. 水銀柱の高さを測定すれば,\ 76cm}で1.01310⁵Pa}との比によって圧力に換算できる.

