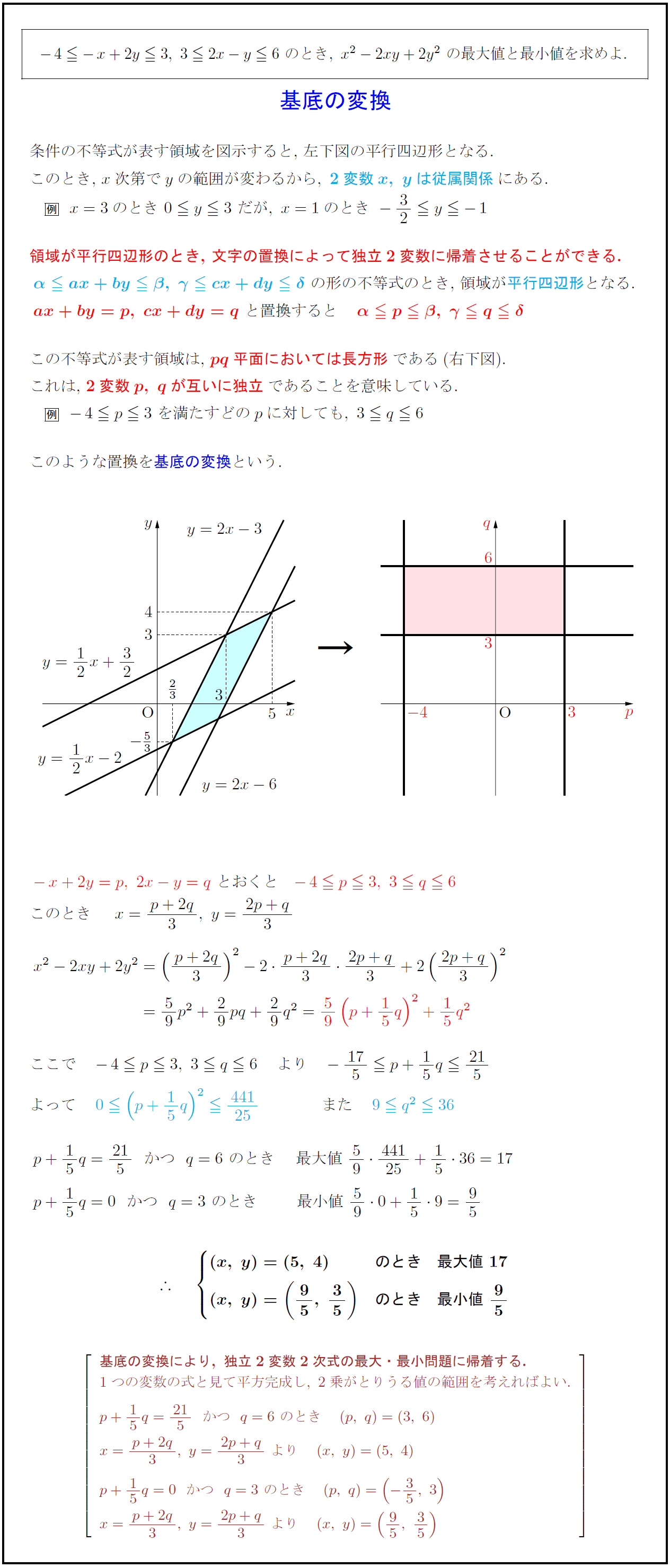
条件の不等式が表す領域を図示すると,\ 左下図となる. このとき,\ $x次第でyの範囲が変わるから,\ {2変数x,\ yは従属関係にある.$ { $x=3のとき\ 0 y3\ だが,\ x=1のとき\ -32 y-1$} 領域が平行四辺形のとき,\ 文字の置換により,\ 独立2変数に帰着できる.領域が平行四辺形となる. ${ax+by=p,\ cx+dy=q\ と置換する この不等式が表す領域は,\ ${pq平面においては長方形である(右下図).$ これは,\ ${2変数p,\ qが互いに独立であることを意味している. このような置換を基底の変換という. {基底の変換により,\ 独立2変数2次式の最大・最小問題に帰着する.} 1つの変数の式と見て平方完成して,\ 2乗がとりうる値の範囲を考えればよい.

