
連続型確率変数Xの確率密度関数$f(x)$が$f(x)=1} Xは正規分布$N(m,\ σ^2)}$に従うといい,\ $y=f(x)$のグラフを正規分布曲線という.確率変数Xが正規分布N(m,\ σ^2)に従う$とき
$平均}\ \ E(X)=m}, 標準偏差}\ \ 正規分布曲線の性質
[1]\ \ 確率密度関数なので$常にf(x)≧0$かつ$(全面積)=1$ 直線$x=m}$\,(平均)に関して対称であり,\ $x=m}$で最大値をとる.
[3]\ \ $x=m$から遠ざかるにつれて限りなく0に近づく($x$軸が漸近線).\ \ 0にはならない.
[4]\ \ σが大きくなるほど山が低く横に広くなり,\ 小さくなるほど$x=m$の周りに集中する.
Nは正規分布(Normal distribution})の頭文字である.
自然対数の底eは無理数で,\ e=2.718・・・\,(定数)である(数III}).
正規分布曲線の式を覚える必要はない.\ 概形と性質を覚えておく.
[4]\ \ 標準偏差\,σ\,は,\ 平均値周りの散らばり}を意味するのであった.
\ \ 全面積は常に1であるから,\ 標準偏差\,σ\,が大きくなるにつれて山の高さは低くなる.
[5]\ \ Xが正規分布に従うとき,\ 各区間におさまる確率が約68,\ 95,\ 99\%になることは覚えておきたい.
\ \ ちなみに,\ 平均が50,\ 標準偏差が10になるように調整した値がいわゆる偏差値である.
\ \ 例えば,\ 1万人の試験結果が正規分布に従うとすると,\ 偏差値40~60の人は約6827人いる.
\ \ また,\ 対称性より,\ 偏差値80以上の人は約(10000-9973)÷2=13.5人いる.
正規分布曲線の関数としての本質はy=e^{-x^2}\,であり,\ 数III}を学ぶと自力で図示できるようになる.
また,\ x=m±σ\,で変曲点(上に凸と下に凸が入れ替わる点)をとることもわかる.
標準正規分布
確率変数$X}$が正規分布$N(m,\ σ^2)}$に従うとき,\ $Z=X-m}{σ$とおくと,
確率変数$Z}$は標準正規分布$N(0,\ 1)}$に従う(平均0,\ 標準偏差1になる).
正規分布を標準正規分布に変換することを標準化という.
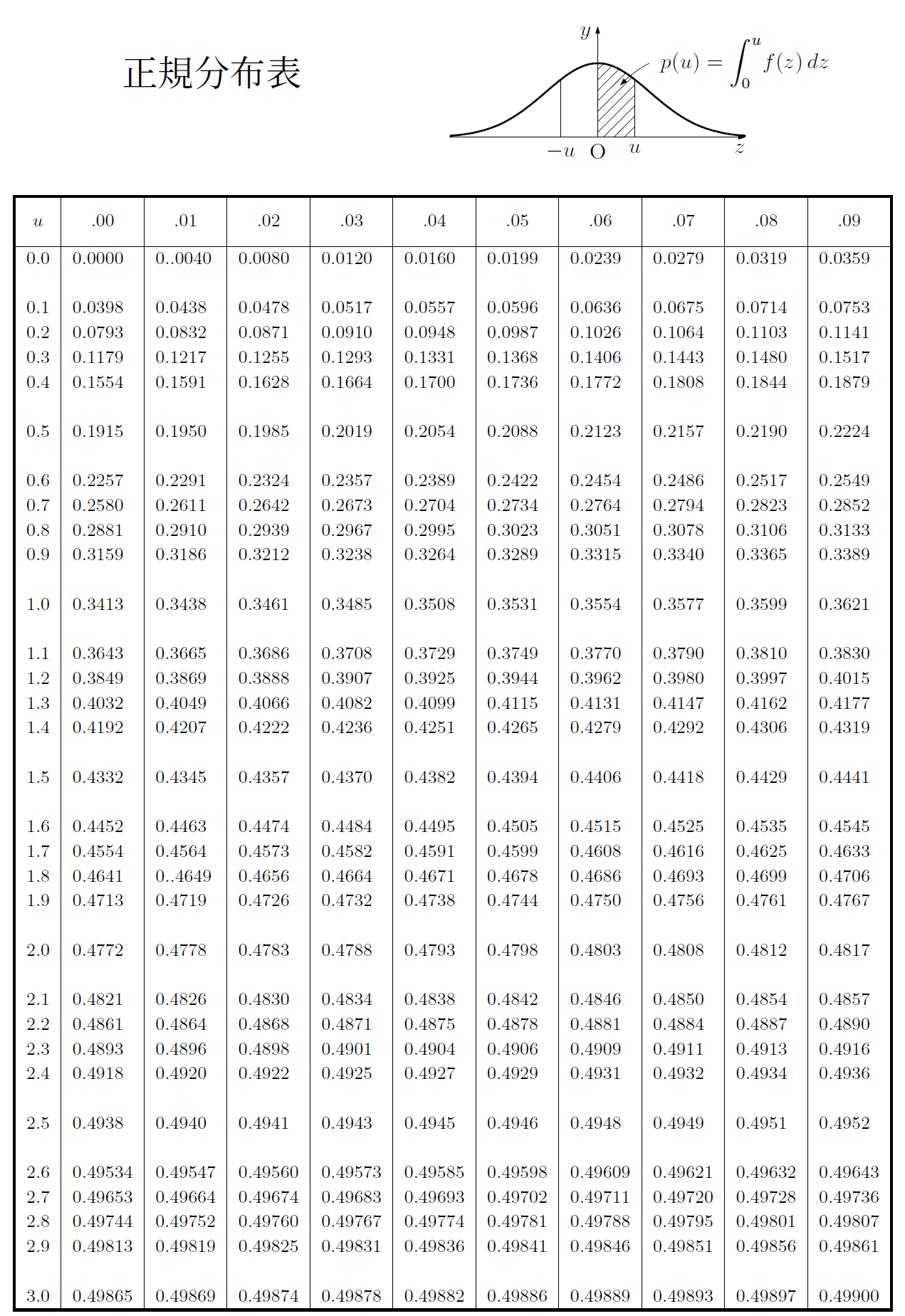
様々な$u$の値に対する$p(u)$の近似値を表にまとめたものを正規分布表という.
証明もできるようにしておくこと.
連続型確率変数の変換公式E(aX+b)=aE(X)+b,\ V(aX+b)=a^2\,V(X)}を利用する.
正規分布表と呼ばれることが多いが,\ 正確には\dot{標}\dot{準}正規分布の表である.
一般に,\ Xが正規分布に従うとき,\ aX+bも正規分布に従う}ことが知られている.
つまり,\ すべての正規分布は,\ 標準化して標準正規分布に変換でき,\ 標準正規分布表を利用できる.}
確率変数Xが正規分布$N(10,\ 4^2)$に従うとき,\ 次の確率を求めよ.
正規分布は,\ とにかく標準化して正規分布表を利用する.
正規分布表には,\ uの一の位と小数第1位が左端の列,\ uの小数第2位が一番上の行に示されている.
例えば,\ u=1.24ならば,\ 左端1.2,\ 最上行.04のマスを読み,\ p(1.24)=0.3925とわかる.
(1)\ \ 正規分布表の値は,\ いずれも左端が0の区間0≦ Z≦ uにおさまる確率}である.
\ \ 左端が0でない区間の確率は,\ 差に分解するなどの工夫をして求めることになる.
\ \ 面積でとらえておくことも重要である.\ 求めるのは,\ 図の色塗り部分の面積である.
\ \ 標準正規分布は平均が0なので,\ その確率密度関数y=f(z)はy軸対称のグラフ}となる.
\ \ 結局,\ ∫{0.5}{2}=∫{0}{2}-∫{0}{0.5}ということである.
(2)\ \ -∞≦ z≦-\,1における面積を求めることになる.
\ \ このように,\ 区間が±∞\,や0以下にまで及ぶ場合,\ グラフの対称性を利用}する必要がある.
\ \ まず,\ 対称性により,\ -\,∞≦ z≦-\,1における面積は1≦ z≦∞\,における面積に等しい.
\ \ さらに,\ 全面積1}より,\ 0≦ z≦∞\,における面積P(Z≧0)が0.5}であることも利用する.
ある大学の入試で,\ 募集80人に対して400人が受験した.\ 試験は500点満点で,\ その
得点分布は平均点315点,\ 標準偏差40点の正規分布とみなせた.
(1)\ \ 305点の人の順位は約何番か.
(2)\ \ 合格最低点は約何点か. \\
点数をXとすると,\ Xは正規分布$N(315,\ 40^2)$に従う.
よって,\ $Z=X-315}{40}$}とおくと,\ $Z$は標準正規分布$N(0,\ 1)$に従う.
∴\ \ $$400×0.5987=239.48$より,\ 305点の人は約239番}である.} \\
(2)\ \ 合格最低点を$A$とする.
(1)\ \ 301点の人が上から約何割の位置にいるか(301点以上の人の割合)を求めればよい.
(2)\ \ 逆に,\ 上から0.2の割合の位置にいる人の点数を求めることになる.
\ \ 結局,\ p(u)=0.3となればよく,\

