
特性Aの母比率$p}$\ \, 母集団の中である特性Aをもつ要素の割合.
特性Aの標本比率$R}$ 標本の中である特性Aをもつ要素の割合.
母比率$p}$の母集団から大きさ$n}$の無作為標本を抽出したときの標本比率$R}$の分布}を考える.
標本の中で特性Aをもつ要素の個数を確率変数Xとすると $R=X}{n}$
復元抽出ならば$P(X=k)=C nkp^k(1-p)^{n-k}$であり,\ Xは二項分布$B(n,\ p)$に従う.}
よって,\ $n$が大きいとき},\ Xは近似的に正規分布$N(np,\ np(1-p))$に従う.}
ここで,\ Xは二項分布$B(n,\ p)$に従うから,\ 標本比率$R$の期待値$E(R)$と標準偏差$σ(R)$は
結局,\ $n}$が大きいとき,\ 標本比率$R= Xn}$は近似的に正規分布$N-.2zw}p,\ p(1-p)}{n$に従う.
$\left[l}
最初の設定以外はほとんど既習事項の復習である.
標本調査では,\ 母集団が十分に大きく,\ 標本は復元抽出(反復試行)で作ると考えてよい.
1回の試行で事象Aの起こる確率がpの試行をn回行うとする(反復試行).
このとき,\ 事象Aの起こる回数Xは二項分布B(n,\ p)に従うのであった.
Xが二項分布B(n,\ p)に従うとき,\ 平均E(X)=np,\ 分散V(X)=npq\ (q=1-p)}であった.
ここで,\ 平均E(X)=m,\ 標準偏差\,σ(X)=σ\,であるような正規分布をN(m,\ σ^2)と表すのであった.
nが大きいとき},\ 二項分布B(n,\ p)は同じ平均と分散をもつ正規分布N(np,\ npq)で近似できた.}
さらに,\ 公式E(aX)=aE(X),\ V(aX)=a^2V(X)}を用いて,\ E(R)とσ(R)を求められる.
また,\ Xが正規分布に従うとき,\ aX+bも正規分布に従うことが知られている.
よって,\ Rは近似的に平均E(R)=p,\ 標準偏差\,σ(R)=√{p(1-p)}{n\,の正規分布に従う.
母比率がpのとき,\ 標本比率の期待値(平均)もpになることは直感的にも納得できる.
また,\ nが大きくなるほど標準偏差(平均値周りの散らばり)は小さくなる.
参考までに,\ 標本比率の分布についての別の観点を紹介しておく.
特性 Aの母比率pの母集団の各要素に対して,\ 次のようなダミー変量Xを設定する.
このようなダミー変量は,\ 個数や回数の期待値を求めるときにも利用できた(数 A:確率).
例えば,\ 大きさ3の標本を抽出したとき,\ 1回目と3回目の要素が特性 Aをもっていたとしよう.
このとき,\ 標本の中で特性 Aをもつ要素の個数をX_1+X_2+X_3=1+0+1=2個と求められる.
大きさnの標本に一般化すると,\ 標本の中で特性 Aをもつ要素の個数は X_1+X_2+・・・+X_n
このとき,\ 標本比率R=X_1+X_2+・・・+X_n}{n}= X\,となる.
結局,\ 標本比率Rは標本平均の一種}であり,\ 標本平均と同様に近似的に正規分布に従う.
10万本の当たりくじを含む100万本のくじの中から$n$本引いたときの当たりくじの
割合を$R$とする.
(1)\ \ $n=100$のとき,\ 標本比率$R$の期待値$E(R)$と標準偏差$σ(R)$を求めよ.
(2)\ \ $n=100$のとき,\ 16本以上の当たりくじを引く確率を求めよ.
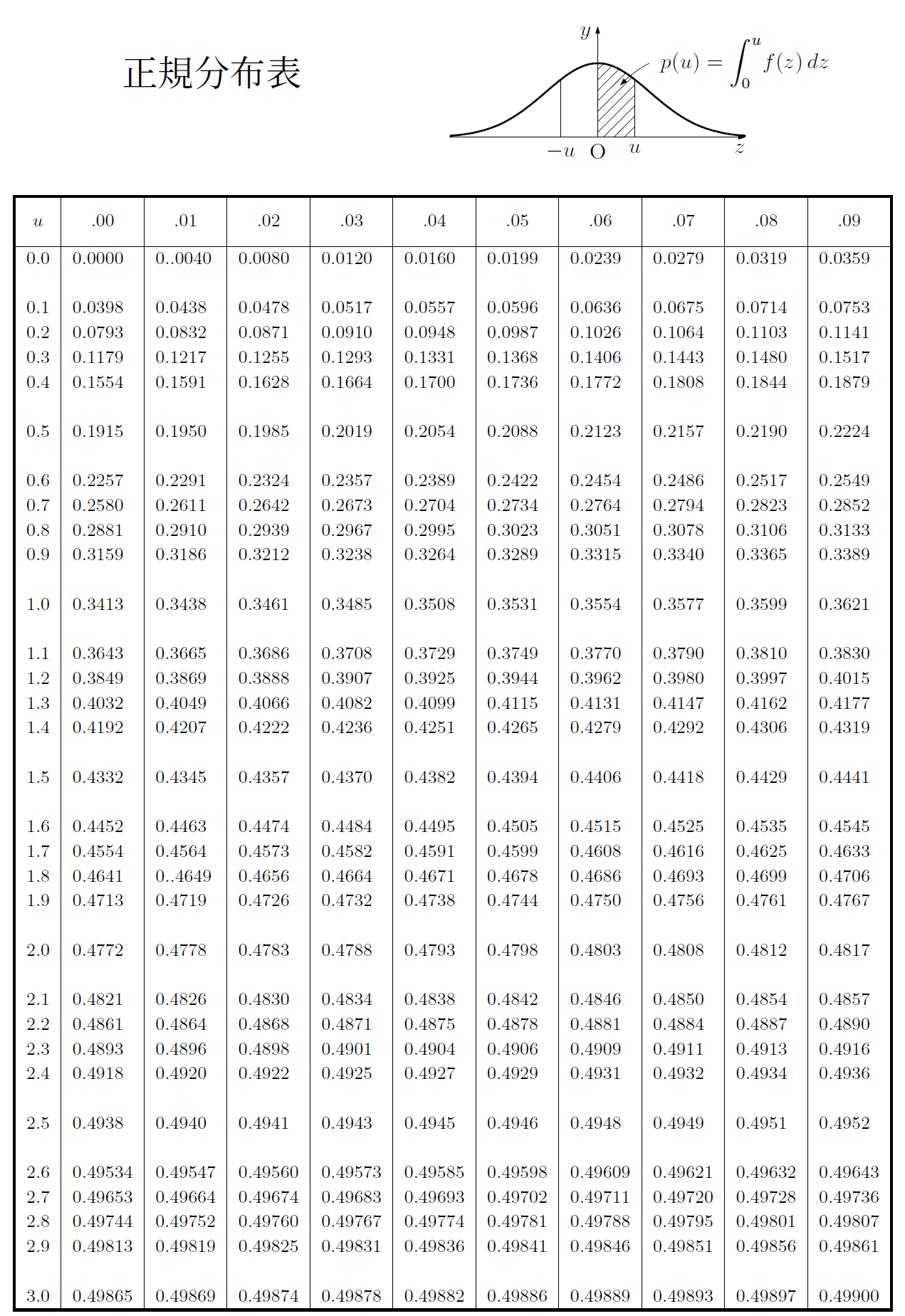
例によって,\ 正規分布は標準正規分布に変換し,\ 正規分布表を利用する.}
Xが平均m,\ 標準偏差\,σ\,の正規分布N(m,\ σ^2)に従うとする.
このとき,\ Z=X-m}{σ\,とおくと,\ Zは標準正規分布N(0,\ 1)に従うのであった.
すでに本問と本質的に同じ問題を「二項分布の正規分布による近似」の項で扱った.
ここでは,\ その復習に加えて改めて問題の意味合いと背景を確認する.
実際にくじをn本引いたときの当たりくじの割合Rは統計的確率}である.
仮に900本のくじ引いて当たりくじが92本だったならば,\ R=92}{900}≒0.102となる.
一方,\ 当たりくじを引く数学的確率}(理論値)は当然\,1}{10}=0.1\ (母比率})である.
R-1}{10\,は統計的確率と数学的確率の誤差}を意味しており,\ この場合の誤差は約0.002となる.
ここで,\ 実際に100万本のくじの中から900本のくじを引くことを何回も繰り返すとしよう.
900本の内の当たりくじの本数は毎回変わるから,\ 統計的確率も誤差も毎回変わる.
このときの誤差が0.01以下におさまる確率を求めるのが本問である.
標本平均\, X\,は,\ nが大きくなるほど母平均mに近い値をとりやすくなるのであった(大数の法則).
標本比率も標本平均の一種であるから,\ これを以下のように言い換えることができる.
標本比率Rは,\ nが大きくなるほど母比率pに近い値をとりやすくなる(大数の法則).}
本問はこれの確認であり,\ 実際n=3600の場合の方が誤差が0.01以下になる確率が高い.
大数の法則は,\ 標本比率から逆に母比率が推定できることを示唆している.

