
確率変数Xが$二項分布B(n,\ p)に従う}$とする.
$X=r$となる確率を$P_r$とすると $P_r=C nrp^r(1-p)^{n-r}$
試しに,\ $p=16$のとき,\ $n=10,\ 30,\ 50$の各場合について計算し,
点$(r,\ P_r)$をとって折れ線グラフで表してみると以下となる. \\
二項分布のグラフは,\ $n}$が大きくなるとほぼ左右対称となり,\ 正規分布曲線に近づく.
一般に,\ 次の定理が知られている(証明は高校範囲外).
二項分布$B(n,\ p)}$に従う確率変数であるとする.
$Xは,\ nが大きいとき,\ 近似的に正規分布N(np,\ npq)\ (q=1-p)に従う.$
よって,\ $Z=X-np}{√{npq$は,\ 近似的に標準正規分布$N(0,\ 1)}$に従う.
1回の試行で事象Aが起こる確率がpの試行をn回行う(反復試行).
事象Aの起こる回数をXとするとき,\ 確率変数Xは二項分布B(n,\ p)に従うのであった.
上表は,\ サイコロを10,\ 30,\ 50回振って1の目がr回出る確率P_r\,の折れ線グラフと考えられる.
確率変数Xが二項分布B(n,\ p)に従うとき,\ 平均E(X)=np,\ 分散V(X)=npq}であった.
また,\ 平均m,\ 分散\,σ^2\,(標準偏差\,σ)であるような正規分布をN(m,\ σ^2)と表すのであった.
$結局,\ nが大きいとき,\ 二項分布B(n,\ p)は同じ平均と分散をもつ正規分布N(np,\ npq)で近似できる.}$
さらに,\ 正規分布は,\ Z=X-m}{σ\,とおくことで標準正規分布(平均0,\ 分散1)に変換できた.
このようにして,\ 離散型確率変数を連続型確率変数として扱い,\ 正規分布表が利用できるようになる.
元はといえば,\ 正規分布は二項分布のnを大きくして発見されたものである.
実用上は,\ np>5かつnq>5,\ つまりn×(p,\ qの小さい方)>5であれば近似してよいとされる.
サイコロ180個を同時に振るとき,\ 1の目が出るサイコロの個数をXとする.
このとき,\ $20≦ X≦35$となる確率$P(20≦ X≦35)$を求めよ. \\
Xは二項分布$B-.2zw}180,\ 16$に従う.}
Xの平均は$m}=np=180・16=30}$,\ \ 標準偏差は$σ}=√{npq}=√{180・16・56}=5}$
180個は十分大きいから,\ Xは近似的に正規分布$N(30,\ 5^2)$に従う.}
よって,\ $Z=X-30}{5$とおくと,\ $Z$は近似的に標準正規分布$N(0,\ 1)$に従う.
1個のサイコロを180回振ることと,\ サイコロ180個を同時に振ることは同じであった(反復試行).
np=30>5より正規分布で近似し,\ 標準正規分布に変換して正規分布表を利用する.
本問を近似せずに求めようとすると次を計算する羽目になることからも近似の有用性がわかる.
さて,\ 計算機で真の確率を求めてみると約0.8494となるので,\ 近似で3\%ほどの誤差が生じている.
誤差をどの程度許容するかは目的によって変わるとはいえ,\ 3\%は大きいと感じるかもしれない.
実は,\ 半整数補正}という簡単に近似精度を高くする方法がある.
離散型確率変数Xを連続型確率変数Yで近似する際に上端と下端を\,12\,ずつ広くする}のである. \ 誤差が0.3\%にまで小さくなり,\ これならば許容範囲だと感じる人が多いだろう.
一般に,\ nが大きくpが\,12\,に近いほどnpとnqが大きくなり,\ 近似精度が高くなる.
本来,\ 高い精度の近似を得るには,\ かなりnが大きくなければならない.
しかし,\ 半整数補正を行うと,\ npとnqが5程度でも実用上十分な精度で近似できるのである.
以下,\ 半整数補正で近似精度が高くなる理由を説明しておく.
二項分布B-.2zw}180,\ 16のヒストグラムを正確に図示すると下図となる.
よって,\ P(20≦ X≦35)は下図の緑斜線部分の面積に等しい.
解答ではこれをm=30,\ σ=5の正規分布曲線y=f(x)で近似し,∫{20}{35}f(x)\,dx=0.8185と求めた.
∫{20}{35}f(x)\,dxで求まるのは下図の色塗り部分なのだが,\ 両端をよく見てほしい.
X=20とX=35のときの長方形の面積の約半分が除かれてしまっているではないか.
これでは真の値よりも小さくなるのは当然で,\ ∫{19.5}{35.5}f(x)\,dxとすると斜線部分の面積とほぼ一致する. サイコロ$n$個を同時に振るとき,\ 1の目が出るサイコロの個数をXとする.
$ Xn-16}≦0.01$となる確率が0.95以上になるような$n$の最小値を求めよ.二項分布$B-.2zw}n,\ 16$に従う.}
Xの平均は$m}=np= n6}$,\ \ 標準偏差は$σ}=√{npq}=√{n・16・56}=√{5n{6$
$n$が十分大きいとき,\ Xは近似的に正規分布$N-.2zw} n6,\ √{5n{6}^2$に従う.}
このとき,\ $Z=X- n6}{√{5n{6$とおくと,\ $Z$は近似的に標準正規分布$N(0,\ 1)$に従う. \\
先に本問の背景について解説する.
Xn\,は統計的確率}(実際に振ってみた結果から導かれる確率)である.
実際に600個のサイコロを同時に振って1の目が102個出たならば,\ Xn=102}{600}=0.17となる.
一方,\ 1の目が出る数学的確率}(理論値)は当然\,16=0.166・・・\,である.
Xn-16}\,は統計的確率と数学的確率の誤差}を意味しており,\ この場合の誤差は約0.003となる.
さて,\ 実際にサイコロn個を同時に振ることを繰り返すとしよう.
1の目が出るサイコロの個数Xは毎回変わるから,\ 統計的確率も誤差も毎回変わる.
100回繰り返して95回以上誤差が0.01以下におさまるようなnの最小値を求めるのが本問である.
数式的には,\ P-.2zw}\, Xn-16}≦0.01≧0.95を満たすnの最小値を求める問題である.
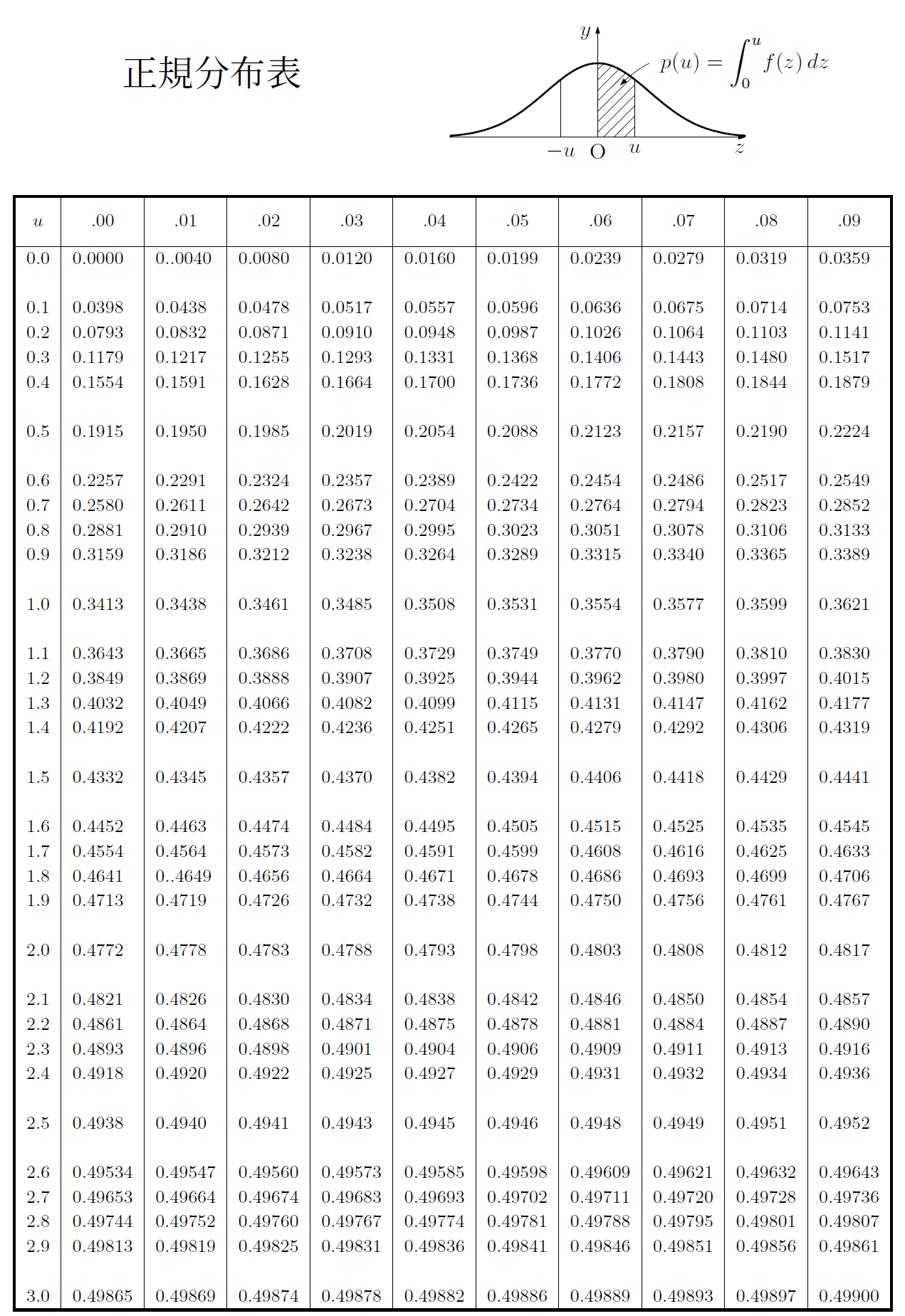
後は標準正規分布に変換して正規分布表を利用すればよい. p(1.96)=0.4750
本問の0.01を0.001にしたり0.95を0.99にしたりして計算してみると,\ nの最小値は大きくなる.
このことから,\ nの値が大きくなるほど誤差が小さくなる}ことがわかる.
もしnを大きくしても\,16\,との誤差が大きいままならば,\ サイコロの公平性が疑われる.
逆に,\ 数学的確率が不明ないびつなサイコロの場合,\ nを大きくすることで真の確率を推測できる.

