
母集団\{1,\ 2,\ 3\}から大きさ2の標本$\{X_1,\ X_2\}$を復元抽出する.
このとき,\ 標本平均$ X$の確率分布は左表になるのであった(前項参照).
左表を元に作成した標本平均$ X$の分布を表すヒストグラムが右表である.
一方,\ 大きさ8の標本を復元抽出するときの確率分布とヒストグラムは以下になる.
標本の大きさ$n=2$のとき,\ $ X$の分布は完全なピラミッド型である.
一方,\ 大きさ$n=8$のとき,\ $ X$の分布は正規分布のような教会のベル(釣鐘)型}になる.
これはたまたまではなく,\ 背景に確率論・統計学の\.{中}\.{心}に君臨する大定理}がある.
証明は高校範囲外なので,\ 高校生は概要を知っていればよい.
中心極限定理 母集団(平均$m}$,\ 標準偏差$σ}$)がどんな分布であっても(注1)},\ $n}$が十分に大きいとき,\
標本平均$ X=X_1+X_2+・・・+X_n}{n$は近似的に正規分布$N-.2zw}m,\ σ^2}{n$に従う. \\[-.8zh]
(注1) 例外もあるが,\ 高校生は気にしなくてもよい.}
(注2) 標本平均$ X$の平均と標準偏差は,\ それぞれ$E( X)=m,\ \ σ( X)=σ}{√ n$であった.}
ヒストグラムは,\ 確率が柱の面積と等しくなる}ように作成している.\ 当然,\ 全柱の面積和は1である.
nが大きくなるほど標本平均\, X\,の分布が母平均2の近くに密集していく様子もわかる(大数の法則).
母集団がどんな変な分布であってもその標本の平均が正規分布に従うことには驚嘆せざるを得ない.
上例のように,\ nが比較的小さくても正規分布にかなり近くなる.
$なお,\ 母集団が正規分布N(m,\ σ^2)に従うとき,\ X\,はnが小さくても正規分布N-.2zw}m,\ σ^2}{n}に従う.}$
10000人の受験生が受けた模試の得点の平均は60点,\ 標準偏差は25点であった.
(1)\ \ 無作為に36人を選ぶとき,\ 36人の得点の平均$ X$が55点以上65点以下となる
確率と70点以上となる確率を求めよ.
(2)\ \ 無作為に100人を選ぶとき,\ 100人の得点の平均$ X$が55点以上65点以下と
なる確率を求めよ.
(3)\ \ 無作為に$n$人を選ぶとき,\ $n$人の得点の平均$ X$が58点以上62点以下となる
確率が0.95以上となる$n$の最小値を求めよ. \\
母集団や標本の大きさが小さくて近似できない問題は出題されないと考えてよい.
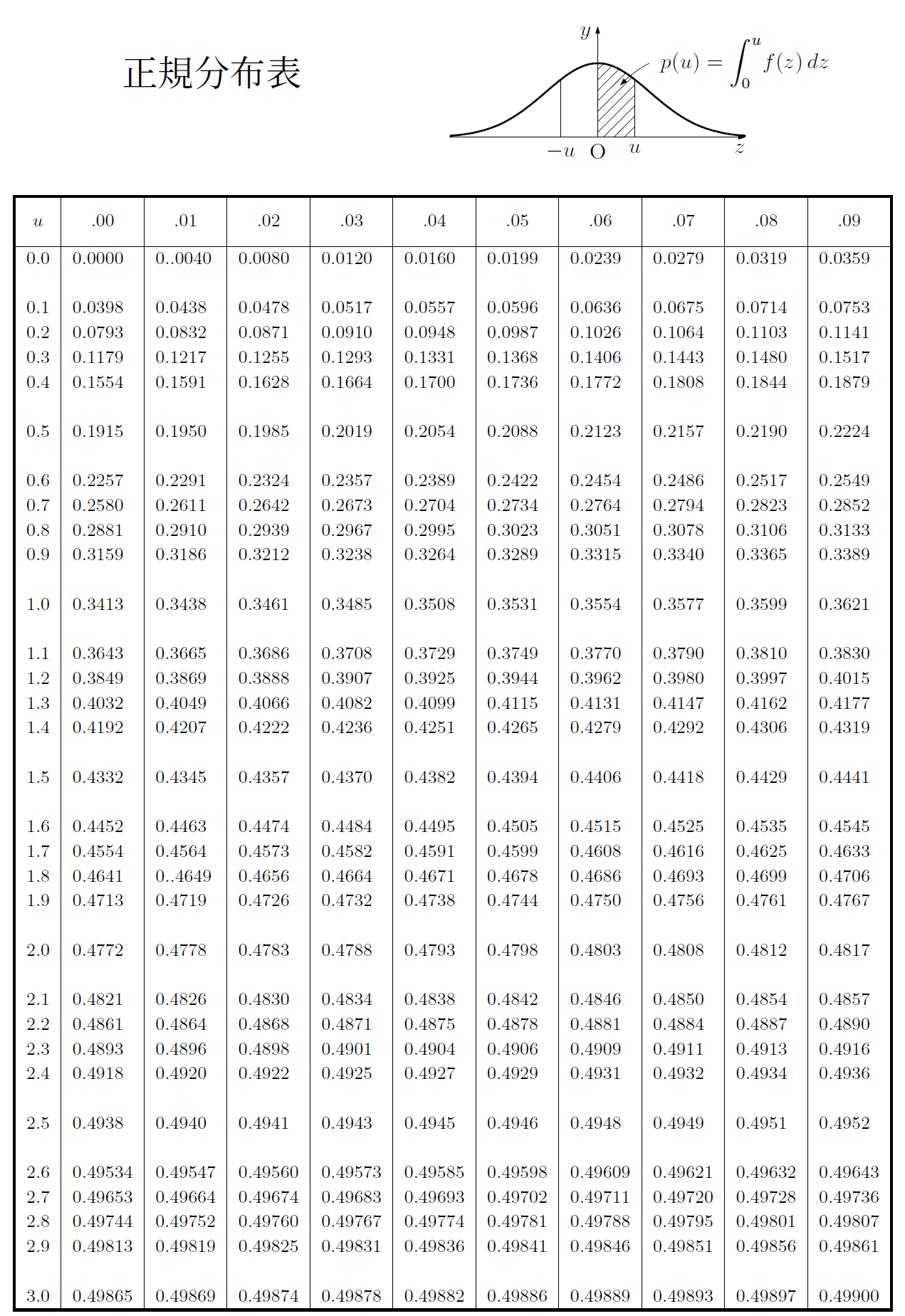
例によって,\ 正規分布は標準正規分布に変換し,\ 正規分布表を利用する.}
Xが平均m,\ 標準偏差\,σ\,の正規分布N(m,\ σ^2)に従うとする.
このとき,\ Z=X-m}{σ\,とおくと,\ Zは標準正規分布N(0,\ 1)に従うのであった.
(2)\ \ 標本が大きくなると,\ X\,が母平均60点に近い値をとる確率が高くなる(大数の法則).

