仮説検定の考え方は前項の「母平均の仮説検定」で解説済みである.
「母比率の仮説検定」のため,\ まず学習済みの標本比率の分布についての要点を再確認する.
特性Aの母比率$p$の母集団から大きさ$n$の無作為標本を抽出する.
標本の中で特性Aをもつ要素の個数をX}とすると,\ 標本比率$R$は\ \ $R= Xn}$
$X}$は二項分布$B(n,\ p)}$に従うから 平均$E(X)=np,\ \ 分散V(X)=np(1-p)$
よって,\ $n}$が大きいとき,\ $X}$は近似的に正規分布$N(np,\ np(1-p))}$に従う
標本調査では母集団が十分に大きく,\ 標本は復元抽出(反復試行)で作ると考えてよい.
確率pの試行をn回行うことになるから,\ 特性 Aをもつ要素の個数Xは二項分布B(n,\ p)に従う.
nが大きいとき,\ 二項分布(平均m=np,\ 分散\,σ^2=np(1-p))は正規分布N(m,\ σ^2)で近似できる.
Xが正規分布に従うとき,\ これを\,1n\,倍しただけの標本比率R= Xn\,も正規分布に従う.
確率変数の変換公式 E(aX+b)=aE(X)+b,\ \ V(aX+b)=a^2V(X)
ある1個のサイコロを180回振ったところ,\ 1の目が40回出た.\ このサイコロの1の目
が出る確率$p$は$16$ではないと判断してよいか.\ 有意水準5\%と有意水準1\%で検定せよ.対立仮説H$_1$を「1の目が出る確率は$16$ではない」}とする.
帰無仮説H$_0$を「1の目が出る確率は$16$である」}とする.
仮説$H_0$の元で,\ 1の目が出る回数Xは二項分布$B-.2zw}180,\ 16$に従う.
Xの平均\ $E(X)=180・16=30$ Xの標準偏差\
180回は十分に大きいから,\ Xは近似的に正規分布$N(30,\ 5^2)$に従う.
よって,\ $Z=X-30}{5}$は近似的に標準正規分布$N(0,\ 1)$に従う.
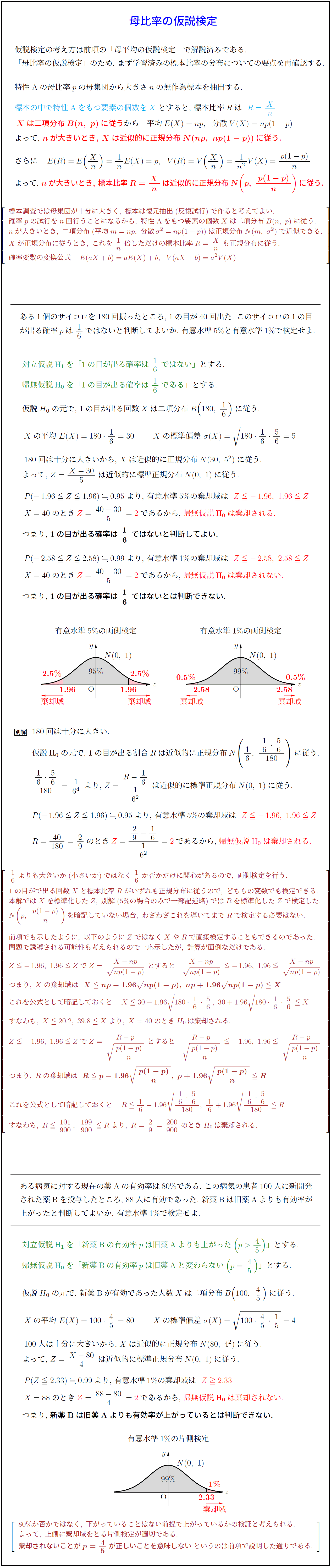
つまり,\ 1の目が出る確率は$16}$ではないと判断してよい.}
$P(-\,2.58≦ Z≦2.58)≒0.99$より,\ 有意水準1\%の棄却域は\ \ $Z≦-\,2.58,\ 2.58≦ Z}$
$X=40$のとき$Z}=40-30}{5}=2}$であるから,\ 帰無仮説H$_0$は棄却されない.}
つまり,\ 1の目が出る確率は$16}$ではないとは判断できない.}
180回は十分に大きい. \\
仮説H$_0$の元で,\ 1の目が出る割合$R$は近似的に正規分布 16\,よりも大きいか(小さいか)ではなく\,16\,か否かだけに関心があるので,\ 両側検定を行う.
1の目がで出る回数Xと標本比率Rがいずれも正規分布に従うので,\ どちらの変数でも検定できる.
本解ではXを標準化したZ,\ 別解(5\%の場合のみで一部記述略)ではRを標準化したZで検定した.
N-.2zw}p,\ p(1-p)}{n}を暗記していない場合,\ わざわざこれを導いてまでRで検定する必要はない.
前項でも示したように,\ 以下のようにZではなくXやRで直接検定することもできるのであった.
問題で誘導される可能性も考えられるので一応示したが,\ 計算が面倒なだけである.
ある病気に対する現在の薬Aの有効率は80\%である.\ この病気の患者100人に新開発
された薬Bを投与したところ,\ 88人に有効であった.\ 新薬Bは旧薬Aよりも有効率が
上がったと判断してよいか.\ 有意水準1\%で検定せよ. \\
対立仮説H$_1$を「新薬Bの有効率$p$は旧薬Aよりも上がった$p>45$」}とする.
帰無仮説H$_0$を「新薬Bの有効率$p$は旧薬Aと変わらない$p=45$」}とする. \\
仮説$H_0$の元で,\ 新薬Bが有効であった人数Xは二項分布$B-.2zw}100,\ 45$に従う.
100人は十分に大きいから,\ Xは近似的に正規分布$N(80,\ 4^2)$に従う.
よって,\ $Z=X-80}{4}$は近似的に標準正規分布$N(0,\ 1)$に従う.
$P(Z≦2.33)≒0.99$より,\ 有意水準1\%の棄却域は\ \ $Z≧2.33}$
$X=88$のとき$Z}=88-80}{4}=2}$であるから,\ 帰無仮説H$_0$は棄却されない.}
つまり,\ 新薬Bは旧薬Aよりも有効率が上がっているとは判断できない.}
80\%か否かではなく,\ 下がっていることはない前提で上がっているかの検証と考えられる.
よって,\ 上側に棄却域をとる片側検定が適切である.
棄却されないことがp=45\,が正しいことを意味しない}というのは前項で説明した通りである.

